A Concise Introduction to Logic

8.1 a historical example

dans son livre, The Two New Sciences, Galileo Galilea (1564-1642) donne plusieurs arguments destinés à démontrer qu’il ne peut y avoir une telle chose que les infinis réels ou infinitésimaux réels. Un de ses arguments peut être reconstruit de la manière suivante. Galileo propose que nous prenons comme postulat qu’il est en réalité une infinité de nombres naturels (les nombres naturels sont les nombres entiers de 1 sur):

{1, 2, 3, 4, 5, 6, 7, ….,}

Il propose également que nous prenons comme postulat qu’il existe une infinité réelle des carrés des nombres naturels.

{1, 4, 9, 16, 25, 36, 49, ….}

maintenant, raisons Galileo, notez que ces deux groupes (aujourd’hui nous les appellerions « ensembles”) ont la même taille. Nous pouvons voir ce que nous pouvons voir qu’il y a une correspondance entre les deux groupes.,

{1,	2,	3,	4,	5,	6,	7, ….,div>
{1,	4,	9,	16,	25,	36,	49, …}

Si l’on peut associer à chaque nombre naturel avec un et un seul nombre carré, et si l’on peut associer à chaque nombre carré avec un et un seul nombre naturel, ces jeux doivent être de la même taille.,

mais attendez un instant, dit Galileo. Il y a évidemment beaucoup plus de nombres naturels qu’il n’y a de nombres carrés. C’est, chaque nombre carré est dans la liste des nombres naturels, mais beaucoup de nombres naturels ne sont pas dans la liste des nombres carrés. Les numéros suivants sont tous dans la liste des nombres naturels, mais pas dans la liste des nombres carrés.

{2, 3, 5, 6, 7, 8, 10, ….,}

donc, raisons Galileo, s’il y a beaucoup de nombres dans le groupe des nombres naturels qui ne sont pas dans le groupe des nombres carrés, et s’il n’y a pas de nombres dans le groupe des nombres carrés qui ne sont pas dans les nombres naturels, alors les nombres naturels est plus grand que les nombres carrés. Et si le groupe des nombres naturels est plus grand que le groupe des nombres carrés, alors les nombres naturels et les nombres carrés ne sont pas de la même taille.,

Nous avons atteint deux conclusions: l’ensemble des nombres naturels et l’ensemble des nombres carrés sont de la même taille; et, l’ensemble des nombres naturels et l’ensemble des nombres carrés ne sont pas de la même taille. C’est contradictoire.

Galileo soutient que la raison pour laquelle nous sommes arrivés à une contradiction est parce que nous avons supposé qu’il y a des infinis réels. Il conclut donc qu’il n’y a pas d’infinis réels.

8.2 preuves indirectes

notre logique n’est pas encore assez forte pour prouver quelques arguments valides. Considérez l’argument suivant comme exemple.,

(P→(QvR))

Q

R

P

Cet argument est valide. Par la première prémisse que nous savons: Si P étaient vrais, alors serait (Q v R) être vrai. Mais alors Q ou R ou les deux seraient vrais. Et par les deuxième et troisième prémisses, nous savons: Q est faux et R est faux. Il ne peut donc pas être que (Q v R) est vrai, et il ne peut donc pas être que P est vrai.

nous pouvons vérifier l’argument en utilisant une table de vérité. Notre table sera complexe parce que l’une de nos prémisses est complexe.,

T F T F T T F T T F F T T T T F T F F F F T T T T

In any kind of situation in which all the premises are true, the conclusion is true., Autrement dit: les prémisses ne sont vraies que dans la dernière rangée. Pour cette rangée, la conclusion est également vraie. Donc, c’est un argument valable.

mais prenez une minute et essayez de prouver cet argument. Nous commençons avec

Et maintenant, nous nous sommes arrêtés. Nous ne pouvons appliquer aucune de nos règles. Voici un argument valable que nous n’avons pas rendu notre système de raisonnement assez fort pour le prouver.

Il y a plusieurs façons de corriger ce problème et de rendre notre système de raisonnement assez fort., L’une des solutions les plus anciennes consiste à introduire une nouvelle méthode de preuve, traditionnellement appelée « reductio ad absurdum”, ce qui signifie une réduction à l’absurdité. Cette méthode est aussi souvent appelée « preuve indirecte”ou « dérivation indirecte ».

l’idée est que nous assumons le déni de notre conclusion, puis montrons qu’une contradiction en résulte. Une contradiction est montrée lorsque nous prouvons une phrase Ψ, et sa négation Ψ. Ce peut être n’importe quelle phrase. Le fait est que, compte tenu du principe de la bivalence, nous devons avoir prouvé quelque chose de faux. Si Ψ est vraie, alors Ψ est faux; et si Ψ est vraie, alors Ψ est faux., Nous n’avons pas besoin de savoir ce qui est faux (Ψ ou Ψ); il suffit de savoir que l’un d’eux doit être.

rappelez-vous que nous avons construit notre système logique afin qu’il ne puisse pas produire un mensonge à partir de déclarations vraies. La source du mensonge que nous produisons dans la dérivation indirecte doit donc être un mensonge que nous avons ajouté à notre argument. Et ce que nous avons ajouté à notre argument est le déni de la conclusion. Ainsi, la conclusion doit être vraie.,

La forme de l’argument, c’est comme ceci:

Traditionnellement, l’hypothèse indirecte de dérivation a également été communément appelé « l’hypothèse de reductio”.

à titre d’exemple concret, nous pouvons prouver notre cas perplexe.

Nous avons supposé que la négation de notre conclusion sur la ligne 4. La conclusion que nous pensions correcte était P, et le déni de ceci est P. à la ligne 7, Nous avons prouvé R., Techniquement, nous avons terminé à ce stade, mais nous aimerions être gentils avec quiconque essaie de comprendre notre preuve, alors nous répétons la ligne 3 afin que les phrases R et R soient côte à côte, et il est très facile de voir que quelque chose a mal tourné. Autrement dit, si nous avons prouvé à la fois R et R, alors nous avons prouvé quelque chose de faux.

notre raisonnement va maintenant comme ceci. Quel est le problème? La ligne 8 est une utilisation correcte de la répétition; la ligne 7 vient d’une utilisation correcte de modus tollendo ponens; la ligne 6 de la bonne utilisation du modus ponens; ligne 5 de l’utilisation correcte de la double négation., Donc, nous n’avons pas fait d’erreur dans notre raisonnement. Nous avons utilisé les lignes 1, 2 et 3, mais ce sont des prémisses que nous avons accepté de supposer correctes. Cela laisse la ligne 4. Cela doit être la source de ma contradiction. Il doit être fausse. Si la ligne 4 est fausse, alors P est vrai.

certaines personnes considèrent les preuves indirectes moins fortes que les preuves directes. Il existe de nombreuses et complexes, les raisons de cela. Mais, pour notre logique propositionnelle, aucune de ces raisons ne s’applique. En effet, il est possible de prouver que notre logique propositionnelle est cohérente., Cela signifie, il est possible de prouver que notre logique propositionnelle ne peut pas prouver un mensonge à moins que l’on introduit d’abord un mensonge dans le système. (Il n’est généralement pas possible de prouver que des systèmes logiques ou mathématiques plus puissants et avancés sont cohérents, de l’intérieur de ces systèmes; par exemple, on ne peut pas prouver en arithmétique que l’arithmétique est cohérente.) Étant donné que nous pouvons être certains de la cohérence de la logique propositionnelle, nous pouvons être certains que, dans notre logique propositionnelle une preuve indirecte est une bonne forme de raisonnement., Nous savons que si nous prouvons un mensonge, nous devons avoir mis un mensonge; et si nous sommes confiants sur toutes les autres hypothèses (c’est-à-dire les prémisses) de notre preuve à l’exception de l’hypothèse de dérivation indirecte, alors nous pouvons être convaincus que cette hypothèse de dérivation indirecte doit être la source du mensonge.

une note sur la terminologie est requise ici. Le mot « contradiction” est utilisé de manière ambiguë dans la plupart des discussions logiques. Cela peut signifier une situation comme nous le voyons ci-dessus, où deux phrases sont affirmées, et ces phrases ne peuvent pas toutes les deux être vraies., Ou cela peut signifier une seule phrase qui ne peut pas être vraie. Un exemple d’une telle phrase est (P^P)., La table de vérité pour cette phrase est:

ainsi, ce genre de phrase ne peut jamais être vrai, quelle que soit la signification de P.,

pour éviter toute ambiguïté, dans ce texte, nous appellerons toujours une phrase unique qui ne peut pas être vraie une « phrase contradictoire”. Ainsi, (P^P) est une phrase contradictoire. Les Situations où deux phrases sont affirmées qui ne peuvent pas toutes les deux être vraies seront appelées une « contradiction ».

8.3 notre exemple, et d’autres exemples

Nous pouvons reconstruire une version de L’argument de Galileo maintenant. Nous utiliserons la clé suivante.

P: Il y a des infinis réels (y compris les nombres naturels et les nombres carrés).,

Q: Il y a une correspondance un à un entre les nombres naturels et les nombres carrés.

R: La taille de l’ensemble des nombres naturels et de la taille de l’ensemble des nombres carrés sont les mêmes.

S: Tous les nombres carrés sont des nombres naturels.

T: certains nombres naturels ne sont pas des nombres carrés.

U: il y a plus de nombres naturels que de nombres carrés.,

Avec cette clé, l’argument sera traduit:

(p→Q)

(Q→R)

(P→(S^T))

((S^T)→U)

(U→r)

p

et nous pouvons prouver qu’il s’agit d’un argument valide en utilisant la dérivation indirecte:

sur la ligne 6, Nous avons supposé P parce que Galileo croyait que p et visait à prouver que P. C’est-à-dire Qu’il croyait Qu’il N’y avait pas d’infinis réels, et a donc supposé qu’il était faux de croire que ce Ce mensonge conduira à d’autres mensonges, s’exposant.,

pour ceux qui sont intéressés: Galilée a conclu qu’il n’y a pas d’infinis réels mais qu’il y a des infinis potentiels. Ainsi, a-t-il raisonné, ce n’est pas le cas que tous les nombres naturels existent (dans un certain sens d ‘ « exister”), mais il est vrai que vous pourriez compter les nombres naturels pour toujours. De nombreux philosophes avant et après Galilée ont tenu ce point de vue; il est similaire à un point de vue tenu par Aristote, qui était un logicien important et philosophe écrit près de deux mille ans avant Galilée.,

notez que dans un argument comme celui-ci, vous pourriez penser que ce n’est pas l’hypothèse de la dérivation indirecte, mais plutôt l’une des prémisses était la source de la contradiction. Aujourd’hui, la plupart des mathématiciens croient cela à propos de L’argument de Galilée. Un logicien et mathématicien nommé Georg Cantor (1845-1918), l’inventeur de la théorie des ensembles, a soutenu que les ensembles infinis peuvent avoir des sous-ensembles appropriés de la même taille., Autrement dit, Cantor a nié la prémisse 4 ci-dessus: même si tous les nombres carrés sont des nombres naturels, et tous les nombres naturels ne sont pas des nombres carrés, il n’est pas vrai que ces deux ensembles sont de taille différente. Cantor accepté cependant prémisse 2 ci-dessus, et, par conséquent, estimé que la taille de l’ensemble des nombres naturels et de la taille de l’ensemble des nombres carrés est le même. Aujourd’hui, en utilisant le raisonnement de Cantor, les mathématiciens et les logiciens étudient l’infini et ont développé un grand nombre de connaissances sur la nature de l’infini. Si cela vous intéresse, consultez la section 17.5.,

considérons un autre exemple pour illustrer la dérivation indirecte. Un ensemble très utile de théorèmes est aujourd’hui appelé « théorèmes de Morgan”, d’après le logicien Augustus De Morgan (1806-1871). Nous ne pouvons pas les énoncer complètement avant le chapitre 9, mais nous pouvons énoncer leur équivalent en anglais: DeMorgan a observé que (PvQ) et (P^Q) sont équivalents, et aussi que (P^Q) et (PvQ) sont équivalents. Compte tenu de cela, il devrait s’agir d’un théorème de notre langage qui ((PvQ)→(P^Q)). Nous allons le prouver.

la formule entière est conditionnelle, nous allons donc utiliser une dérivation conditionnelle., Notre preuve doit donc commencer:

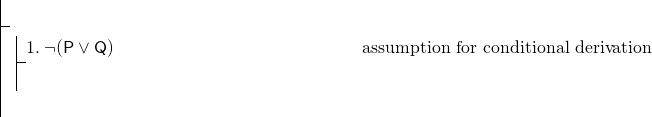
pour compléter la dérivation conditionnelle, il faut prouver (P^Q). C’est une conjonction, et notre règle pour montrer conjonctions est contiguïté. Puisque l’utilisation de cette règle pourrait être notre meilleur moyen de montrer (P^Q), Nous pouvons viser à montrer P, puis à montrer Q, Puis à effectuer une adjonction. Mais, nous avons évidemment très peu à travailler—juste la ligne 1, ce qui est une négation. Dans un tel cas, il est généralement sage de tenter une preuve indirecte. Commencez par une preuve indirecte de P.,

Nous avons maintenant besoin de trouver une contradiction—contradiction. Mais il y en a déjà une évidente. La ligne 1 dit que Ni P ni Q n’est vrai. Mais la ligne 3 dit que P est vrai. Nous devons rendre cette contradiction explicite en trouvant une formule et son déni. Nous pouvons le faire en utilisant addition.

Pour terminer la preuve, on utilise cette stratégie à nouveau.

Nous allons prouver les théorèmes De De Morgan, comme des problèmes pour le chapitre 9.,

Voici une règle générale pour faire des preuves: lorsque vous prouvez un conditionnel, faites toujours une dérivation conditionnelle; sinon, essayez la dérivation directe; si cela échoue, essayez la dérivation indirecte.

8.4 Problèmes

1. Toutes les preuves suivantes. Chacun nécessitera une dérivation indirecte. Les deux derniers sont difficiles.

1. Prouver les éléments suivants sont des théorèmes.

1. (P^P).
2. ((P→P)^(P→P)).
3. (P→(P^Q)).
4. ((P^Q)→(P→Q)).

1. en anglais familier normal, écrivez votre propre argument valide avec au moins deux prémisses., Votre argument ne devrait être qu’un paragraphe (pas une liste ordonnée de phrases ou toute autre chose qui ressemble à une logique formelle). Traduisez – le en logique propositionnelle et prouvez qu’il est valide en utilisant une dérivation indirecte.