Content

Fonctions de densité de probabilité

la fonction de densité de probabilité (pdf) \(f(x)\) d’une variable aléatoire continue \(X\) est définie comme la dérivée de la cdf \(F(x)\):

\

Il est parfois utile de considérer la cdf \(F(x)\) en termes)\):

\

le PDF\(F(X)\) a deux propriétés importantes:

1. \ (F(x) \geq 0\), pour tous\ (x\)
2. \(\displaystyle\int_ {- \infty}^{\infty} f(x)\; dx = 1\).,

une variété infinie de formes est possible pour un pdf, car les seules exigences sont les deux propriétés ci-dessus. Le pdf peut avoir un ou plusieurs pics, ou pas de pics du tout; il peut avoir des discontinuités, être composé de combinaisons de fonctions, etc. la figure 5 montre un pdf avec un seul pic et une légère asymétrie. Comme c’est le cas pour un pdf typique, la valeur de la fonction approche zéro comme \(x \to \infty\) et \(x \to -\infty\).

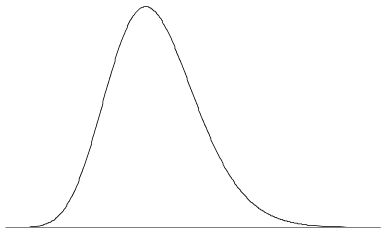
Figure 5: un pdf peut ressembler à ceci.,

nous explorons maintenant comment les probabilités concernant la variable aléatoire continue \(X\) se rapportent à son pdf. Le résultat important ici est que

\_a^B.\]

Ce résultat découle du fait que les deux côtés sont égaux à \(F(b) – F(a)\).

Notes.

• Pour une variable aléatoire continue, nous devons considérer la probabilité qu’il se trouve dans un intervalle. L’importance de ce résultat est qu’il nous dit que, pour trouver la probabilité, nous avons besoin de trouver l’aire sous la pdf sur l’intervalle donné.
• la surface totale sous le pdf est égale à 1., Donc, ce résultat nous dit que, pour approximer la probabilité que la variable aléatoire se trouve dans un intervalle donné, il suffit de deviner la fraction de la zone sous le pdf entre les extrémités de l’intervalle.
• ce résultat fournit une autre perspective sur la raison pour laquelle les PDF ne peuvent pas être négatifs, car s’ils l’étaient, une probabilité négative pourrait être obtenue, ce qui est impossible.
• le pdf est analogue à, mais différent de, la fonction de probabilité (PF) pour une variable aléatoire discrète. Un pf donne une probabilité, il ne peut donc pas être supérieur à un., Un pdf \(f(x)\), cependant, peut donner une valeur supérieure à un pour certaines valeurs de \(x\), car elle n’est pas la valeur de \(f(x)\), mais l’aire sous la courbe qui représente la probabilité. D’autre part, la hauteur de la courbe reflète la probabilité relative. Si \(f(b) = 2f(a)\), puis une observation près de \(b\) est environ deux fois plus susceptibles que d’une observation près de \(a\).,

page Suivante – le Contenu – la Moyenne et la variance d’une variable aléatoire continue