En regressionsmodel for Overlevelse Data
jeg har tidligere skrevet om, hvordan til at beregne Kaplan–Meier-kurve for overlevelse data. Som en ikke-parametrisk estimator gør det et godt stykke arbejde med at give et hurtigt kig på overlevelseskurven for et datasæt. Men hvad det ikke lader dig gøre er at modellere virkningen af kovariater på overlevelse. I denne artikel fokuserer vi på co.Proportional Ha .ards-modellen, en af de mest anvendte modeller til overlevelsesdata.
Vi går i dybden med, hvordan vi beregner estimaterne., Dette er værdifuldt, fordi vi vil se, at estimaterne kun afhænger af bestilling af fejl og ikke deres faktiske tider. Vi vil også kort diskutere nogle vanskelige spørgsmål om årsagssammenhæng, der er specielle for overlevelsesanalyse.
Vi tænker typisk på overlevelsesdata med hensyn til overlevelseskurver som den nedenfor.,
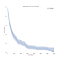
På x-aksen, vi har tid i dage. På y-aksen har vi (en estimator for) procentdelen (teknisk, andelen) af emner i befolkningen, der “overlever” til den tid. Overlev kan være figurativ eller bogstavelig., Det kan være, om folk lever i en bestemt alder, om en maskine gør det til en vis tid uden at bryde sammen, eller det kan være, om nogen forbliver arbejdsløs en vis tid efter at have mistet deres job.
af afgørende betydning er komplikationen i overlevelsesanalyse, at nogle forsøgspersoner ikke har deres “død” observeret. De kan stadig være i LIVE, en maskine kan stadig fungere, eller nogen kan stadig være arbejdsløse på det tidspunkt, dataene indsamles., Sådanne observationer kaldes “retcensureret”, og håndtering af censur betyder, at overlevelsesanalyse kræver forskellige statistiske værktøjer.
vi betegner overlevelsesfunktionen som s, en funktion af tiden. Dens output er procentdelen af emner, der overlever på tidspunktet t. (igen er det teknisk set en andel mellem 0 og 1, men jeg vil bruge de to ord om hverandre). For enkelhedens skyld vil vi antage den tekniske antagelse, at hvis vi venter længe nok, vil alle emner “dø.”
Vi indekserer emnerne med et abonnement som i eller j., Den manglende gange af hele befolkningen vil være angivet med et lignende indeks, der på det tidspunkt variabel t.

En anden underfundighed til at overveje, er, om vi behandler tid som diskrete (uge efter uge, for eksempel) eller løbende. Filosofisk set måler vi kun tid i diskrete trin (til nærmeste sekund, siger)., Normalt vil vores data kun fortælle os, om nogen døde i et givet år, eller hvis en maskine mislykkedes på en given dag. Jeg vil gå frem og tilbage mellem de diskrete og kontinuerlige sager for at holde udstillingen så klar som muligt.
Når vi forsøger at modellere virkningerne af kovariater (f.eks. alder, køn, race, maskinproducent), vil vi typisk være interesseret i at forstå effekten af kovariatet på Farehastigheden. Farehastigheden er den øjeblikkelige Sandsynlighed for fiasko/død/tilstandsovergang på et givet tidspunkt t, betinget af allerede at have overlevet så længe., Vi vil betegne det λ (t). Behandling tid som diskrete:
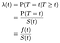
Hvor f er den overordnede sandsynlighed for tæthed af mangel på tid t. Vi kan forene de diskrete og kontinuerte tilfælde ved at lade delta funktioner i probability density “funktion”. Resultatet λ = F / S er således det samme for den kontinuerlige sag.
lad os rette et eksempel., Lad os overveje sammenhængen i et klinisk forsøg, hvor et lægemiddel oprindeligt får en sygdom til at gå i remission. Vi vil sige, at stoffet “fejler” for et emne, når sygdommen begynder at udvikle sig for et emne. Antag endelig, at individers sygdomsstatus måles hver uge. Så hvis λ(3) = 0.1, betyder det, at der er en 10% chance for, at for et givet individ, hvis de stadig er i remission før uge 3, vil deres sygdom begynde at udvikle sig i uge 3. De øvrige 90% vil forblive i remission.,
dernæst er den samlede sandsynlighedsdensitetsfunktion f kun derivatet af S med hensyn til tid. (Igen, hvis tiden er diskret, er f bare summen af nogle delta-funktioner).,341fa8b2″>
Dette betyder, at hvis vi kender Faren funktion, kan vi løse denne differentialligning for S:
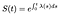
Hvis tiden er diskret, integreret i en sum af delta funktioner, der bare bliver til en sum af de farer, der er ved hver diskret tid.,
Okay, der opsummerer notation og grundlæggende begreber, som vi får brug for. Lad os gå videre til at diskutere modeller.
ikke-, Semi-og fuldt parametriske modeller
som jeg sagde tidligere, er vi typisk interesserede i at modellere Farehastigheden..
i en ikke-parametrisk model gør vi ingen antagelser om den funktionelle form for λ. Kaplan-Meier-kurven er den maksimale Sandsynlighedsestimator i dette tilfælde. Ulempen er, at dette gør det svært at modellere nogen virkninger af kovariater. Det er lidt som at bruge et scatter plot for at forstå effekten af en kovariat., Ikke nødvendigvis så nyttigt som en fuldt parametrisk model som en lineær regression.
i en fuldt parametrisk model antager vi den præcise funktionelle form for λ. En diskussion af de fuldt parametriske modeller er en hel artikel i sig selv, men det er værd at en meget kort diskussion. Tabellen nedenfor viser tre af de mest almindelige fuldt parametriske modeller. Hver generaliseres af den næste, der går fra 1 til 2 til 3 parametre. Den funktionelle form for farefunktionen er vist i den midterste kolonne. Logaritmen til farefunktionen vises også i den sidste kolonne., Alle parametre (,,,, μ) antages at være positive, bortset fra AT μ kunne være 0 i den generaliserede distributioneibull distribution (gengiver distributioneibull distribution).

Ser man på logaritmen viser os, at den eksponentielle model forudsætter, at den fare funktion er konstant. Modeleibull-modellen antager, at det øges, hvis
problemet med disse modeller er, at de gør stærke antagelser om dataene. I visse sammenhænge kan der være grund til at tro, at disse modeller passer godt. Men med disse og flere andre tilgængelige muligheder er der en stærk risiko for at drage forkerte konklusioner på grund af forkert specifikation af modellen.
Dette er grunden til co.Proportional farer, en semi-parametrisk model er så populær., Der foretages ingen funktionelle antagelser om formen på Farefunktionen; i stedet, antagelser i funktionel form foretages om virkningerne af kovariaterne alene.,
Cox Proportional Hazards Model
Cox Proportional Hazards Model er normalt gives i form af den tid t, covariate vektor x, og koefficienten vektor β som
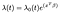
hvor λₒ er en vilkårlig funktion af tiden, baseline hazard. Dot produkt af and og β er taget i eksponenten ligesom i standard lineær regression., Uanset værdierne kovariater, alle forsøgspersoner deler den samme baseline fare λ.. Derefter foretages justeringer baseret på kovariaterne.
Fortolkning af Resultater
Antag, for i det øjeblik, at vi har det passer en Cox Proportional Hazards model til vores data, som bestod af
- En kolonne med angivelse af tidspunktet for hvert emne
- En kolonne med angivelse af, om emnet var “observeret” (at have fejlet, eller, i vores foretrukne eksempel, for at få deres sygdom fremskridt). En værdi på 1 betyder, at individet havde deres sygdomsforløb., En værdi på 0 betyder, at sygdommen på det sidste observationstidspunkt ikke var kommet frem. Observationen blev censureret.
- kolonner til vores kovariater..
efter pasformen får vi værdier for β. Antag for eksempel for enkelhed, at der er en enkelt kovariat. En værdi af β=0,1 betyder, at en stigning i kovariatet med en mængde på 1 fører til en cirka 10% høj chance for sygdomsprogression på et givet tidspunkt., Den nøjagtige værdi er i virkeligheden

For små værdier af β, den værdi af β i sig selv er en ganske god tilnærmelse til det eksakte stigning i fare. For Større værdier af β skal det nøjagtige beløb beregnes.
en anden måde at udtrykke β=0, 1 er, at når hazard øges, øges faren med en hastighed på 10% pr. Den større 10.,52% stammer fra (kontinuerlig) sammensætning, ligesom med sammensat rente.
også β=0 betyder ingen effekt, og β-negativ betyder, at der er mindre risiko, da kovariatet øges. Bemærk, at der i modsætning til i standardregressioner ikke er nogen aflytningsperiode. I stedet absorberes interceptet i basisfaren λₒ, som også kan estimeres (se nedenfor).
endelig, hvis vi antager, at vi har estimeret baseline ha .ard-funktionen, kan vi konstruere survivor-funktionen.,
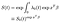
Den hidtidige funktion er opløftet til en potens af exp(xʹß) faktor, der kommer fra kovariater. Der skal udvises en vis omhu ved fortolkningen af baseline survivor-funktionen, som groft spiller rollen som intercept-udtrykket i en regelmæssig lineær regression. Hvis kovariaterne er blevet centreret (middel 0), repræsenterer den overlevelsesfunktionen for det “gennemsnitlige” emne.,
Estimering af Cox Proportional Hazards Model
I 1970’erne, David Cox, en Britisk matematiker, har foreslået en måde at estimere β uden at skulle estimere baseline hazard λₒ. Igen kan basisfaren estimeres bagefter. Som tidligere nævnt vil vi se, at det er rækkefølgen af de observerede fejl, der betyder noget, ikke tiderne selv.
før du hopper ind i estimatet, er det værd at diskutere bånd. Da vi typisk kun observerer data i diskrete trin, er det muligt, at der kan opstå to fejl på samme tid., For eksempel kan to maskiner mislykkes i samme uge, og optagelsen foretages kun ugentligt. Disse bånd gør analysen af situationen temmelig kompliceret uden at tilføje meget indsigt. Derfor vil jeg udlede estimaterne i tilfælde af ingen bånd.Husk, at vores data består af observationer af nogle talfejl på diskret tid. Lad R (t) betegne befolkningen “i fare” på tidspunktet t. Hvis et emne i vores undersøgelse har svigtet (sygdom skred frem, for eksempel) før tid t, de er ikke “i fare.,”Også, hvis et emne i vores undersøgelse har fået deres observation censureret på et tidspunkt før tid t, er de heller ikke “i fare.”
på den sædvanlige måde ønsker vi at konstruere en sandsynlighedsfunktion (hvad er sandsynligheden for, at vi ville have observeret de data, vi gjorde, i betragtning af kovariaterne og koefficienterne) og derefter optimere det for at få en estimator med maksimal sandsynlighed.
for hver diskret tid, hvor vi observerede en fejl i emne j, er sandsynligheden for, at der opstår, da der opstod en fejl, under. Summen overtages alle forsøgspersoner, der er i fare på tidspunktet j.,

Bemærk, at baseline hazard λₒ er faldet ud! Meget praktisk. Af denne grund er sandsynligheden for, at vi konstruerer, kun en delvis Sandsynlighed. Bemærk også, at tiderne slet ikke vises., Udtrykket for emne j afhænger kun af, hvilke emner der stadig lever på tidspunktet j, hvilket igen kun afhænger af den rækkefølge, hvor emnerne censureres eller observeres at mislykkes.
den delvise sandsynlighed er selvfølgelig kun produktet af disse vilkår, en for hver fejl, vi observerer (ingen vilkår for censurerede observationer).,
log delvis sandsynligheden er så
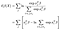
Det passer sker med standard numeriske metoder, for eksempel i python-pakke statsmodels og varians-kovarians matricen for de estimater, der er givet ved (reciprokke) Fisher Oplysninger Matrix. Intet spændende her.,
estimering af Baseline Survivor-funktionen
nu hvor vi har estimeret koefficienterne, kan vi estimere survivor-funktionen. Dette ender med at være meget lig at estimere en Kaplan-Meier-kurve.
Vi postulerer udtryk α indekseret af i. på tid i skal baseline survivor curve falde med en brøkdel α, der repræsenterer andelen af personer i fare, der fejler på tid i., Med andre ord
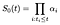
for At beregne den maksimale sandsynlighed for estimator for α, vi anser sandsynligheden bidrag fra emne, som jeg ikke ved jeg, og særskilt bidrag fra dem, der er censureret ved jeg.
For et emne, der ikke ved jeg, at den sandsynlighed er givet ved sandsynligheden for, at de er i live på tidspunktet jeg mindre sandsynlighed for, at de er i live på det næste gang i+1. (Vi antager midlertidigt, at tiderne er bestilt).,
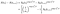
Hvis du i stedet, at de er censureret ved jeg, bidrag er lige sandsynligheden for, at de er i live på det tidspunkt, efter jeg, det vil sige at de ikke er døde endnu., Dette er blot
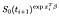
Der er en ekstra sigt fra de emner, der blev observeret (dvs observeret til at mislykkes, i stedet for at censureret)., Log sandsynlighed bliver
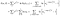
jeg har været lidt sjusket om at holde styr på endpoints (jeg vs. i+1), men det vil alle arbejde ud.
der er kun α-udtryk for emner, vi observerede at mislykkes., Differentierer med hensyn til j-j og antager ingen bånd, får vi et bidrag fra summen til venstre kun for emner, der lever på tidspunktet j, og et enkelt bidrag fra udtrykket til højre.,qual at 0 betyder, at vi kan opnå den maksimale sandsynlighed for estimater for α bruge vores skøn for β som løsningen på de mange ligninger, en for hvert emne, som blev observeret til at mislykkes:
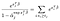
Udvidelser og Begrænsninger
Der er masser mere at sige om Cox Proportional Hazards modeller, men jeg vil prøve at holde det kort og bare nævne et par ting.,
for eksempel kan man overveje tidsvarierende regressorer, og det er muligt.
den anden afgørende ting at huske på er udeladt variabel bias. I standard lineær regression er udeladte variabler, der ikke er korreleret med regressorerne, ikke et stort problem. Dette er ikke sandt i overlevelsesanalyse. Antag, at vi har to lige store og samplede delpopulationer i vores data hver med en konstant farehastighed, den ene er 0.1 og den anden er 0.5. Oprindeligt vil vi se en høj farehastighed (gennemsnittet, kun 0, 3)., Som tiden går, vil befolkningen med en høj farehastighed forlade befolkningen, og vi vil observere en farehastighed, der falder mod 0.1. Hvis vi udelader variablen, der repræsenterer disse to populationer, vil vores baseline farehastighed være helt ødelagt.