8.1 Et historisk eksempel
I sin bog, De To Nye Videnskaber, Galileo Galilea (1564-1642) giver flere argumenter beregnet til at påvise, at der kan være sådan noget som faktiske infinities eller faktiske infinitesimals. Et af hans argumenter kan rekonstrueres på følgende måde. Galileo foreslår, at vi tager som en forudsætning, at der er en aktuel uendelighed af naturlige tal (de naturlige tal er det positive hele tal fra 1 til):
{1, 2, 3, 4, 5, 6, 7, ….,}
han foreslår også, at vi tager som en forudsætning, at der er en faktisk uendelighed af kvadraterne af de naturlige tal.
{1, 4, 9, 16, 25, 36, 49, ….}
nu, Galileo grunde, bemærk at disse to grupper (i dag ville vi kalde dem “sæt”) har samme størrelse. Vi kan se dette, fordi vi kan se, at der er en en-til-en korrespondance mellem de to grupper.,
| {1, | 2, | 3, | 4, | 5, | 6, | 7, ….,div> | |
| {1, | 4, | 9, | 16, | 25, | 36, | 49, …} |
Hvis vi kan knytte alle naturlige tal med én og kun én-pladsen tal, og hvis vi kan knytte hver kvadrat nummer med én og kun én naturligt tal, så er disse sæt skal være af samme størrelse.,
men vent et øjeblik, siger Galileo. Der er naturligvis meget mange flere naturlige tal, end der er firkantede tal. Det vil sige, hvert firkantet tal er på listen over naturlige tal, men mange af de naturlige tal er ikke på listen over firkantede tal. Følgende tal er alle på listen over naturlige tal, men ikke på listen over firkantede tal.
{2, 3, 5, 6, 7, 8, 10, ….,}
Så, Galileo grunde, hvis der er mange tal i gruppen af naturlige tal, der ikke er med i gruppen af pladsen numre, og hvis der er ingen tal i gruppen af pladsen numre, der ikke er i naturals numre, så de naturlige tal er større end kvadratisk tal. Og hvis gruppen af de naturlige tal er større end gruppen af de firkantede tal, så er de naturlige tal og de firkantede tal ikke af samme størrelse.,
Vi har nået to konklusioner: sæt af de naturlige tal og sæt af de firkantede tal er af samme størrelse; og sæt af de naturlige tal og sæt af de firkantede tal er ikke den samme størrelse. Det er selvmodsigende.
Galileo hævder, at grunden til, at vi nåede en modsigelse, er fordi vi antog, at der er faktiske uendeligheder. Han konkluderer derfor, at der ikke er nogen faktiske uendeligheder.
8.2 indirekte beviser
vores logik er endnu ikke stærk nok til at bevise nogle gyldige argumenter. Overvej følgende argument som et eksempel.,
(P→(QvR))
Q
R
P
Dette argument ser gyldigt. Ved den første forudsætning ved vi: hvis P var sandt, så ville det (v v R) være sandt. Men så ville enten Q eller R eller begge være sandt. Og ved det andet og tredje udgangspunkt kender vi: Q er falsk, og R er falsk. Så det kan ikke være, at (v v R) er sandt, og så det kan ikke være, at p er sandt.
Vi kan kontrollere argumentet ved hjælp af en sandhedstabel. Vores bord vil være kompleks, fordi en af vores forudsætninger er kompleks.,
In any kind of situation in which all the premises are true, the conclusion is true., Det vil sige: lokalerne er alle sande kun i sidste række. For den række er konklusionen også sand. Så dette er et gyldigt argument.
men tag et minut og prøv at bevise dette argument. Vi begynder med

og nu er vi stoppet. Vi kan ikke anvende nogen af vores regler. Her er et gyldigt argument om, at vi ikke har gjort vores ræsonnementssystem stærkt nok til at bevise.
Der er flere måder at rette op på dette problem og gøre vores ræsonnementssystem stærkt nok., En af de ældste løsninger er at introducere en ny bevismetode, traditionelt kaldet” reductio ad absurdum”, hvilket betyder en reduktion til absurditet. Denne metode kaldes også ofte et “indirekte bevis”eller” indirekte afledning”.
ideen er, at vi antager benægtelse af vores konklusion, og derefter viser, at en modsigelse resulterer. En modsigelse er vist, når vi bevise nogle sætning., og dens negation.. Dette kan være enhver sætning. Pointen er, at i betragtning af bivalensprincippet må vi have bevist noget falsk. For hvis.er sandt, så false er falsk, og hvis. er sandt, så false er falsk., Vi behøver ikke at vide, hvilket er falsk (Ψ Eller Ψ); det er nok at vide, at en af dem skal være.
Husk, at vi har bygget vores logiske system, så det ikke kan producere en løgn fra sande udsagn. Kilden til den løgn, som vi producerer i den indirekte afledning, må derfor være en løgn, som vi føjede til vores argument. Og hvad vi føjede til vores argument er benægtelse af konklusionen. Konklusionen skal således være sand.,
Den form for argumentation er ligesom dette:

Traditionelt formodning for indirekte udledning, er også blevet kaldet “den antagelse, for reductio”.
som et konkret eksempel kan vi bevise vores forvirrende sag.

vi antog afslag på vores konklusion på linje 4. Den konklusion, vi troede var korrekt, VAR P, og benægtelsen af dette er P. I linje 7, vi beviste R., Teknisk set, så er vi færdige på det tidspunkt, men vi vil gerne være sådan, at nogen prøver at forstå vores bevis, så vi gentager linje 3, således at sætninger R og R er side om side, og det er meget let at se, at noget er gået galt. Det vil sige, hvis vi har bevist både R og R, så har vi bevist noget falsk.
vores ræsonnement går nu sådan. Hvad gik galt? Linje 8 er en korrekt brug af gentagelse; line 7 kommer fra en korrekt brug af modus tollendo ponens; linje 6 fra en korrekt brug af modus ponens; linje 5 fra en korrekt anvendelse af dobbelt negation., Så vi begik ikke en fejl i vores ræsonnement. Vi brugte linjer 1, 2, og 3, men det er lokaler, som vi blev enige om at antage, er korrekte. Dette efterlader linje 4. Det må være kilden til min modsigelse. Det må være falsk. Hvis linje 4 er falsk, er P sand.nogle mennesker anser indirekte bevis mindre stærke end direkte bevis. Der er mange og komplekse grunde til dette. Men for vores propositionslogik gælder ingen af disse grunde. Dette skyldes, at det er muligt at bevise, at vores propositionslogik er konsistent., Det betyder, at det er muligt at bevise, at vores propositionslogik ikke kan bevise en løgn, medmindre man først introducerer en løgn i systemet. (Det er generelt ikke muligt at bevise, at mere kraftfulde og avancerede logiske eller matematiske systemer er konsistente inde fra disse systemer; for eksempel kan man ikke bevise i aritmetik, at aritmetik er konsistent.) I betragtning af at vi kan være sikre på konsistensen af propositionslogikken, kan vi være sikre på, at et indirekte bevis i vores propositionslogik er en god form for ræsonnement., Vi ved, at hvis vi beviser en løgn, må vi have lagt en løgn i; og hvis vi er sikre på alle de andre antagelser (det vil sige præmisserne) for vores bevis bortset fra antagelsen om indirekte afledning, så kan vi være sikre på, at denne antagelse om indirekte afledning skal være kilden til falskheden.
Der kræves en note om terminologi her. Ordet” modsigelse ” bliver brugt tvetydigt i de fleste logiske diskussioner. Det kan betyde en situation som vi ser ovenfor, hvor to sætninger hævdes, og disse sætninger kan ikke begge være sande., Eller det kan betyde en enkelt sætning, der ikke kan være sandt. Et eksempel på en sådan sætning er (p^p)., Sandhedstabellen for denne sætning er:
| S | S | (P ^ P) |
|---|---|---|
| T | F | F |
| F | T | F |
Således, at denne form for straf kan aldrig være sandt, uanset om betydningen af P.,
for at undgå tvetydighed vil vi i denne tekst altid kalde en enkelt sætning, der ikke kan være sandt, en “modstridende sætning”. Således er (p^p) en modstridende sætning. Situationer, hvor to sætninger hævdes, at begge ikke kan være sande, kaldes en “modsigelse”.
8.3 vores eksempel og andre eksempler
Vi kan rekonstruere en version af Galileos argument nu. Vi bruger følgende nøgle.
P: Der er faktiske infinities (herunder de naturlige tal og de firkantede tal).,
Q: der er en en-til-en korrespondance mellem de naturlige tal og de firkantede tal.
R: størrelsen af sættet af de naturlige tal og størrelsen af sættet af de firkantede tal er de samme.
s: alle de firkantede tal er naturlige tal.
T: nogle af de naturlige tal er ikke firkantede tal.
U: der er mere naturlige tal end firkantede tal.,
Med denne nøgle, det argument vil blive oversat:
(P→Q)
(Q→R)
(P→(S^T))
((S^T)→U)
(U→R)
P
Og vi kan bevise det er et gyldigt argument ved hjælp af indirekte udledning:

På linje 6, vi gik ud P, fordi Galileo troede, at S og havde til formål at bevise, at P. er, at han mente, at der er ingen egentlig infinities, og så ud fra, at det var forkert at tro, at det er ikke sådan, at der er ingen egentlig infinities. Denne løgn vil føre til andre usandheder, udsætter sig selv.,
for dem, der er interesseret: Galileo konkluderede, at der ikke er nogen faktiske uendeligheder, men der er potentielle uendeligheder. Således begrundede han, at det ikke er tilfældet, at alle de naturlige tal eksisterer (i en vis forstand “eksisterer”), men det er sandt, at du kunne tælle naturlige tal for evigt. Mange filosoffer før og efter Galileo holdt denne opfattelse, det svarer til en opfattelse indehaves af Aristoteles, der var en vigtig logician og filosof skriftligt næsten to tusinde år før Galileo.,
Bemærk, at i et argument som dette kan du begrunde, at ikke antagelsen om indirekte afledning, men snarere et af lokalerne var kilden til modsætningen. I dag tror de fleste matematikere dette om Galileos argument. En logiker og matematiker ved navn Georg Cantor (1845-1918), opfinderen af sætteori, argumenterede for, at uendelige sæt kan have ordentlige undergrupper af samme størrelse., Det er, Cantor benægtede forudsætning 4 ovenfor: selvom alle firkantede tal er naturlige tal, og ikke alle naturlige tal er firkantede tal, det er ikke tilfældet, at disse to sæt er af forskellig størrelse. Cantor accepterede dog forudsætning 2 ovenfor, og troede derfor, at størrelsen af sæt af naturlige tal og størrelsen af sæt af firkantede tal er den samme. I dag bruger Cantor ‘ s ræsonnement, matematikere og logicians undersøgelse uendeligt, og har udviklet en stor mængde viden om karakteren af uendelighed. Hvis dette interesserer dig, se afsnit 17.5.,
lad os overveje et andet eksempel for at illustrere indirekte afledning. Et meget nyttigt sæt af teoremer er i dag kaldes “De Morgan ‘ s teoremer”, efter logician Augustus De Morgan (1806-1871). Vi kan ikke angive disse fuldt ud indtil kapitel 9, men vi kan angive deres ækvivalent på engelsk: DeMorgan observerede, at (PV.) og (P^Q) er ækvivalente, og også at (P^and) og (PV.) er ækvivalente. I betragtning af dette bør det være en sætning af vores sprog, som ((PV.). (P^Q)). Lad os bevise det.
hele formlen er en betinget, så vi vil bruge en betinget afledning., Vores bevis skal således begynde:
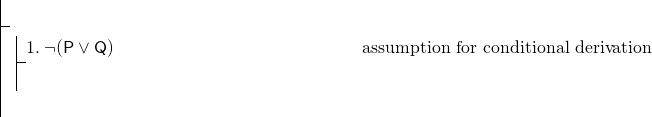
for at afslutte den betingede afledning skal vi bevise (P^Q). Dette er en sammenhæng, og vores regel for at vise konjunktioner er adjunktion. Da brug af denne regel kan være vores bedste måde at vise (P^)), kan vi sigte mod at vise P og derefter vise Q og derefter udføre adjunction. Men vi har selvfølgelig meget lidt at arbejde med-bare linje 1, hvilket er en negation. I et sådant tilfælde er det typisk klogt at forsøge et indirekte bevis. Start med et indirekte bevis på P.,

Vi skal nu finde en modsigelse—nogen modsætning. Men der er allerede en indlysende. Linje 1 siger, at hverken P eller Q er sandt. Men linje 3 siger, at P er sandt. Vi må gøre denne modsigelse eksplicit ved at finde en formel og dens benægtelse. Vi kan gøre dette ved hjælp af tilføjelse.

for at afslutte beviset bruger vi denne strategi igen.

Vi vil bevise, De Morgan ‘ s teoremer som problemer, til i kapitel 9.,
Her er en generel tommelfingerregel for at gøre beviser: når bevise en betinget, altid gøre betinget afledning; ellers, prøv direkte afledning; hvis det mislykkes, så prøv indirekte afledning.
8.4 problemer
- udfyld følgende beviser. Hver vil kræve en indirekte afledning. De sidste to er udfordrende.
- bevise følgende er teoremer.
- (p^p).
- ((p^p) ^ (p.p)).
- (p ((p^Q)).
- ((p^)) ((p.))).
- på normalt Engelsk Engelsk skal du skrive dit eget gyldige argument med mindst to lokaler., Dit argument skal bare være et afsnit (ikke en ordnet liste over sætninger eller noget andet, der ligner formel logik). Oversætte det til propositional logik og bevise det er gyldigt ved hjælp af en indirekte afledning.
denne oversættelse af titlen på Galileos bog er blevet den mest almindelige, Selv om en mere bogstavelig ville have været matematiske diskurser og demonstrationer. Oversættelser af bogen omfatter Drake (1974).