α-koefficienten er den mest udbredte procedure til at vurdere pålideligheden i anvendt forskning. Som anført af Sijtsma (2009) er dens popularitet sådan, at Cronbach (1951) er blevet nævnt som en reference oftere end artiklen om opdagelsen af DNA-dobbeltheli .en., Ikke desto mindre er dens begrænsninger velkendte (Lord and Novick, 1968; Cortina, 1993; Yang and Green, 2011), nogle af de vigtigste er antagelserne om ukorrelerede fejl, tau-ækvivalens og normalitet.
Den antagelse af ukorrelerede fejl (fejl score for ethvert par af elementer, der er ukorrelerede) er en hypotese om Klassisk Test Teori (Herren og Novick, 1968), overtrædelse af, som kan indebære, at tilstedeværelsen af komplekse multidimensionale strukturer, der kræver skøn, der tager denne kompleksitet i betragtning (fx, Tarkkonen og Vehkalahti, 2005; Grøn og Yang, 2015)., Det er vigtigt at udrydde den fejlagtige tro på, at α-koefficienten er en god indikator for unidimensionalitet, fordi dens værdi ville være højere, hvis skalaen var unidimensional. Faktisk er det nøjagtige modsatte tilfældet, som det blev vist af Sijtsma (2009), og dets anvendelse under sådanne forhold kan føre til, at pålideligheden er stærkt overvurderet (Raykov, 2001). Før beregning af α er det derfor nødvendigt at kontrollere, at dataene passer til unidimensionelle modeller.
antagelsen om tau-ækvivalens (dvs .,, den samme sande score for alle testelementer eller lige faktorbelastninger af alle elementer i en faktormodel) er et krav om, at α svarer til pålidelighedskoefficienten (Cronbach, 1951). Hvis antagelsen om Tau-ækvivalens overtrædes, vil den sande pålidelighedsværdi blive undervurderet (Raykov, 1997; Graham, 2006) med et beløb, der kan variere mellem 0,6 og 11,1% afhængigt af overtrædelsens grovhed (Green og Yang, 2009a). At arbejde med data, der overholder denne antagelse, er generelt ikke levedygtig i praksis (Teo og Fan, 2013); den congeneriske model (dvs .,, forskellige faktor belastninger) er mere realistisk.
kravet om multivariant normalitet er mindre kendt, og som påvirker både puntual pålidelighed skøn og muligheden for at etablere konfidensintervaller (Dunn et al., 2014). Sheng og Sheng (2012), som er observeret for nylig, at når fordelingerne er skæve og/eller leptokurtic, en negativ bias er produceret, når koefficienten α beregnes; lignende resultater blev præsenteret af Grønne og Yang (2009b) i en analyse af konsekvenserne af den ikke-normale fordelinger i forbindelse med vurdering af pålidelighed., Undersøgelse af skævhedsproblemer er vigtigere, når vi ser, at forskere i praksis sædvanligvis arbejder med skæve skalaer (Micceri, 1989; Norton et al., 2013; Ho og Yu, 2014). F. eks Micceri (1989) anslået, at omkring 2/3 af evne og over 4/5 af psykometriske foranstaltninger udviste mindst moderat asymmetri (dvs.skævhed omkring 1). På trods af dette er virkningen af skævhed på pålidelighedsestimering blevet lidt undersøgt.,
i Betragtning af den overvældende litteratur om de begrænsninger og bias α koefficient (Revelle og Zinbarg, 2009; Sijtsma, 2009, 2012; Cho og Kim, 2015; Sijtsma og van Ark, 2015), opstår spørgsmålet om, hvorfor forskere fortsætte med at bruge α, når der findes alternative koefficienter, der kan overvinde disse begrænsninger. Det er muligt, at overskuddet af procedurer til estimering af pålidelighed udviklet i det sidste århundrede har oscieret debatten. Dette ville have været yderligere forværret af enkelheden ved beregning af denne koefficient og dens tilgængelighed i kommercielle soft .are.,
vanskeligheden ved at estimere p..’pålidelighedskoefficient ligger i dens definition p..’ ==t2∕σ22, som inkluderer den sande score i varianstælleren, når dette af natur ikke kan observeres. Α-koefficienten forsøger at tilnærme denne uobserverbare varians fra kovariansen mellem elementerne eller komponenterne. Cronbach (1951) viste, at der i mangel af tau-ækvivalens, α koefficient (eller Guttman”s lambda 3, hvilket svarer til α) var en god nedre grænse tilnærmelse., Således, når de antagelser, der er overtrådt problem udmønter sig i at finde de bedst mulige nedre grænse; ja, dette navn er givet til den Største Nedre grænse metode (GLB), som er den bedst mulige tilnærmelse fra en teoretisk vinkel (Jackson og Agunwamba, 1977; Woodhouse og Jackson, 1977; Shapiro og ti Berge, 2000; Sočan, 2000; ti Berge og Sočan, 2004; Sijtsma, 2009). Revelle og .inbarg (2009) mener dog, at ω giver en bedre nedre grænse end GLB., Der er derfor en uafklaret debat om, hvilken af disse to metoder, der giver den bedste nedre grænse; desuden er spørgsmålet om ikke-normalitet ikke blevet udtømmende undersøgt, som det nuværende arbejde diskuterer.
ω Koefficienter
McDonald ‘ (1999) foreslået wt koefficient til vurdering af pålidelighed fra en faktoriel analyse ramme, som kan udtrykkes formelt som:
Hvor λj er indlæsning af punkt j, λj2 er et fællesskab af item j og ψ svarer til det unikke., Wt koefficient, ved at inkludere de lambdas i formler, er velegnet både når tau-ækvivalens (dvs, lig faktor loadings af alle test poster) eksisterer (wt falder sammen matematisk, α), og når elementer med forskellige forskelsbehandling, som er til stede i repræsentationen af konstruere (dvs, anden faktor loadings for items: congeneric målinger). Følgelig korrigerertt undervurderingsforspændingen af α, når antagelsen om tau-ækvivalens overtrædes (Dunn et al ., 2014) og forskellige undersøgelser viser, at det er et af de bedste alternativer til estimering af pålidelighed (.inbarg et al.,, 2005, 2006; Revelle og Revelinbarg, 2009), selvom den hidtil fungerer under skævhedsbetingelser, er ukendt.
Når du er sammenhæng mellem fejl, eller der er mere end én latente dimensioner i data, bidrag for hver dimension til den samlede varians forklaret er anslået, at få de såkaldte hierarkiske ω (wh), som gør det muligt for os at rette de værste overvurdering bias af α med flerdimensionelle data (se Tarkkonen og Vehkalahti, 2005; Zinbarg et al., 2005; Revelle og andinbarg, 2009)., Koefficienter WHH og .t er ækvivalente i unidimensionelle data, så vi vil henvise til denne koefficient simpelthen som ω.
Største Nedre grænse (GLB)
Sijtsma (2009) viser i en række undersøgelser, at en af de mest magtfulde estimatorer for pålidelighed er GLB—udledes af Woodhouse og Jackson (1977) fra de antagelser, der af Klassisk Test Teori (Cx = Ct + Ce)—en inter-item kovarians matricen for de observerede item scores Cx. Det opdeles i to dele: summen af Inter-item covariance Matri.for item true scores Ct; og Inter-item error covariance Matri. Ce (ten Berge og Soanan, 2004)., Dens udtryk er:
hvor test .2 er testvariansen, og tr(Ce) henviser til sporet af Inter-item error covariance Matri., som det har vist sig så vanskeligt at estimere. En løsning har været at anvende faktorielle procedurer såsom Minimum Rank Factor Analysis (en procedure kendt som glb.fa). For nylig GLB algebraisk (GLBa) procedure er blevet udviklet ud fra en algoritme udtænkt af Andreas Moltner (Moltner og Revelle, 2015)., Ifølge Revelle (2015a) denne procedure vedtager den form, der er mest trofaste til den oprindelige definition af Jackson og Agunwamba (1977), og det har den ekstra fordel af at indføre en vektor til at tabe den elementer af betydning (Al-Homidan, 2008).
På trods af sine teoretiske styrker har GLB været meget lidt brugt, selv om nogle nylige empiriske undersøgelser har vist, at denne koefficient giver bedre resultater end α (Lila et al., 2014) og α og 2014 (2014ilco and Et Al ., 2014)., Ikke desto mindre har det i små prøver under antagelse af normalitet en tendens til at overvurdere den sande pålidelighedsværdi (Shapiro og ten Berge, 2000); imidlertid forbliver dens funktion under ikke-normale forhold ukendt, specifikt når distributionerne af emnerne er asymmetriske.
i betragtning af de koefficienter, der er defineret ovenfor, og forspændingerne og begrænsningerne for hver, er formålet med dette arbejde at evaluere robustheden af disse koefficienter i nærvær af asymmetriske elementer, idet man også overvejer antagelsen om tau-ækvivalens og stikprøvestørrelsen.,
Metoder
fremskaffelse af Data
De data, der blev genereret ved brug af R (R Development Core Team, 2013) og RStudio (Racine, 2012) – software, efter fakultet-model:
hvor Xij er den simulerede svar på emne, jeg i punkt j, λjk er indlæsning af punkt j i Faktor k (som blev genereret af unifactorial model); Fk er den latente faktor, der genereres af en standardiseret normalfordeling (middelværdi 0 og varians 1), og ej er den tilfældige målefejl for hvert element, også efter en standardiseret normalfordeling.,
Skæve elementer: Standard normal Xij blev omdannet til at generere ikke-normale fordelinger ved hjælp af den procedure, der er foreslået af Headrick (2002) anvendelse af femte orden polynomium forvandler:
Simulerede Forhold
for At vurdere effektiviteten af pålidelighed koefficienter (α, ω, GLB, og GLBa) vi arbejdede med tre stikprøvestørrelser (250, 500, 1000), to test-størrelser: kort (6 emner) og lang (12 items), to betingelser for tau-ækvivalens (den ene med tau-ækvivalens og én uden, dvs,, congeneric) og den gradvise inkorporering af asymmetriske elementer (fra alle elementer er normale til alle elementer er asymmetriske). I den korte teste pålideligheden blev sat på 0.731, som i overværelse af tau-ækvivalens opnås med seks elementer, der med faktor loadings = 0.558; mens congeneric model er opnået ved at sætte faktor loadings på værdier af 0.3, 0.4, 0.5, 0.6, 0.7, og 0,8 (se Tillæg i). I den lange test af 12 varer blev pålideligheden sat til 0.,845 tager de samme værdier som i den korte test for både tau-ækvivalens og congeneric model (i dette tilfælde var der to elementer for hver værdi af lambda). På denne måde blev 120 betingelser simuleret med 1000 replikaer i hvert tilfælde.
Analyse af Data
De vigtigste analyser blev udført ved hjælp af Psych (Revelle, 2015b) og GPArotation (Bernaards og Jennrich, 2015) pakker, som giver α-og ω blive estimeret. Der blev anvendt to edb-metoder til estimering af GLB: glb.fa (Revelle, 2015a) og glb.,algebraisk (Moltner and Revelle, 2015), sidstnævnte arbejdede af forfattere som Hunt og Bentler (2015).
for at vurdere nøjagtigheden af de forskellige estimatorer med at inddrive pålidelighed, har vi beregnet Root Mean Square Error (RMSE) og bias. Den første er gennemsnittet af forskellene mellem den estimerede og den simulerede pålidelighed og formaliseres som:
hvor ^ ^ er den estimerede pålidelighed for hver koefficient, the den simulerede pålidelighed og Nr antallet af replikaer., Den % bias forstås som forskellen mellem gennemsnittet af de forventede pålidelighed og simuleret pålidelighed og er defineret som:
I begge indeks, jo større værdi, jo større unøjagtighed af estimatoren, men i modsætning til RMSE, bias kan være positiv eller negativ; i dette tilfælde yderligere oplysninger, der ville være opnået, om koefficienten er undervurderer eller overvurderer de simulerede pålidelighed parameter., Efter anbefaling af Hoogland og Boomsma (1998) værdier af RMSE < 0,05 og % bias < 5% blev anset for acceptabel.
resultater
de vigtigste resultater kan ses i tabel 1 (6 poster) og tabel 2 (12 poster). Disse viser RMSE og % bias af koefficienterne i tau-ækvivalens og congeneric betingelser, og hvordan skævheden af testfordelingen stiger med den gradvise inkorporering af asymmetriske elementer.
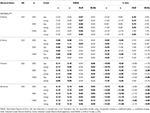
Tabel 1., RMSE og Bias med tau-ækvivalens og congeneric betingelse for 6 poster, tre stikprøvestørrelser og antallet af skæve elementer.
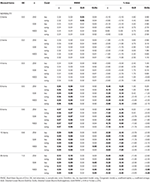
Tabel 2. RMSE og Bias med tau-ækvivalens og congeneric betingelse for 12 poster, tre stikprøvestørrelser og antallet af skæv poster.
kun under betingelser med tau-ækvivalens og normalitet (skævhed < 0.2) observeres det, at α-koefficienten estimerer den simulerede pålidelighed korrekt, som ω., I den congeneriske tilstand korrigerer correc undervurderingen af.. Både GLB og GLBa udviser en positiv bias under normalitet, men GLBa viser ca. ½ mindre % bias end GLB (se tabel 1). Hvis vi overvejer prøvestørrelse, observerer vi, at når teststørrelsen stiger, mindskes den positive bias af GLB og GLBa, men forsvinder aldrig.
I asymmetriske forhold, vi ser i Tabel 1, at både α-og ω udgør en uacceptabel præstation med stigende RMSE og underestimations, som kan nå op bias > 13% af α-koefficienten (mellem 1 og 2% lavere for ω)., GLB-og GLBa-koefficienterne giver en lavere RMSE, når testskyggen eller antallet af asymmetriske elementer stiger (se tabel 1, 2). GLB-koefficienten præsenterer bedre estimater, når testskydningsværdien af testen er omkring 0.30; GLBa er meget ens og præsenterer bedre estimater end ω med en testskydningsværdi omkring 0.20 eller 0.30. Men når skævhedsværdien stiger til 0, 50 eller 0, 60, præsenterer GLB bedre ydelse end GLBa. Teststørrelsen (6 eller 12emstems) har en langt vigtigere effekt end prøvestørrelsen på estimaternes nøjagtighed.,
Diskussion
I denne undersøgelse, at fire faktorer, der blev manipuleret: tau-ækvivalens eller congeneric model, prøve størrelse (250, 500 og 1000), antallet af teststoffer (6 og 12), og antallet af asymmetriske elementer (fra 0 asymmetriske elementer til alle de emner, der asymmetriske) med henblik på at vurdere robustheden af tilstedeværelsen af asymmetrisk data i de fire pålidelighed koefficienter, der er analyseret. Disse resultater diskuteres nedenfor.,
under betingelser med tau-ækvivalens konvergerer α-og coefficients-koefficienterne, men i mangel af tau-ækvivalens (congeneric) præsenterer ω altid bedre estimater og mindre RMSE og % bias end α. I denne mere realistisk betingelse derfor (Grøn og Yang, 2009a; Yang og Grøn, 2011), α bliver et negativt forudindtaget pålidelighed estimator (Graham, 2006; Sijtsma, 2009; Cho og Kim, 2015) og ω er altid at foretrække, at α (Dunn et al., 2014). I tilfælde af ikke-overtrædelse af antagelsen om normalitet er ω den bedste estimator for alle de evaluerede koefficienter (Revelle og andinbarg, 2009).,
Med hensyn til prøvestørrelse observerer vi, at denne faktor har en lille effekt under normalitet eller en lille afvigelse fra normalitet: RMSE og bias mindskes, når prøvestørrelsen stiger. Ikke desto mindre kan det siges, at for disse to koefficienter, med stikprøvestørrelse på 250 og normalitet, opnår vi relativt nøjagtige estimater (Tang og Cui, 2012; Javali et al., 2011)., For GLB og GLBa koefficienter, som stikprøve øger RMSE og bias har en tendens til at aftage; men de opretholder en positiv bias for den tilstand af normalitet selv med store stikprøvestørrelser af 1000 (Shapiro og ti Berge, 2000; ti Berge og Sočan, 2004; Sijtsma, 2009).
for teststørrelsen observerer vi generelt en højere RMSE og bias med 6 elementer end med 12, hvilket antyder, at jo højere antallet af elementer er, jo lavere er RMSE og bias for estimatorerne (Cortina, 1993). Generelt opretholdes tendensen for både 6 og 12 poster.,
Når vi ser på effekten af gradvis integrering af asymmetriske elementer i datasættet, vi observerer, at α-koefficienten er meget følsomme over for asymmetriske elementer; disse resultater ligner dem, der findes ved Sheng og Sheng (2012) og Grøn og Yang (2009b). Koefficient presents præsenterer lignende RMSE og bias værdier til dem af α, men lidt bedre, selv med tau-ækvivalens. GLB og GLBa viser sig at præsentere bedre estimater, når testskygheden afviger fra værdier tæt på 0.
i betragtning af at det i praksis er almindeligt at finde asymmetriske data (Micceri, 1989; Norton et al.,, 2013; Ho og Yu, 2014), sijtsma ” s forslag (2009) om at bruge GLB som en pålidelighed estimator synes velbegrundet. Andre forfattere, såsom Revelle og .inbarg (2009) og Green and Yang (2009a), anbefaler brugen af ω, men denne koefficient gav kun gode resultater i normalitetens tilstand eller med lav andel skævhed. Under alle omstændigheder gav disse koefficienter større teoretiske og empiriske fordele end α. Ikke desto mindre anbefaler vi forskere at studere ikke kun punktlige skøn, men også at gøre brug af interval estimering (Dunn et al., 2014).,
disse resultater er begrænset til de simulerede forhold, og det antages, at der ikke er nogen sammenhæng mellem fejl. Dette ville gøre det nødvendigt at foretage yderligere undersøgelser for at evaluere, hvordan de forskellige pålidelighed koefficienter med mere komplekse multidimensionale strukturer (Reise, 2012; Grøn og Yang, 2015), og i overværelse af ordenstal og/eller kategoriske data, som ikke-overensstemmelse med antagelsen om normalitet er normen.
konklusion
når de samlede testresultater normalt fordeles (dvs ., er alle elementer normalt fordelt) should bør være det første valg efterfulgt af followed, da de undgår overvurdering problemer præsenteret af GLB. Men når der er en lav eller moderat test skævhed GLBa bør anvendes. GLB anbefales, når andelen af asymmetriske genstande er høj, da det under disse forhold ikke er tilrådeligt at anvende både α Og ω som pålidelighedsestimatorer, uanset prøvestørrelsen.
Forfatterbidrag
udvikling af ideen om forskning og teoretisk ramme (it, JA). Konstruktion af den metodologiske ramme(IT, JA)., Udvikling af R-sprogsynta .en (it, JA). Dataanalyse og fortolkning af data (IT, JA). Diskussion af resultaterne i lyset af nuværende teoretiske baggrund (JA, IT). Forberedelse og skrivning af artiklen (JA, det). Generelt har begge forfattere bidraget lige til udviklingen af dette arbejde.,
Finansiering
Den første forfatter, som offentliggøres modtagelsen af følgende finansiel støtte til forskning, forfatterskab, og/eller offentliggørelse af denne artikel: DET har modtaget økonomisk støtte fra den Chilenske Nationale Kommissionen for Videnskabelig og Teknologisk Forskning (CONICYT) “Becas Chile” Ph.d. – Stipendium program (Bevilling nr: 72140548).
Erklæring om interessekonflikt
forfatterne erklærer, at forskningen blev udført i mangel af kommercielle eller økonomiske forhold, der kunne fortolkes som en potentiel interessekonflikt.
Cronbach, L. (1951)., Koefficient alfa og prøvningernes interne struktur. Psychometrika 16, 297-334. doi: 10.1007/BF02310555
CrossRef Fuld Tekst | Google Scholar
McDonald, R. (1999). Testteori: en samlet behandling. Mahwah, NJ: Lawrence Erlbaum Associates.
Google Scholar
R Development Core Team (2013). R: et sprog og miljø for statistisk databehandling. Foundationien: R Foundation for Statistical Computing.
Raykov, T. (1997)., Scale reliability, cronbach”s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package “psych.,”Tilgængelig online på: http://org/r/psych-manual.pdf
Shapiro, A., and ten Berge, J. M. F. (2000). Den asymptotiske bias af mindste sporfaktoranalyse, med anvendelser til den største nedre grænse for pålidelighed. Psychometrika 65, 413-425. doi: 10.1007/BF02296154
CrossRef Fuld Tekst | Google Scholar
ti Berge, J. M. F., og Sočan, G. (2004). Den største nedre grænse for pålideligheden af en test og hypotesen om unidimensionalitet. Psychometrika 69, 613-625. doi: 10.,1007/BF02289858
CrossRef Fuld Tekst | Google Scholar
Woodhouse, B., og Jackson, P. H. (1977). Nedre grænser for pålideligheden af den samlede score på en test, der består af ikke-homogene elementer: II: en søgning til at finde den største nedre grænse. Psychometrika 42, 579-591. doi: 10.1007 | bf02295980
CrossRef fuldtekst/Google Scholar
Appendiks i
r syntaks til estimering af pålidelighedskoefficienter fra Pearson”s korrelationsmatricer., Sammenhængen værdier uden for diagonalen er beregnet ved at gange faktor ilægning af elementer: (1) tau-tilsvarende model, de er alle lige til at 0.3114 (λiλj = 0.558 × 0.558 = 0.3114) og (2) congeneric model de varierer som en funktion af de forskellige faktor loading (fx, matrix-element, a1, 2 = λ1λ2 = 0.3 × 0.4 = 0.12). I begge eksempler er den sande pålidelighed 0.731.
> omega(Cr,1)$alpha # standardiseret Cronbach”s α
0.731
> omega(Cr,1)$omega.tot # koefficient total total
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach”s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731