Pythagoras” Sætning

Pythagoras

for mere End 2000 år siden var der en forbløffende opdagelse, om trekanter:

Når en trekant har en ret vinkel (90°) …

… og firkanter er lavet på hver aftre sider,…

… så den største firkant har nøjagtig samme område som de to andre firkanter sat sammen!,

Det kaldes “Pythagoras” Sætning”, og kan være skrevet i en kort formel:

a2 + b2 = c2

Bemærk:

• c er den længste side af trekanten
• a og b er de to andre sider

Definition

Den længste side af trekanten, kaldes “hypotenusen”, så den formelle definition er:

sikker … ?

Lad”s se om det virkelig virker ved hjælp af et eksempel.

Hvorfor er dette nyttigt?

Hvis vi kender længderne på to sider af en retvinklet trekant, kan vi finde længden på den tredje side. (Men husk det virker kun på retvinklede trekanter!)

Hvordan bruger jeg det?,

Skriv det ned, som en ligning:

Så vi bruger algebra at finde eventuelle manglende værdi, som i disse eksempler:

Du kan også læse om Kvadrater og kvadratrødder at finde ud af, hvorfor √169 = 13

Det virker også den anden vej rundt, for: når de tre sider i en trekant gøre a2 + b2 = c2, så trekanten er retvinklet.,

og du kan selv bevise sætningen !

Hent papirpen og saks, og brug derefter følgende animation som vejledning:

• Tegn en retvinklet trekant på papiret, hvilket giver masser af plads.,
• Tegn en firkant langs hypotenusen (den længste side)
• Trække i samme størrelse-pladsen på den anden side af hypotenusen
• Tegne linjer, som vist på den animation, som denne:
• 
• Skære figurerne
• Arrangere dem, så du kan bevise, at den store plads, er det samme område som de to firkanter på andre sider

en Anden, Utrolig Enkel, Bevis

Her er en af de ældste beviser på, at pladsen på den lange side har det samme område som de andre pladser.,

se animationen, og vær opmærksom, når trekanterne begynder at glide rundt.

du ønsker måske at se animationen et par gange for at forstå, hvad der sker.

den lilla trekant er den vigtige.

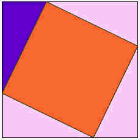bliver til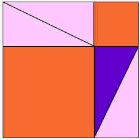