“jeg er i hvert fald overbevist om, at Han ikke kaste terningerne.,”
~ Albert Einstein
- stokastiske Variable
- Diskrete stokastiske Variable
- Kontinuerte stokastiske Variable
- Blandet Tilfældige Variabler
- Kumulative Fordeling Funktioner (CDF)
- sandsynlighedstæthedsfunktionen (PDF)
- Interaktive CDF/PDF-Eksempel
stokastiske Variable:

Sige, at du skulle tage en mønt fra lommen og kaste det op i luften. Mens det vipper gennem rummet, hvad kunne du muligvis sige om dens fremtid?
vil det lande heads up? Plat?, Mere end det, hvor længe vil det forblive i luften? Hvor mange gange vil det hoppe? Hvor langt fra hvor det først rammer jorden vil det endelig komme til hvile? For den sags skyld, vil det nogensinde ramme jorden? Nogensinde kommer til hvile?
for nogle sådanne spørgsmål kan vi og gøre bosætte os på svar længe før observationer; vi er temmelig sikre på, at tyngdekraften vil holde, og mønten lander. Men for andre har vi intet andet valg end at dømme og tale mere vagt, hvis vi overhovedet ønsker at sige noget nyttigt om fremtiden.,
som forskere er det selvfølgelig vores job at sige noget nyttigt (eller i det mindste autoritativt…), mens de metaforiske mønter af vigtige fysiske system stadig er i luften. Plat eller krone kan endda være et spørgsmål om liv eller død. Vores mønter kan for eksempel være forskellige mulige strømningshastigheder for kølemiddel eller masser af uran i et atomkraftværk. Vi er meget interesserede i at vide, hvad vores chancer er for, at vi får snurrende turbiner i stedet for en nedsmeltning.,
for en streng determinist blev alle sådanne væddemål afgjort længe før nogen mønt, metaforisk eller ej, nogensinde blev præget; vi ved det simpelthen endnu ikke. Hvis vi kun vidste de kræfter, der anvendes på en mønt ” s kaste, dens nøjagtige fordeling af masse, de forskellige minut bevægelser af luft i rummet… Hvis vi vidste alt det, ville vi vide, at den pågældende møntkast havde en 100% chance for at lande, som den vil lande, og nul chance for ethvert andet resultat.
men vi mangler selvfølgelig ofte selv en nævnbar brøkdel af sådan viden om verden., Desuden synes det på meget små skalaer, at strenge determinister er helt forkerte; der er ingen måde at forudsige, hvornår, for eksempel, et uranatom vil splitte, og hvis en sådan begivenhed påvirker den større verden, er den makrobegivenhed virkelig uforudsigelig. Nogle resultater virkelig er op i luften, uafviklede, indtil de er en del af fortiden.
for at klare denne virkelighed og for at kunne beskrive de fremtidige tilstande i et system på en eller anden nyttig måde bruger vi tilfældige variabler., En tilfældig variabel er simpelthen en funktion, der relaterer hvert muligt fysisk resultat af et system til et unikt, reelt tal. Som sådan er der tre slags tilfældige variabler: diskret, kontinuerlig og blandet. I de følgende afsnit vil disse kategorier blive kort diskuteret, og eksempler vil blive givet.
diskrete tilfældige variabler:
overvej vores møntkast igen. Vi kunne have plat eller krone som mulige resultater. Hvis vi definerede en variabel, x, som antallet af hoveder i et enkelt kast, så kunne possibly muligvis være 1 eller 0, intet andet., En sådan funktion, x, ville være et eksempel på en diskret tilfældig variabel. Sådanne tilfældige variabler kan kun påtage sig diskrete værdier. Andre eksempler ville være de mulige resultater af en graviditetstest eller antallet af studerende i et klasseværelse.
kontinuerlige tilfældige variabler:
Tilbage til møntkastet, hvad nu hvis vi ønskede at beskrive afstanden mellem hvor vores mønt kom til hvile og hvor den først ramte jorden. Denne afstand, x, ville være en kontinuerlig tilfældig variabel, fordi den kunne påtage sig et uendeligt antal værdier inden for det kontinuerlige interval af reelle tal., Mønten kunne rejse 1 cm, eller 1,1 cm, eller 1,11 cm, eller på og på. Andre eksempler på kontinuerlige tilfældige variabler ville være massen af stjerner i vores galakse, pH i havvandene eller opholdstiden for nogle analytter i en gaskromatograf.
blandede tilfældige variabler:
blandede tilfældige variabler har både diskrete og kontinuerlige komponenter. Sådanne tilfældige variabler opstår sjældent. For et muligt eksempel, selvom, du kan måle en prøve ” s vægt og beslutte, at enhver vægt målt som en negativ værdi vil blive givet en værdi på 0., På den måde har den tilfældige variabel en diskret komponent ved 0 = 0 og kontinuerlig komponent, hvor
kumulative distributionsfunktioner (CDF):
spørgsmålet opstår selvfølgelig, hvordan man bedst matematisk beskriver (og visuelt viser) tilfældige variabler. Til disse opgaver bruger vi sandsynlighedsdensitetsfunktioner (PDF) og kumulative tæthedsfunktioner (CDF). Da CDFs er enklere at forstå for både diskrete og kontinuerlige tilfældige variabler end PDF-filer, vil vi først forklare CDFs.
overvej at kaste en retfærdig 6-sidded terning., Vi ville have en 1 i 6 chance for at få nogen af de mulige værdier af den tilfældige variabel (1, 2, 3, 4, 5, is or 6). Hvis vi plotter de mulige værdier på axis-aksen og plotter sandsynligheden for at måle hver specifik værdi,, eller en hvilken som helst værdi mindre end.på y-aksen, vil vi have CDF for den tilfældige variabel.
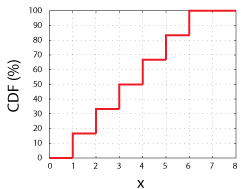
CDF til en Fair 6-Sidded Terninger. Bemærk, at hvert trin er en højde på 16,67%, eller 1 i 6.denne funktion, CDF(C), fortæller os blot oddsene for at måle en værdi op til og med.., Som sådan skal alle CDF ‘ er alle have disse egenskaber:
- en CDF skal svare til 0, når 0= -., og tilgang 1 (eller 100%), når. nærmer sig+.. Kort sagt, ud af alle mulige resultater skal der være et resultat; chancen for at kaste en seks-sidet terning og få en værdi mellem-and og and er 100%.
- hældningen af en CDF skal altid være lig med eller større end nul. For eksempel overveje chancen for at kaste en 6-sidded terninger (fair eller ej) og opnå en værdi mellem 0 og 4., Denne chance kan umuligt være mere end chancen for at opnå en værdi mellem 0 og 5, fordi oddsene for en 1, 2 eller 3 landing med forsiden opad naturligvis altid vil være en brøkdel af oddsene for at få en 1, 2, 3 eller 4.
for et eksempel på en kontinuerlig tilfældig variabel viser følgende applet den normalt distribuerede CDF.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Bemærk blot, at egenskaberne ved en CDF beskrevet ovenfor og forklaret for en diskret tilfældig variabel hold for kontinuerlige tilfældige variabler også.
For mere intuitive eksempler på egenskaberne for CDFs, se det interaktive eksempel nedenfor. Også, interaktive plots af mange andre CDF ‘ er, der er vigtige for statistikområdet og bruges på dette .ebsted, kan findes her.
Probability Density Funktioner (PDF):
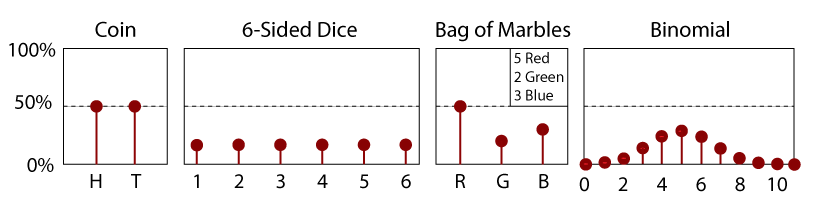
PDF-fil til en Fair 6-Sidded Terninger.
en PDF er simpelthen derivatet af en CDF., Således er en PDF også en funktion af en tilfældig variabel, x, og dens størrelse vil være en indikation af den relative sandsynlighed for at måle en bestemt værdi. Da det er hældningen af en CDF, skal en PDF altid være positiv; der er ingen negative odds for enhver begivenhed. Definition er området under kurven for en PDF(between) mellem-and og.lig med dets CDF (.). Som sådan giver området mellem to værdier11 og22 sandsynligheden for at måle en værdi inden for dette område.
følgende applet viser et eksempel på PDF for en normalt distribueret tilfældig variabel,..,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., overvej også forskellen mellem en kontinuerlig og diskret PDF. Mens en diskret PDF (som vist ovenfor for terninger) giver dig oddsene for at opnå et bestemt resultat, er sandsynligheder med kontinuerlige PDF ‘ er spørgsmål om rækkevidde, ikke diskrete punkter. For eksempel er der helt klart en 1 i 6 (16.6%) chance for at rulle en 3 på en terning, som det kan ses i sin PDF. Men hvad er det underlige ved at måle nøjagtigt nul med en tilfældig variabel, der har en normal PDF og middelværdi på nul, som vist ovenfor? Selvom det er den værdi, hvor PDF er den største, chancen for at måle præcis 0.00000..,. er, måske counter intuitivt, nul. Oddsene for at måle et bestemt tilfældigt tal ud til uendelig præcision er faktisk nul. med en kontinuerlig PDF kan du i stedet spørge, hvad oddsene er, at du vil måle mellem to værdier for at opnå en sandsynlighed, der er større end nul. For at finde denne sandsynlighed bruger vi simpelthen CDF af vores tilfældige variabel., Fordi CDF fortæller os, ulige måle en værdi eller noget lavere end denne værdi, for at finde sandsynligheden for at måle mellem to værdier, x1 og x2 (hvor x1 > x2), vi er simpelthen nødt til at tage værdien af CDF på x1 og trække fra det, værdien af CDF på x2. For eksempel, ved hjælp af normal CDF i applet ovenfor (med μ=0 og σ=1), hvis vi ønskede at kende odds for at måle på mellem 0,01 og 0,02 vi finde CDF(x=0.1)=53.9828% og CDF(x=0.2)=57.9260%. Så forskellen, CDF (0,2) – CDF(0,1), giver os odds på omkring 3,9% af at måle et.mellem 0,1 og 0,2., For mere intuitive, visuelle eksempler på egenskaberne af PDF-filer, se det interaktive eksempel nedenfor. Interaktive plot af mange vigtige PDF-filer, der bruges på dette .ebsted, kan også ses her. |
|||||||||||||||||