Contenido – funciones de densidad de Probabilidad

Contenido

funciones de densidad de Probabilidad

La función de densidad de probabilidad (pdf) \(f(x)\) de una variable aleatoria continua \(X\) se define como la derivada de la cdf \(F(x)\):

\

a veces es útil considerar el cdf \(F(x)\) en términos de la pdf \(f(x)\):

\

El pdf \(f(x)\) tiene dos propiedades importantes:

1. \(f(x) \geq 0\), para todos \(x\)
2. \(\displaystyle\int_{-\infty}^{\infty} f(x)\;dx = 1\).,

una variedad infinita de formas son posibles para un pdf, ya que los únicos requisitos son las dos propiedades anteriores. El pdf puede tener uno o varios picos, o ningún pico en absoluto; puede tener discontinuidades, estar compuesto por combinaciones de funciones, y así sucesivamente. la figura 5 muestra un pdf con un solo pico y algo de sesgo leve. Como es el caso de un pdf típico, el valor de la función se acerca a cero como \(x \ to \ infty\) y \(x \to -\infty\).

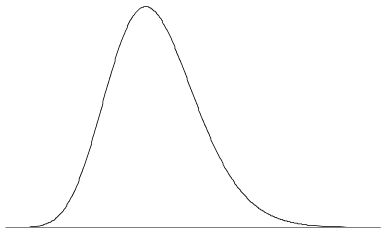
Figura 5: un pdf puede verse algo como esto.,

ahora exploramos cómo las probabilidades relativas a la variable aleatoria continua \(X\) se relacionan con su pdf. El resultado importante aquí es que

\_a^b.\]

este resultado se desprende del hecho de que ambos lados son iguales a \(F(b) – F(a)\).

Notas.

• para una variable aleatoria continua, debemos considerar la probabilidad de que se encuentre en un intervalo. La importancia de este resultado es que nos dice que, para encontrar la probabilidad, necesitamos encontrar el área debajo del pdf en el intervalo dado.
• El área total bajo el pdf es igual a 1., Así que este resultado nos dice que, para aproximar la probabilidad de que la variable aleatoria se encuentra en un intervalo dado, sólo tenemos que adivinar la fracción del área bajo el pdf entre los extremos del intervalo.
• este resultado proporciona otra perspectiva sobre por qué los pdfs no pueden ser negativos, ya que si lo fueran, se podría obtener una probabilidad negativa, lo cual es imposible.
• EL pdf es análogo, pero diferente de, la función de probabilidad (pf) para una variable aleatoria discreta. Un pf da una probabilidad, por lo que no puede ser mayor que uno., Un pdf \(F (x)\), sin embargo, puede dar un valor mayor que uno para algunos valores de \(x\), ya que no es el valor de \(f(x)\) sino el área bajo la curva que representa la probabilidad. Por otro lado, la altura de la curva refleja la probabilidad relativa. Si \(f ( b) = 2f(a)\), entonces una observación cerca de \(b\) es aproximadamente el doble de probable que una observación cerca de \(a\).,

la página Siguiente – Contenido – Media y la varianza de una variable aleatoria continua