un modelo de regresión para datos de supervivencia
anteriormente escribí sobre cómo calcular la curva de Kaplan–Meier para datos de supervivencia. Como estimador no paramétrico, hace un buen trabajo al dar una mirada rápida a la curva de supervivencia para un conjunto de datos. Sin embargo, lo que no le permite hacer es modelar el impacto de las covariables en la supervivencia. En este artículo, nos centraremos en el modelo de riesgos proporcionales de Cox, uno de los modelos más utilizados para los datos de supervivencia.
profundizaremos en cómo calcular las estimaciones., Esto es valioso porque veremos que las estimaciones dependen solo del orden de los fallos y no de sus tiempos reales. También discutiremos brevemente algunos temas difíciles sobre la inferencia causal que son especiales para el análisis de supervivencia.
normalmente pensamos en los datos de supervivencia en términos de curvas de supervivencia como la siguiente.,
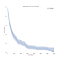
En el eje x tenemos el tiempo en días. En el eje y, tenemos (un estimador para) el porcentaje (técnicamente, proporción) de sujetos en la población que «sobreviven» a ese tiempo. Sobrevivir puede ser figurativo o literal., Podría ser si las personas viven hasta cierta edad, si una máquina hace que sea una cierta cantidad de tiempo sin descomponerse, o podría ser si alguien permanece desempleado una cierta cantidad de tiempo después de perder su trabajo.
fundamentalmente, la complicación en el análisis de supervivencia es que algunos sujetos no tienen su» muerte » observada. Es posible que todavía estén vivos, que una máquina todavía esté funcionando o que alguien todavía esté desempleado en el momento en que se recopilan los datos., Tales observaciones se denominan «censuradas por la derecha» y lidiar con la censura significa que el análisis de supervivencia requiere diferentes herramientas estadísticas.
denotamos la función survivor como S, una función del tiempo. Su salida es el porcentaje de sujetos que sobreviven en el tiempo t. (de nuevo, es técnicamente una proporción entre 0 y 1, pero usaré las dos palabras indistintamente). Por simplicidad haremos la suposición técnica de que si esperamos lo suficiente todos los sujetos «morirán».»
indexaremos los sujetos con un subíndice como i O j., El fracaso de los tiempos de la totalidad de la población será indicado con un similar subíndice de la variable de tiempo t.

Otra sutileza a considerar es si estamos tratando a tiempo como discretos (de la semana, por semana, por ejemplo) o continua. Filosóficamente hablando, solo medimos el tiempo en incrementos discretos (al segundo más cercano, por ejemplo)., Comúnmente, nuestros datos solo nos dirán si alguien murió en un año determinado o si una máquina falló en un día determinado. Voy a ir y venir entre los casos discretos y continuos en el interés de mantener la exposición tan clara como sea posible.
Cuando estamos tratando de modelar los efectos de las covariables (por ejemplo, edad, género, raza, fabricante de la máquina), normalmente estaremos interesados en comprender el efecto de la covariable en la tasa de riesgo. La tasa de riesgo es la probabilidad instantánea de fracaso/muerte/transición de estado en un tiempo T dado, condicionada a que ya haya sobrevivido ese tiempo., Vamos a denotarlo λ (t). El tratamiento del tiempo como discretos:
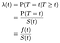
Donde f es el total de densidad de probabilidad de fracasar en el tiempo t. Podemos unificar el discretos y continuos casos permitiendo funciones delta en la densidad de probabilidad de la «función». Así, el resultado λ = f / S es el mismo para el caso continuo.
Vamos a arreglar un ejemplo., Consideremos el contexto de un ensayo clínico en el que un medicamento inicialmente hace que una enfermedad entre en remisión. Diremos que el medicamento «falla» para un sujeto cuando la enfermedad comienza a progresar para un sujeto. Finalmente, supongamos que el estado de la enfermedad de los sujetos se mide cada semana. Entonces si λ (3) = 0.1, eso significa que hay un 10% de probabilidad de que, para un sujeto dado, si todavía están en remisión antes de la semana 3, su enfermedad comenzará a progresar en la semana 3. El otro 90% permanecerá en remisión.,
a continuación, la función de densidad de probabilidad global f es solo la derivada de S con respecto al tiempo. (De nuevo, si el tiempo es discreto, f es sólo la suma de algunas funciones delta).,341fa8b2″>
Esto significa que si conocemos la función de Riesgo, podemos resolver esta ecuación diferencial para S:
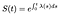
Si el tiempo es discreto, la integral de una suma de funciones delta sólo se convierte en una suma de los peligros en cada tiempo discreto.,
bien, eso resume la notación y los conceptos básicos que necesitaremos. Pasemos a discutir modelos.
modelos no-, Semi-y totalmente paramétricos
como dije anteriormente, normalmente estamos interesados en modelar la tasa de riesgo λ.
en un modelo no paramétrico, no hacemos suposiciones sobre la forma funcional de λ. La curva de Kaplan–Meier es el Estimador de máxima verosimilitud en este caso. La desventaja es que esto hace que sea difícil modelar los efectos de las covariables. Es un poco como usar un gráfico de dispersión para entender el efecto de una covariable., No necesariamente tan útil como un modelo totalmente paramétrico como una regresión lineal.
en un modelo completamente paramétrico, hacemos una suposición para la forma funcional precisa de λ. Una discusión de los modelos completamente paramétricos es un artículo completo por derecho propio, pero vale la pena una discusión muy breve. La siguiente tabla muestra tres de los modelos completamente paramétricos más comunes. Cada uno es generalizado por el siguiente, pasando de 1 a 2 a 3 parámetros. La forma funcional de la función de peligro se muestra en la columna central. El logaritmo de la función hazard también se muestra en la última columna., Se asume que todos los parámetros (ɣ, α, μ) son positivos, excepto que μ podría ser 0 en la distribución de Weibull generalizada (reproduciendo la distribución de Weibull).

Mirando el logaritmo nos muestra que el modelo exponencial se supone que la función de riesgo es constante. El modelo Weibull asume que está aumentando si α> 1, constante si α = 1, y disminuyendo si α<1., El modelo de Weibull generalizado comienza de la misma manera que el modelo de Weibull (al principio ln S = 0). Después de eso, un término extra μ entra en acción.
el problema con estos modelos es que hacen suposiciones fuertes sobre los datos. En ciertos contextos, puede haber razones para creer que estos modelos encajan bien. Pero con estas y varias otras opciones disponibles, existe un fuerte riesgo de sacar conclusiones incorrectas debido a la falta de especificación del modelo.
Esta es la razón por la que Cox Proportional Hazards, un modelo semi-paramétrico, es tan popular., No se hacen suposiciones funcionales sobre la forma de la función de peligro; en cambio, se hacen suposiciones de forma funcional sobre los efectos de las covariables por sí solas.,
La Cox de Riesgos Proporcionales de Modelo
el Modelo de Riesgos Proporcionales de Cox se da normalmente en términos del tiempo t, covariable vector x, y el coeficiente del vector β como
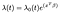
donde el λₒ es una función arbitraria de tiempo, la línea de base de peligro. El producto escalar de X y β se toma en el exponente al igual que en la regresión lineal estándar., Independientemente de los valores covariables, todos los sujetos comparten el mismo riesgo basal λₒ. A partir de entonces, se realizan ajustes basados en las covariables.
interpretación de los resultados
Supongamos por minuto que hemos ajustado un modelo de riesgos proporcionales de Cox a nuestros datos, que consistió en
- Una columna especificando el tiempo para cada sujeto
- Una columna especificando si el sujeto fue «observado» (haber fallado, o, en nuestro ejemplo preferido, tener su progreso de la enfermedad). Un valor de 1 significa que el sujeto tenía su progreso de la enfermedad., Un valor de 0 significa que, en el último momento de observación, la enfermedad no había progresado. La observación fue censurada.
- columnas para nuestras covariables X.
Después del ajuste, obtendremos valores Para β. Por ejemplo, supongamos por simplicidad que hay una sola covariable. Un valor de β=0.1 significa que un aumento en la covariable en una cantidad de 1 conduce a un aproximadamente 10% de alta probabilidad de progresión de la enfermedad en un momento dado., El valor exacto es, de hecho,

Para valores pequeños de β, el valor de β sí es una muy buena aproximación de la exacta aumento de riesgo. Para valores mayores de β, se debe calcular la cantidad exacta.
otra forma de expresar β = 0.1 es que, a medida que X aumenta, el riesgo aumenta a una tasa de 10% por aumento de x en 1. El 10 más grande.,El 52% surge de la composición (continua), al igual que con el interés compuesto.
Además, β = 0 significa que no hay efecto, y β negativo significa que hay menos riesgo a medida que aumenta la covariable. Tenga en cuenta que, a diferencia de las regresiones estándar, no hay término de intercepción. En su lugar, la intercepción es absorbida por el peligro de línea de base λₒ, que también se puede estimar (véase más adelante).
finalmente, asumiendo que hemos estimado la función de riesgo basal, podemos construir la función de sobreviviente.,
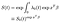
La función de línea de base es elevado a la potencia de la exp(xʹß) factor procedentes de las covariables. Se debe tener cierto cuidado al interpretar la función basal del sobreviviente, que juega aproximadamente el papel del término de intercepción en una regresión lineal regular. Si las covariables se han centrado (media 0), entonces representa la función sobreviviente para el sujeto «promedio».,
estimación del modelo de riesgos proporcionales de Cox
en la década de 1970, David Cox, un matemático británico, propuso una forma de estimar β sin tener que estimar el riesgo basal λₒ. Una vez más, el peligro de referencia puede estimarse posteriormente. Como se mencionó anteriormente, veremos que es el ordenamiento de los fracasos observados lo que importa, no los tiempos mismos.
antes de saltar a la estimación, vale la pena discutir los lazos. Dado que normalmente solo observamos datos en incrementos discretos, es posible que dos fallas ocurran al mismo tiempo., Por ejemplo, dos máquinas pueden fallar en la misma semana y la grabación solo se realiza semanalmente. Estos vínculos hacen que el análisis de la situación sea bastante complicado sin agregar mucha información. En consecuencia, derivaré las estimaciones en el caso de que no haya vínculos.
recuerde que nuestros datos consisten en observaciones de algunos fallos numéricos en un tiempo discreto. Que R (t) denote la población «en riesgo» en el tiempo t. si un sujeto en nuestro estudio ha fallado (la enfermedad progresó, por ejemplo) antes del tiempo t, no están «en riesgo».,»Además, si un sujeto en nuestro estudio ha tenido su observación censurada en un momento antes del tiempo t, tampoco están en riesgo.»
de la manera habitual, queremos construir una función de verosimilitud (Cuál es la probabilidad que habríamos observado los datos que hicimos, dadas las covariables y coeficientes) y luego optimizarla para obtener un estimador de máxima verosimilitud.
para cada tiempo discreto en que observamos un fallo del sujeto j, la probabilidad de que ocurra, dado que se produjo un fallo, está por debajo. La suma se toma sobre todos los sujetos en riesgo en el momento j.,

Observe que la línea de base de peligro λₒ ha caído! Muy conveniente. Por esta razón, la probabilidad que construimos es solo una probabilidad parcial. Observe también que los tiempos no aparecen en absoluto., El término para Sujeto j depende solo de qué sujetos están vivos en el momento j, que a su vez depende solo del orden en el que los sujetos son censurados u observados para fallar.
la probabilidad parcial es, por supuesto, solo el producto de estos Términos, uno por cada falla que observamos (no hay términos para observaciones censuradas).,
el log de verosimilitud parcial es entonces
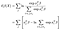
ecuación 2) función de log verosimilitud parcial
el ajuste se realiza con métodos numéricos estándar, por ejemplo en el paquete python statsmodels y la matriz de varianza-covarianza para las estimaciones viene dada por la matriz de información de Fisher (inversa de la). Nada emocionante aquí.,
estimar la función basal del Sobreviviente
ahora que hemos estimado los coeficientes, podemos estimar la función del sobreviviente. Esto termina siendo muy similar a estimar una curva de Kaplan-Meier.
postulamos términos α indexados por i. en el tiempo i, la curva basal del sobreviviente debe disminuir en una fracción α que representa la proporción de sujetos en riesgo que fallan en el tiempo i., En otras palabras
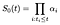
para calcular el estimador de máxima verosimilitud Para α, consideramos la contribución de verosimilitud del sujeto i que falla en el tiempo I y por separado la contribución de aquellos que son censurados en el tiempo i.
para un sujeto que falla en el tiempo i, la probabilidad está dada por la probabilidad de que estén vivos en el tiempo I menos la probabilidad de que estén vivos en la próxima vez I+1. (Asumimos temporalmente que los tiempos están ordenados).,
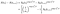
Si por el contrario son censurados en el tiempo yo, la contribución es sólo la probabilidad de que estén vivos en el momento después que yo, es decir, que no han muerto todavía., Esto es sólo
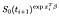
Hay un plazo adicional de los temas que se han observado (es decir, observó a fallar en lugar de censura)., La probabilidad de registro se convierte en
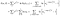
ecuación 5) log likelihood for the baseline Survivor function
he sido un poco descuidado sobre el seguimiento de los puntos finales (i VS.i+1), pero todo funcionará.
solo hay términos α para los sujetos que observamos fallar., Diferenciando con respecto a α-j y suponiendo que no hay lazos, obtenemos una contribución de la suma de la izquierda solo para los sujetos vivos en el tiempo j, y una sola contribución del término a la derecha.,qual a 0 significa que podemos obtener las estimaciones de máxima verosimilitud Para α usando nuestras estimaciones Para β Como la solución a las varias ecuaciones, una para cada sujeto que se observó que fallaba:
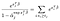
extensiones y advertencias
hay mucho más que decir sobre los modelos de riesgos proporcionales de Cox, pero trataré de mantener las cosas breves y solo mencionaré algunas cosas.,
por ejemplo, uno puede querer considerar regresores variables en el tiempo, y esto es posible.
la otra cosa crucial a tener en cuenta es el sesgo variable omitido. En la regresión lineal estándar, las variables omitidas no correlacionadas con los regresores no son un gran problema. Esto no es cierto en el análisis de supervivencia. Supongamos que tenemos dos subpoblaciones de igual tamaño y muestreadas en nuestros datos, cada una con una tasa de riesgo constante, una es 0.1 y la otra es 0.5. Inicialmente, veremos una alta tasa de riesgo (El promedio, solo 0.3)., A medida que pasa el tiempo, la población con una alta tasa de riesgo abandonará la población y observaremos una tasa de riesgo que disminuye hacia 0.1. Si omitimos la variable que representa a estas dos poblaciones, nuestra tasa de riesgo de referencia será todo desordenado.