El coeficiente α es el procedimiento más utilizado para estimar la confiabilidad en la investigación aplicada. Como afirma Sijtsma (2009), su popularidad es tal que Cronbach (1951) ha sido citado como referencia con más frecuencia que el artículo sobre el descubrimiento de la doble hélice del ADN., Sin embargo, sus limitaciones son bien conocidas (Lord y Novick, 1968; Cortina, 1993; Yang y Green, 2011), siendo algunas de las más importantes los supuestos de errores no correlacionados, Tau-equivalencia y normalidad.
el supuesto de errores no correlacionados (la puntuación de error de cualquier par de ítems no está correlacionada) es una hipótesis de la teoría de pruebas clásica (Lord y Novick, 1968), cuya violación puede implicar la presencia de estructuras multidimensionales complejas que requieren procedimientos de estimación que tengan en cuenta esta complejidad (por ejemplo, Tarkkonen y Vehkalahti, 2005; Green y Yang, 2015)., Es importante eliminar la creencia errónea de que el coeficiente α es un buen indicador de unidimensionalidad porque su valor sería mayor si la escala fuera unidimensional. De hecho, ocurre exactamente lo contrario, como lo demostró Sijtsma (2009), y su aplicación en tales condiciones puede llevar a una sobreestimación considerable de la fiabilidad (Raykov, 2001). En consecuencia, antes de calcular α es necesario comprobar que los datos se ajustan a modelos unidimensionales.
el supuesto de Tau-equivalencia (i. e.,, la misma puntuación verdadera para todos los elementos de prueba, o cargas factoriales iguales de todos los elementos en un modelo factorial) es un requisito Para Que α sea equivalente al coeficiente de confiabilidad (Cronbach, 1951). Si se viola la suposición de equivalencia tau, el verdadero valor de confiabilidad será subestimado (Raykov, 1997; Graham, 2006) en una cantidad que puede variar entre 0.6 y 11.1% dependiendo de la gravedad de la violación (Green y Yang, 2009a). Trabajar con datos que cumplan con este supuesto generalmente no es viable en la práctica( Teo y Fan, 2013); el modelo congénero (i. e.,, diferentes cargas de factores) es el más realista.
el requisito de normalidad multivariante es menos conocido y afecta tanto a la estimación de la confiabilidad puntual como a la posibilidad de establecer intervalos de confianza (Dunn et al., 2014). Sheng y Sheng (2012) observaron recientemente que cuando las distribuciones son sesgadas y/o leptocúrticas, se produce un sesgo negativo cuando se calcula el coeficiente α; resultados similares fueron presentados por Green y Yang (2009b) en un análisis de los efectos de las distribuciones no normales en la estimación de la confiabilidad., El estudio de los problemas de asimetría es más importante cuando vemos que en la práctica los investigadores habitualmente trabajan con escalas asimétricas (Micceri, 1989; Norton et al., 2013; Ho y Yu, 2014). Por ejemplo, Micceri (1989) estimó que aproximadamente 2/3 de la capacidad y más de 4/5 de las medidas psicométricas exhibían al menos asimetría moderada (es decir, asimetría alrededor de 1). A pesar de esto, el impacto de la asimetría en la estimación de la confiabilidad ha sido poco estudiado.,
considerando la abundante literatura sobre las limitaciones y sesgos del coeficiente α (Revelle y Zinbarg, 2009; Sijtsma, 2009, 2012; Cho y Kim, 2015; sijtsma y van der Ark, 2015), surge la pregunta de por qué los investigadores continúan utilizando α cuando existen coeficientes alternativos que superan estas limitaciones. Es posible que el exceso de procedimientos para estimar la confiabilidad desarrollado en el siglo pasado haya oscurecido el debate. Esto se habría visto agravado por la simplicidad del cálculo de este coeficiente y su disponibilidad en los programas informáticos comerciales.,
la dificultad de estimar el’ coeficiente de confiabilidad PXX reside en su definición PXX’=σt2 σ σx2, que incluye el puntaje verdadero en el numerador de varianza cuando esto es por naturaleza no observable. El coeficiente α intenta aproximar esta varianza no observable a partir de la covarianza entre los elementos o componentes. Cronbach (1951) mostró que en ausencia de equivalencia tau, el coeficiente α (O lambda 3 de Guttman, que es equivalente a α) era una buena aproximación de límite inferior., Así, cuando se violan los supuestos, el problema se traduce en encontrar el mejor límite inferior posible; de hecho, este nombre se le da al método de mayor límite inferior (GLB) que es la mejor aproximación posible desde un ángulo teórico (Jackson y Agunwamba, 1977; Woodhouse y Jackson, 1977; Shapiro y ten Berge, 2000; Sočan, 2000; ten Berge y Sočan, 2004; Sijtsma, 2009). Sin embargo, Revelle y Zinbarg (2009) consideran que ω da un límite inferior mejor que GLB., Por lo tanto, hay un debate sin resolver sobre cuál de estos dos métodos da el mejor límite inferior; además, la cuestión de la no normalidad no se ha investigado exhaustivamente, como se discute en el presente trabajo.
coeficientes ω
McDonald (1999) propuso el coeficiente wt para estimar la confiabilidad a partir de un marco de análisis factorial, que puede expresarse formalmente como:
donde λj es la carga del ítem j, λj2 es la comunalidad del ítem j y ψ equivale a la unicidad., El coeficiente wt, al incluir los lambdas en sus fórmulas, es adecuado tanto cuando existe equivalencia tau (es decir, cargas factoriales iguales de todos los elementos de prueba) (wt coincide matemáticamente con α), Como cuando hay elementos con diferentes discriminaciones presentes en la representación del constructo (es decir, cargas factoriales diferentes de los elementos: mediciones congéneras). En consecuencia, wt corrige el sesgo de subestimación de α cuando se viola la suposición de equivalencia tau (Dunn et al., 2014) y diferentes estudios muestran que es una de las mejores alternativas para estimar la confiabilidad (Zinbarg et al.,, 2005, 2006; Revelle y Zinbarg, 2009), aunque hasta la fecha se desconoce su funcionamiento en condiciones de asimetría.
cuando existe correlación entre errores, o hay más de una dimensión latente en los datos, se estima la contribución de cada dimensión a la varianza total explicada, obteniendo el llamado ω jerárquico (wh) que nos permite corregir el peor sesgo de sobreestimación de α con datos multidimensionales (ver Tarkkonen y Vehkalahti, 2005; Zinbarg et al., 2005; Revelle y Zinbarg, 2009)., Los coeficientes wh y wt son equivalentes en datos unidimensionales, por lo que nos referiremos a este coeficiente simplemente como ω.
mayor límite inferior (GLB)
Sijtsma (2009) muestra en una serie de estudios que uno de los estimadores más poderosos de la confiabilidad es GLB—deducido por Woodhouse y Jackson (1977) a partir de los supuestos de la teoría de pruebas clásica (Cx = Ct + Ce)—una matriz de covarianza inter-ítem para los puntajes de ítem observados Cx. Se divide en dos partes: la suma de la matriz de covarianza entre ítems para puntajes verdaderos de ítems Ct; y la matriz de covarianza de error entre ítems Ce (ten Berge y Sočan, 2004)., Su expresión es:
donde σx2 es la varianza de la prueba y tr(Ce) se refiere a la traza de la matriz de covarianza de error entre ítems que ha demostrado ser tan difícil de estimar. Una solución ha sido utilizar procedimientos factoriales como el Análisis Factorial de Rango mínimo (un procedimiento conocido como glb).fa). Más recientemente, el procedimiento algebraico GLB (GLBa) se ha desarrollado a partir de un algoritmo ideado por Andreas Moltner (Moltner y Revelle, 2015)., Según Revelle (2015a) este procedimiento adopta la forma más fiel a la definición original de Jackson y Agunwamba (1977), y tiene la ventaja añadida de introducir un vector para ponderar los ítems por importancia (Al-Homidan, 2008).
a pesar de sus fortalezas teóricas, GLB ha sido muy poco utilizado, aunque algunos estudios empíricos recientes han demostrado que este coeficiente produce mejores resultados Que α (Lila et al., 2014) y α y ω (Wilcox et al., 2014)., Sin embargo, en muestras pequeñas, bajo el supuesto de normalidad, tiende a sobreestimar el verdadero valor de confiabilidad (Shapiro y ten Berge, 2000); sin embargo, su funcionamiento en condiciones no normales sigue siendo desconocido, específicamente cuando las distribuciones de los ítems son asimétricas.
considerando los coeficientes definidos anteriormente, y los sesgos y limitaciones de cada uno, el objeto de este trabajo es evaluar la robustez de estos coeficientes en presencia de ítems asimétricos, considerando también el supuesto de Tau-equivalencia y el tamaño de la muestra.,
métodos
generación de datos
los datos se generaron utilizando el software R (R Development Core Team, 2013) y RStudio (Racine, 2012), siguiendo el modelo factorial:
IJ es la respuesta simulada del sujeto I en el ítem J, λjk es la carga del ítem j en el factor K (que fue generado por el modelo unifactorial); FK es el factor latente generado por una distribución normal estandarizada (Media 0 y varianza 1), y ej es el error de medición Aleatorio de cada ítem también siguiendo una distribución normal estandarizada.,
elementos sesgados: los Xij normales estándar se transformaron para generar distribuciones no normales utilizando el procedimiento propuesto por Headrick (2002) aplicando transformaciones polinómicas de quinto orden:
condiciones simuladas
para evaluar el rendimiento de la fiabilidad coeficientes (α, ω, Glb y GLBA) se trabajó con tres tamaños de muestra (250, 500, 1000), dos tamaños de prueba: corto (6 ítems) y largo (12 ítems), dos condiciones de equivalencia tau (una con equivalencia Tau y otra sin, i. e.,, congéneres) y la incorporación progresiva de elementos asimétricos (desde todos los elementos normales a todos los elementos asimétricos). En la prueba corta la confiabilidad se fijó en 0,731, que en presencia de Tau-equivalencia se logra con seis ítems con cargas factoriales = 0,558; mientras que el modelo congénero se obtiene fijando cargas factoriales en valores de 0.3, 0.4, 0.5, 0.6, 0.7, y 0.8 (véase el Apéndice I). En la prueba larga de 12 ítems la confiabilidad se fijó en 0.,845 tomando los mismos valores que en la prueba corta tanto para la equivalencia tau como para el modelo congénero (en este caso hubo dos ítems para cada valor de lambda). De esta manera se simularon 120 condiciones con 1000 réplicas en cada caso.
análisis de datos
los principales análisis se realizaron utilizando los paquetes Psych (Revelle, 2015b) y GPArotation (Bernaards y Jennrich, 2015), que permiten estimar α y ω. Se utilizaron dos enfoques computarizados para estimar GLB: glb.fa (Revelle, 2015a) y glb.,algebraico (Moltner y Revelle, 2015), este último trabajado por autores como Hunt y Bentler (2015).
con el fin de evaluar la precisión de los diversos estimadores en la recuperación de la confiabilidad, se calculó la raíz media cuadrada de Error (RMSE) y el sesgo. La primera es la media de las diferencias entre la fiabilidad estimada y la simulada y se formaliza como:
donde ρ^ es la fiabilidad estimada para cada coeficiente, ρ la fiabilidad simulada y Nr el número de réplicas., El sesgo % se entiende como la diferencia entre la media de la confiabilidad estimada y la confiabilidad simulada y se define como:
en ambos índices, cuanto mayor es el valor, mayor es la inexactitud del estimador, pero a diferencia de RMSE, el sesgo puede ser positivo o negativo; en este caso se obtendría información adicional sobre si el coeficiente está subestimando o sobreestimando el parámetro de confiabilidad simulada., Siguiendo la recomendación de Hoogland y Boomsma (1998) se consideraron aceptables los valores de RMSE < 0,05 y % bias < 5%.
resultados
los principales resultados pueden verse en la tabla 1 (6 ítems) y en la Tabla 2 (12 ítems). Estos muestran el RMSE y el sesgo % de los coeficientes en Tau-equivalencia y condiciones congéneras, y cómo la asimetría de la distribución de la prueba aumenta con la incorporación gradual de ítems asimétricos.
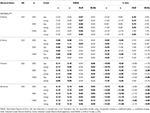
la Tabla 1., RMSE y sesgo con equivalencia tau y condición congénera para 6 ítems, tres tamaños de muestra y el número de ítems sesgados.
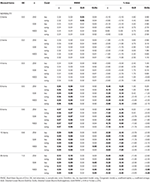
la Tabla 2. RMSE y sesgo con equivalencia tau y condición congénera para 12 ítems, tres tamaños de muestra y el número de ítems sesgados.
solo bajo condiciones de equivalencia tau y normalidad (asimetría < 0.2) se observa que el coeficiente α estima correctamente la confiabilidad simulada, como ω., En el congenéricas condición ω corrige la subestimación de α. Tanto GLB como GLBa presentan un sesgo positivo bajo normalidad, sin embargo GLBa muestra aproximadamente ½ % menos sesgo que GLB (Ver Tabla 1). Si consideramos el tamaño de la muestra, observamos que a medida que aumenta el tamaño de la prueba, el sesgo positivo de GLB y GLBa disminuye, pero nunca desaparece.
en condiciones asimétricas, vemos en la tabla 1 que tanto α Como ω presentan un rendimiento inaceptable con RMSE creciente y subestimaciones que pueden alcanzar sesgo > 13% para el coeficiente α (entre 1 y 2% Menor Para ω)., Los coeficientes GLB y GLBa presentan menor RMSE cuando aumenta la asimetría de la prueba o el número de ítems asimétricos (Ver tablas 1, 2). El coeficiente GLB presenta mejores estimaciones cuando el valor de asimetría de la prueba es alrededor de 0.30; GLBa es muy similar, presentando mejores estimaciones Que ω con un valor de asimetría de la prueba alrededor de 0.20 o 0.30. Sin embargo, cuando el valor de asimetría aumenta a 0.50 o 0.60, GLB presenta un mejor rendimiento que GLBa. El tamaño de la prueba (6 o 12 ítems) tiene un efecto mucho más importante que el tamaño de la muestra en la precisión de las estimaciones.,
discusión
en este estudio se manipularon cuatro factores: Tau-equivalencia o modelo congénero, tamaño muestral (250, 500 y 1000), Número de ítems de prueba (6 y 12) y número de ítems asimétricos (desde 0 ítems asimétricos hasta todos los ítems asimétricos) para evaluar la robustez a la presencia de datos asimétricos en los cuatro coeficientes de confiabilidad analizados. Estos resultados se analizan a continuación.,
en condiciones de equivalencia tau, los coeficientes α y ω convergen, sin embargo en ausencia de equivalencia tau (congénera), ω siempre presenta mejores estimaciones y menor RMSE y sesgo % que α. Por lo tanto, en esta condición más realista (Green y Yang, 2009a; Yang y Green, 2011), α se convierte en un estimador de confiabilidad sesgado negativamente (Graham, 2006; Sijtsma, 2009; Cho y Kim, 2015) y ω es siempre preferible a α (Dunn et al., 2014). En el caso de no violación del supuesto de normalidad, ω es el mejor estimador de todos los coeficientes evaluados (Revelle y Zinbarg, 2009).,
volviendo al tamaño de la muestra, observamos que este factor tiene un pequeño efecto bajo la normalidad o un ligero alejamiento de la normalidad: el RMSE y el sesgo disminuyen a medida que aumenta el tamaño de la muestra. Sin embargo, se puede decir que para estos dos coeficientes, con tamaño muestral de 250 y normalidad se obtienen estimaciones relativamente precisas (Tang y Cui, 2012; Javali et al., 2011)., Para los coeficientes GLB y GLBa, a medida que el tamaño de la muestra aumenta el RMSE y el sesgo tiende a disminuir; sin embargo, mantienen un sesgo positivo para la condición de normalidad incluso con grandes tamaños de muestra de 1000 (Shapiro y ten Berge, 2000; ten Berge y Sočan, 2004; Sijtsma, 2009).
para el tamaño de la prueba Generalmente observamos un RMSE y sesgo más altos con 6 ítems que con 12, lo que sugiere que cuanto mayor es el número de ítems, menor es el RMSE y el sesgo de los estimadores (Cortina, 1993). En general, la tendencia se mantiene para 6 y 12 partidas.,
cuando observamos el efecto de incorporar progresivamente elementos asimétricos en el conjunto de datos, observamos que el coeficiente α es altamente sensible a elementos asimétricos; estos resultados son similares a los encontrados por Sheng y Sheng (2012) y Green y Yang (2009b). El coeficiente ω presenta valores de RMSE y sesgo similares a los de α, pero ligeramente mejores, incluso con equivalencia tau. GLB y GLBa presentan mejores estimaciones cuando la asimetría de la prueba se aparta de valores cercanos a 0.
Considerando que en la práctica es común encontrar datos asimétricos (Micceri, 1989; Norton et al.,, 2013; Ho y Yu, 2014), la sugerencia de Sijtsma (2009) de usar GLB como estimador de confiabilidad parece bien fundada. Otros autores, como Revelle y Zinbarg (2009) y Green y Yang (2009a), recomiendan el uso de ω, Sin embargo este coeficiente solo produjo buenos resultados en la condición de normalidad, o con baja proporción de ítems de asimetría. En cualquier caso, estos coeficientes presentaron mayores ventajas teóricas y empíricas que α. Sin embargo, recomendamos a los investigadores estudiar no solo estimaciones puntuales, sino también hacer uso de la estimación de intervalos (Dunn et al., 2014).,
estos resultados se limitan a las condiciones simuladas y se asume que no hay correlación entre errores. Esto obligaría a realizar nuevas investigaciones para evaluar el funcionamiento de los diversos coeficientes de fiabilidad con estructuras multidimensionales más complejas (Reise, 2012; Green y Yang, 2015) y en presencia de datos ordinales y/o categóricos en los que el incumplimiento del supuesto de normalidad es la norma.
conclusión
Cuando los puntajes Totales de las pruebas se distribuyen normalmente (p.ej.,, todos los elementos se distribuyen normalmente) ω debe ser la primera opción, seguido de α, ya que evitan los problemas de sobreestimación presentados por GLB. Sin embargo, cuando hay una asimetría de prueba baja o moderada, se debe usar GLBa. El GLB se recomienda cuando la proporción de ítems asimétricos es alta, ya que bajo estas condiciones no es aconsejable el uso de α y ω Como estimadores de confiabilidad, cualquiera que sea el tamaño de la muestra.
contribuciones de los autores
desarrollo de la idea de investigación y marco teórico (IT, JA). Construcción del marco metodológico (IT, JA)., Desarrollo de la sintaxis del lenguaje R (IT, JA). Análisis e interpretación de datos (IT, JA). Discusión de los resultados a la luz de los antecedentes teóricos actuales (JA, IT). Preparación y redacción del artículo (JA, IT). En general, ambos autores han contribuido igualmente al desarrollo de este trabajo.,
financiación
el primer autor informó haber recibido el siguiente apoyo financiero para la investigación, autoría y/o publicación de este artículo: recibió apoyo financiero de la Comisión Nacional de Investigaciones Científicas y tecnológicas de Chile (Conicyt) programa de Becas de Doctorado «Becas Chile» (beca no: 72140548).
Declaración de conflicto de intereses
los autores declaran que la investigación se realizó en ausencia de relaciones comerciales o financieras que pudieran ser interpretadas como un potencial conflicto de intereses.Cronbach, L. (1951)., Coeficiente alfa y la estructura interna de las pruebas. Psychometrika 16, 297-334. doi: 10.1007/BF02310555
CrossRef Full Text / Google Scholar
McDonald, R. (1999). Test Theory: A Unified Treatment (en inglés). Mahwah, NJ: Lawrence Erlbaum Associates.
Google Scholar
r development Core Team (2013). R: un lenguaje y entorno para la Computación estadística. Viena: R Foundation for Statistical Computing.Raykov, T. (1997)., Scale reliability, cronbach»s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package «psych.,»Available online at: http://org/r/psych-manual.pdf
Shapiro, A., and ten Berge, J. M. F. (2000). El sesgo asintótico del análisis de factor de traza mínimo, con aplicaciones al límite inferior más alto de confiabilidad. Psychometrika 65, 413-425. doi: 10.1007/BF02296154
CrossRef Full Text / Google Scholar
ten Berge, J. M. F., and Sočan, G. (2004). El mayor límite inferior a la fiabilidad de una prueba y la hipótesis de unidimensionalidad. Psychometrika 69, 613-625. doi: 10.,1007/BF02289858
CrossRef Full Text/Google Scholar
Woodhouse, B., and Jackson, P. H. (1977). Límites inferiores para la confiabilidad del puntaje total en una prueba compuesta por ítems no homogéneos: II: un procedimiento de búsqueda para localizar el límite inferior mayor. Psychometrika 42, 579-591. doi: 10.1007/BF02295980
CrossRef Full Text / Google Scholar
Appendix I
sintaxis R para estimar los coeficientes de confiabilidad de las matrices de correlación de Pearson., Los valores de correlación fuera de la diagonal se calculan multiplicando la carga factorial de los elementos: (1) modelo equivalente tau Todos son iguales a 0.3114 (λiλj = 0.558 × 0.558 = 0.3114) y (2) Modelo congénero varían en función de la carga factorial diferente (por ejemplo, el elemento de la matriz a1, 2 = λ1λ2 = 0.3 × 0.4 = 0.12). En ambos ejemplos la verdadera fiabilidad es de 0,731.
> omega(Cr,1)$alfa # estandarizado de Cronbach»s α
0.731
> omega(Cr,1)$de omega.tot # coeficiente ω total
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach»s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731