«I, en cualquier caso, Estoy convencido de que él no lanza dados.,»
~ Albert Einstein
- Variables Aleatorias
- Discretas Variables Aleatorias
- Continuo de Variables Aleatorias
- Mezclado Variables Aleatorias
- Funciones de Distribución Acumulativa (CDF)
- Función de Densidad de Probabilidad (PDF)
- Interactivo de CDF/PDF Ejemplo
Variables Aleatorias:

Dicen que fueron a tomar una moneda de su bolsillo y lo sacude en el aire. Mientras se mueve por el espacio, ¿qué podrías decir sobre su futuro?
¿aterrizará heads up? ¿Cruz?, Más que eso, ¿cuánto tiempo permanecerá en el aire? ¿Cuántas veces rebotará? ¿Qué tan lejos de donde primero golpea el suelo finalmente llegará a descansar? Para el caso, ¿alguna vez tocará el suelo? ¿Has venido a descansar?
para algunas de estas preguntas, podemos y nos conformamos con respuestas mucho antes de las observaciones; estamos bastante seguros de que la gravedad se mantendrá y la moneda aterrizará. Pero para otros no tenemos más remedio que juzgar y hablar en términos más vagos, si queremos decir algo útil sobre el futuro.,
Como científicos, es, por supuesto, nuestro trabajo decir algo útil (o, al menos, autoritaria…), mientras que las monedas metafóricas del sistema físico importante todavía están en el aire. Cara o cruz puede ser incluso una cuestión de vida o muerte. Nuestras monedas pueden ser, por ejemplo, varios posibles caudales de refrigerante o masas de uranio en una planta de energía nuclear. Nos importa mucho saber cuáles son nuestras posibilidades de que tengamos turbinas zumbantes en lugar de una fusión.,
para un determinista estricto, todas estas apuestas se liquidaron mucho antes de que se acuñara alguna moneda, metafórica o no; simplemente no lo sabemos todavía. Si supiéramos las fuerzas aplicadas en el lanzamiento de una moneda, su distribución exacta de la masa, los diversos movimientos diminutos de aire en la habitación… Si supiéramos todo eso, entonces sabríamos que ese lanzamiento de moneda en particular tiene un 100% de probabilidades de aterrizar de la manera en que aterrizará, y cero posibilidades de cualquier otro resultado.
pero, por supuesto, a menudo nos falta incluso una fracción mentionable de tal conocimiento del mundo., Además, parece que a escalas extremadamente pequeñas los deterministas estrictos están absolutamente equivocados; no hay manera de predecir cuándo, por ejemplo, un átomo de uranio se dividirá, y si tal evento afecta al mundo más grande, entonces ese evento macro es verdaderamente impredecible. Algunos resultados realmente están en el aire, sin resolver hasta que son parte del pasado.
para hacer frente a esta realidad y poder describir los estados futuros de un sistema de alguna manera útil, utilizamos variables aleatorias., Una variable aleatoria es simplemente una función que relaciona cada resultado físico posible de un sistema con un número real único. Como tal, hay tres tipos de variables aleatorias: discretas, continuas y mixtas. En las secciones siguientes se analizarán brevemente estas categorías y se darán ejemplos.
variables aleatorias discretas:
considere nuestro lanzamiento de moneda de nuevo. Podríamos tener cara o cruz como posibles resultados. Si definimos una variable, x, como el número de cabezas en un solo lanzamiento, entonces x podría ser 1 o 0, nada más., Tal función, x, sería un ejemplo de una variable aleatoria discreta. Tales variables aleatorias solo pueden tomar valores discretos. Otros ejemplos serían los posibles resultados de una prueba de embarazo, o el número de estudiantes en una sala de clase.
variables aleatorias continuas:
de vuelta al lanzamiento de la moneda, ¿qué pasaría si quisiéramos describir la distancia entre donde nuestra moneda se detuvo y donde cayó al suelo por primera vez? Esa distancia, x, sería una variable aleatoria continua porque podría tomar un número infinito de valores dentro del rango continuo de números reales., La moneda podía viajar 1 cm, o 1,1 cm, o 1,11 cm, o una y otra vez. Otros ejemplos de variables aleatorias continuas serían la masa de estrellas en nuestra galaxia, el pH de las aguas oceánicas o el tiempo de residencia de algún analito en un cromatógrafo de gases.
Variables aleatorias mixtas:
las variables aleatorias mixtas tienen componentes discretos y continuos. Tales variables aleatorias se encuentran con poca frecuencia. Para un posible ejemplo, sin embargo, puede estar midiendo el peso de una muestra y decidir que cualquier peso medido como un valor negativo se le dará un valor de 0., De esta manera, la variable aleatoria tiene un componente discreto en x = 0 y un componente continuo donde x > 0.
funciones de distribución acumulativa (CDF):
la pregunta, por supuesto, surge en cuanto a cómo describir matemáticamente (y mostrar visualmente) las variables aleatorias. Para esas tareas utilizamos funciones de densidad de probabilidad (PDF) y funciones de densidad acumulativa (CDF). Como los CDF son más fáciles de comprender para variables aleatorias discretas y continuas que los PDF, primero explicaremos los CDF.
considere lanzar un dado justo de 6 lados., Tendríamos una probabilidad de 1 en 6 de obtener cualquiera de los valores posibles de la variable aleatoria (1, 2, 3, 4, 5, ó 6). Si trazamos esos posibles valores en el eje x y trazamos la probabilidad de medir cada valor específico, x, o cualquier valor menor que x en el eje y, tendremos el CDF de la variable aleatoria.
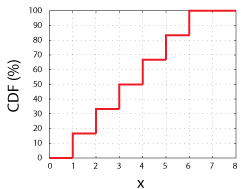
CDF for a Fair 6-Sidded Dice. Tenga en cuenta que cada paso tiene una altura de 16.67%, o 1 en 6.
Esta función, CDF (x), simplemente nos dice las probabilidades de medir cualquier valor hasta e incluyendo x., Como tal, todos los CDF deben tener estas características:
- Un CDF debe ser igual a 0 cuando x= -∞, y acercarse a 1 (o 100%) cuando x se aproxima a +∞. En pocas palabras, de todos los resultados posibles, debe haber un resultado; la probabilidad de lanzar un dado de seis lados y obtener un valor entre -∞ y ∞ es del 100%.
- la pendiente de un CDF siempre debe ser igual o mayor que cero. Por ejemplo, considere la posibilidad de lanzar un dado de 6 lados (justo o no) y obtener un valor entre 0 y 4., Esa posibilidad no puede ser más que la posibilidad de obtener un valor entre 0 y 5, porque las probabilidades de un 1, 2 o 3 de aterrizaje boca arriba son, por supuesto, siempre va a ser una fracción de las probabilidades de obtener un 1, 2, 3 o 4.
para un ejemplo de una variable aleatoria continua, el siguiente applet muestra la CDF normalmente distribuida.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Simplemente tenga en cuenta que las características de un CDF descritas anteriormente y explicadas para una variable aleatoria discreta también se mantienen para variables aleatorias continuas.
para obtener ejemplos más intuitivos de las propiedades de los CDF, consulte el ejemplo interactivo a continuación. También, las parcelas interactivas de muchos otros CDF importantes para el campo de las estadísticas y utilizados en este sitio se pueden encontrar aquí.
funciones de densidad de probabilidad (PDF):
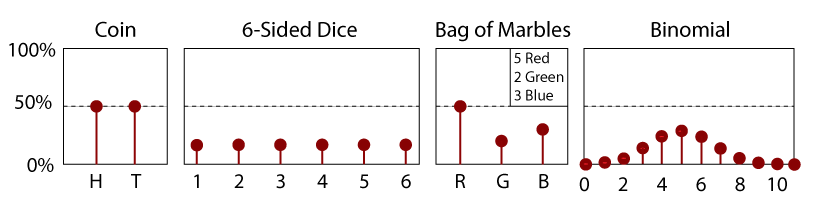
PDF para un dado justo de 6 lados.
un PDF es simplemente la derivada de un CDF., Por lo tanto, un PDF también es una función de una variable aleatoria, x, y su magnitud será una indicación de la probabilidad relativa de medir un valor particular. Como es la pendiente de un CDF, un PDF siempre debe ser positivo; no hay probabilidades negativas para ningún evento. Además, y por definición, el área bajo la curva de un PDF (x) entre – ∞ y x es igual a su CDF(x). Como tal, el área entre dos valores x1 y x2 da la probabilidad de medir un valor dentro de ese rango.
el siguiente applet muestra un ejemplo del PDF para una variable aleatoria normalmente distribuida, x.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., también considere la diferencia entre un PDF continuo y discreto. Mientras que un PDF discreto (como el que se muestra arriba para dice) le dará las probabilidades de obtener un resultado particular, las probabilidades con PDFs continuos son cuestiones de Rango, No puntos discretos. Por ejemplo, hay claramente una probabilidad de 1 en 6 (16.6%) de lanzar un 3 en un dado, como se puede ver en su PDF. Pero ¿cuáles son los impares de medir exactamente cero con una variable aleatoria que tiene un PDF normal y media de cero, como se muestra arriba? A pesar de que es el valor donde el PDF es el más grande, la posibilidad de medir exactamente 0.00000..,. es, tal vez contra intuitivamente, cero. Las probabilidades de medir cualquier número aleatorio en particular con precisión infinita son, de hecho, cero. con un PDF continuo, puede preguntar cuáles son las probabilidades de que medirá entre dos valores para obtener una probabilidad mayor que cero. Para encontrar esta probabilidad simplemente usamos el CDF de nuestra variable aleatoria., Debido a que el CDF nos dice la impar de medir un valor o algo menor que ese valor, para encontrar la probabilidad de medir entre dos valores, x1 y x2 (donde x1 > x2), simplemente tenemos que tomar el valor del CDF en x1 y restar de él el valor del CDF En x2. Por ejemplo, usando el CDF normal en el applet anterior (con μ=0, y σ=1), si deseábamos conocer las probabilidades de medir entre 0.01 y 0.02 encontramos CDF(x=0.1)=53.9828% Y CDF(x=0.2)=57.9260%. Entonces la diferencia, CDF(0.2)-CDF (0.1), nos da las probabilidades de aproximadamente 3.9% de medir una x entre 0.1 y 0.2., para obtener ejemplos más intuitivos y visuales de las propiedades de los PDF, consulte el ejemplo interactivo a continuación. También, las parcelas interactivas de muchos PDF importantes utilizados en este sitio se pueden ver aquí. |
|||||||||||||||||