
Pitágoras
hace más de 2000 años hubo un descubrimiento sorprendente sobre los triángulos:
Cuando un triángulo tiene un ángulo recto (90°) …
… y los cuadrados se hacen en cada uno de los tres lados, …
… ¡entonces el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos!,
se llama «Teorema de Pitágoras» y se puede escribir en una ecuación corta:
a2 + b2 = c2
nota:
- C es el lado más largo del triángulo
- A y B son los otros dos lados
definición
el lado más largo del triángulo se llama»hipotenusa», por lo que la definición formal es:
en un triángulo hipotenusa es igual a
la suma de los cuadrados de los otros dos lados.,
claro … ?
veamos si realmente funciona usando un ejemplo.

¿por Qué Es Útil?
si conocemos las longitudes de dos lados de un triángulo en ángulo recto, podemos encontrar la longitud del tercer lado. (Pero recuerde que solo funciona en triángulos en ángulo recto!)
¿Cómo lo Uso?,
Escribir como una ecuación:
 |
a2 + b2 = c2 |
a Continuación, se utiliza el álgebra para encontrar cualquier valor que falta, como en estos ejemplos:
también puede leer acerca de Cuadrados y Raíces Cuadradas para averiguar por qué √169 = 13
funciona de la otra manera alrededor, demasiado: cuando los tres lados de un triángulo hacer a2 + b2 = c2, entonces el triángulo es rectángulo.,
y puede probar el Teorema usted mismo !
obtener papel pluma y tijeras, a continuación, utilizando la siguiente animación como guía:
- dibujar un triángulo en ángulo recto en el papel, dejando un montón de espacio.,
- dibuja un cuadrado a lo largo de la hipotenusa (el lado más largo)
- dibuja un cuadrado del mismo tamaño en el otro lado de la hipotenusa
- dibuja líneas como se muestra en la animación, así:

- recorta las formas
- Arréglalas para que puedas probar que el cuadrado grande tiene la misma área que los dos cuadrados en los otros lados
otro, increíblemente simple, prueba
Aquí está una de las pruebas más antiguas de que el cuadrado en el lado largo tiene la misma área que los otros cuadrados.,
mira la animación y presta atención cuando los triángulos empiecen a deslizarse.
es posible que desee ver la animación un par de veces para entender lo que está sucediendo.
el triángulo púrpura es el importante.
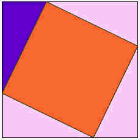 |
se convierte en | 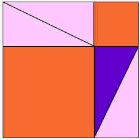 |

