8.1 un ejemplo histórico
en su libro, Las dos nuevas ciencias, Galileo Galilea (1564-1642) da varios argumentos destinados a demostrar que no puede haber tal cosa como infinitos reales o infinitesimales reales. Uno de sus argumentos puede ser reconstruido de la siguiente manera. Galileo propone que tomemos como premisa que hay una infinidad real de números naturales (los números naturales son los números enteros positivos a partir de 1):
{1, 2, 3, 4, 5, 6, 7, ….,}
también propone que tomemos como premisa que hay una infinidad real de los cuadrados de los números naturales.
{1, 4, 9, 16, 25, 36, 49, ….}
Ahora, Galileo razona, tenga en cuenta que estos dos grupos (hoy los llamaríamos «conjuntos») tienen el mismo tamaño. Podemos ver esto porque podemos ver que hay una correspondencia uno-a-uno entre los dos grupos.,
| {1, | 2, | 3, | 4, | 5, | 6, | 7, ….,div> | |
| {1, | 4, | 9, | 16, | 25, | 36, | 49, …} |
Si se puede asociar a cada número natural con uno y sólo un número cuadrado, y si se puede asociar cada número cuadrado con uno y sólo un número natural, entonces estos deben ser del mismo tamaño.,
pero espera un momento, dice Galileo. Obviamente hay muchos más números naturales que números cuadrados. Es decir, cada número cuadrado está en la lista de números naturales, pero muchos de los números naturales no están en la lista de números cuadrados. Los siguientes números están todos en la lista de números naturales pero no en la lista de números cuadrados.
{2, 3, 5, 6, 7, 8, 10, ….,}
entonces, Galileo razona, si hay muchos números en el grupo de números naturales que no están en el grupo de los números cuadrados, y si no hay números en el grupo de los números cuadrados que no están en los números naturales, entonces los números naturales son más grandes que los números cuadrados. Y si el grupo de los números naturales es más grande que el grupo de los números cuadrados, entonces los números naturales y los números cuadrados no son del mismo tamaño.,
hemos llegado a dos conclusiones: el conjunto de los números naturales y el conjunto de los números cuadrados son del mismo tamaño; y, el conjunto de los números naturales y el conjunto de los números cuadrados no son del mismo tamaño. Eso es contradictorio.
Galileo argumenta que la razón por la que llegamos a una contradicción es porque asumimos que hay infinidades reales. Concluye, por lo tanto, que no hay infinidades reales.
8.2 pruebas indirectas
nuestra lógica todavía no es lo suficientemente fuerte como para probar algunos argumentos válidos. Considere el siguiente argumento como ejemplo.,
(P→(QvR))
Q
I
P
Este argumento parece válido. Por la primera premisa sabemos: si P fuera verdad, entonces también sería verdad (Q v R). Pero entonces Q O R o ambos serían verdaderos. Y por la segunda y tercera premisas sabemos: Q es falso y R es falso. Así que no puede ser que (Q v R) sea verdad, y así no puede ser que P sea verdad.
podemos comprobar el argumento usando una tabla de verdad. Nuestra mesa será compleja porque una de nuestras premisas es compleja.,
In any kind of situation in which all the premises are true, the conclusion is true., Es decir: las premisas son todas verdaderas solo en la última fila. Para esa fila, la conclusión también es cierta. Por lo tanto, este es un argumento válido.
pero tómese un minuto y trate de probar este argumento. Empezamos con el

Y ahora nos hemos parado. No podemos aplicar ninguna de nuestras reglas. Aquí hay un argumento válido que no hemos hecho que nuestro sistema de razonamiento sea lo suficientemente fuerte como para demostrarlo.
Hay varias maneras de rectificar este problema y hacer que nuestro sistema de razonamiento sea lo suficientemente fuerte., Una de las soluciones más antiguas es introducir un nuevo método de prueba, tradicionalmente llamado «reductio ad absurdum», que significa una reducción al absurdo. Este método también se llama a menudo una «prueba indirecta»o» derivación indirecta».
la idea es que asumimos la negación de nuestra conclusión, y luego mostramos que resulta una contradicción. Una contradicción se muestra cuando probamos alguna oración Ψ, y su negación Ψ. Puede ser cualquier frase. El punto es que, dado el principio de la bivalencia, debemos haber probado algo falso. Porque si Ψ es verdadero, entonces Ψ es falso; y si Ψ es verdadero, entonces Ψ es falso., No necesitamos saber cuál es falso (Ψ O Ψ); es suficiente saber que uno de ellos debe ser.
recuerde que hemos construido nuestro sistema lógico para que no pueda producir una falsedad a partir de declaraciones verdaderas. La fuente de la falsedad que producimos en la derivación indirecta debe, por lo tanto, ser alguna falsedad que agregamos a nuestro argumento. Y lo que añadimos a nuestro argumento es la negación de la conclusión. Por lo tanto, la conclusión debe ser verdadera.,
La forma del argumento es este:

Tradicionalmente, la asunción, de forma indirecta, la derivación también se ha llamado comúnmente «la asunción por reductio».
como ejemplo concreto, podemos probar nuestro caso desconcertante.

Nos supone la negación de la conclusión, y en la línea 4. La conclusión que creíamos correcta era P, y la negación de esto es P. en la línea 7, probamos R., Técnicamente, hemos terminado en ese punto, pero nos gustaría ser amables con cualquiera que intente entender nuestra prueba, por lo que repetimos la línea 3 para que las oraciones R y R estén lado a lado, y es muy fácil ver que algo ha ido mal. Es decir, si hemos probado tanto R Como R, entonces hemos probado algo falso.
nuestro razonamiento ahora es así. ¿Qué salió mal? La línea 8 es un uso correcto de la repetición; la línea 7 proviene de un uso correcto del modus tollendo ponens; la línea 6 de un uso correcto del modus ponens; la línea 5 de un uso correcto de la doble negación., Por lo tanto, no cometimos un error en nuestro razonamiento. Usamos las líneas 1, 2 y 3, pero esas son premisas que acordamos asumir que son correctas. Esto deja la Línea 4. Esa debe ser la fuente de mi contradicción. Debe ser falso. Si la Línea 4 es falsa, entonces P es verdadera.
algunas personas consideran que las pruebas indirectas son menos fuertes que las pruebas directas. Hay muchas y complejas razones para ello. Pero, para nuestra lógica proposicional, ninguna de estas razones se aplica. Esto se debe a que es posible probar que nuestra lógica proposicional es consistente., Esto significa que es posible probar que nuestra lógica proposicional no puede probar una falsedad a menos que uno primero introduzca una falsedad en el sistema. (Generalmente no es posible probar que los sistemas lógicos o matemáticos más poderosos y avanzados son consistentes, desde dentro de esos sistemas; por ejemplo, uno no puede probar en aritmética que la aritmética es consistente.) Dado que podemos estar seguros de la consistencia de la lógica proposicional, podemos estar seguros de que en nuestra lógica proposicional una prueba indirecta es una buena forma de razonamiento., Sabemos que si probamos una falsedad, debemos haber puesto una falsedad; y si confiamos en todas las otras suposiciones (es decir, las premisas) de nuestra prueba, excepto en la suposición de derivación indirecta, entonces podemos estar seguros de que esta suposición de derivación indirecta debe ser la fuente de la falsedad.
Se requiere una nota sobre la terminología aquí. La palabra «contradicción» se usa ambiguamente en la mayoría de las discusiones lógicas. Puede significar una situación como la que vemos arriba, donde se afirman dos oraciones, y estas oraciones no pueden ser verdaderas., O puede significar una sola oración que no puede ser verdad. Un ejemplo de tal oración es (P^P)., La tabla de verdad de esta frase es:
| P | P | (P ^ P) |
|---|---|---|
| T | F | C |
| F | T | F |
por Lo tanto, este tipo de oración nunca puede ser verdad, sea cual sea el significado de P.,
para evitar ambigüedades, en este texto, siempre llamaremos a una sola oración que no puede ser verdadera una «oración contradictoria». Por lo tanto, (P^P) es una oración contradictoria. Las situaciones en las que se afirman dos frases que no pueden ser verdaderas se denominarán «contradicción».
8.3 nuestro ejemplo, y otros ejemplos
podemos reconstruir una versión del argumento de Galileo ahora. Usaremos la siguiente clave.
P: hay infinitos reales (incluyendo los números naturales y los números cuadrados).,
Q: hay una correspondencia uno-a-uno entre los números naturales y los números cuadrados.
R: El tamaño del conjunto de los números naturales y el tamaño del conjunto de los números cuadrados son los mismos.
S: Todos los números cuadrados son números naturales.
T: algunos de los números naturales no son números cuadrados.
U: hay más números naturales que números cuadrados.,
Con esta clave, el argumento será traducida:
(P→Q)
(Q→R)
(P→(S^T))
((S^T)→U)
(U→R)
P
Y podemos probar que esto es un argumento válido mediante el uso indirecto de la derivación:

En la línea 6, asumimos que P porque Galileo creyó que P y objetivo de demostrar que el P. es decir, él cree que no existen infinitos, y tan asumido que era falso creer que no es el caso que no existen infinitos. Esta falsedad conducirá a otras falsedades, exponiéndose a sí misma.,
para aquellos que están interesados: Galileo concluyó que no hay infinitos reales, pero hay infinitos potenciales. Por lo tanto, razonó, no es el caso de que todos los números naturales existan (en algún sentido de «existir»), pero es cierto que se podría contar los números naturales para siempre. Muchos filósofos antes y después de Galileo sostuvieron este punto de vista; es similar a un punto de vista sostenido por Aristóteles, quien fue un importante lógico y filósofo que escribió casi dos mil años antes de Galileo.,
tenga en cuenta que en un argumento como este, podría razonar que no la suposición de derivación indirecta, sino más bien una de las premisas era la fuente de la contradicción. Hoy en día, la mayoría de los matemáticos creen esto sobre el argumento de Galileo. Un lógico y matemático llamado Georg Cantor (1845-1918), el inventor de la teoría de conjuntos, argumentó que los conjuntos infinitos pueden tener subconjuntos propios del mismo tamaño., Es decir, Cantor negó la premisa 4 anterior: a pesar de que todos los números cuadrados son números naturales, y no todos los números naturales son números cuadrados, no es el caso de que estos dos conjuntos sean de diferente tamaño. Cantor aceptó sin embargo la premisa 2 anterior, y, por lo tanto, creía que el tamaño del conjunto de números naturales y el tamaño del conjunto de números cuadrados es el mismo. Hoy en día, utilizando el razonamiento de Cantor, matemáticos y lógicos estudian el infinito, y han desarrollado un gran cuerpo de conocimiento sobre la naturaleza del infinito. Si esto le interesa, consulte la sección 17.5.,
consideremos otro ejemplo para ilustrar la derivación indirecta. Un conjunto muy útil de teoremas son hoy llamados «teoremas de De Morgan», por el lógico Augustus De Morgan (1806-1871). No podemos declararlos completamente hasta el Capítulo 9, pero podemos declarar su equivalente en inglés: DeMorgan observó que (PvQ) y (P^Q) son equivalentes, y también que (P^Q) y (PvQ) son equivalentes. Dado esto, debería ser un teorema de nuestro lenguaje que ((PvQ)→(P^Q)). Probemos esto.
toda la fórmula es condicional, por lo que usaremos una derivación condicional., Nuestra prueba debe comenzar:
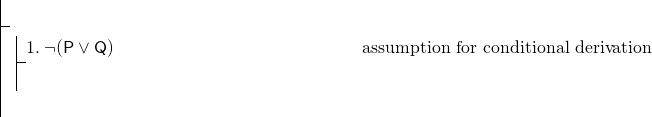
para completar la derivación condicional, debemos probar (P^Q). Esta es una conjunción, y nuestra regla para mostrar conjunciones es adjunción. Dado que usar esta regla podría ser nuestra mejor manera de mostrar (P^Q), podemos apuntar a mostrar P y luego mostrar Q, y luego realizar adjunción. Pero, obviamente, tenemos muy poco con qué trabajar – solo la línea 1, que es una negación. En tal caso, es típicamente sabio intentar una prueba indirecta. Comience con una prueba indirecta de P.,

ahora Tenemos que encontrar una contradicción, contradicción alguna. Pero ya hay una obvia. La línea 1 dice que ni P ni Q son verdaderas. Pero la línea 3 dice que P es verdadera. Debemos explicitar esta contradicción encontrando una fórmula y negándola. Podemos hacer esto usando suma.

Para completar la prueba, vamos a utilizar esta estrategia.

probaremos los teoremas de De Morgan como problemas para el Capítulo 9.,
Aquí hay una regla general para hacer pruebas: al probar un condicional, siempre haga derivación condicional; de lo contrario, intente derivación directa; si falla, entonces, intente derivación indirecta.
8.4 problemas
- Complete las siguientes pruebas. Cada uno requerirá una derivación indirecta. Los dos últimos son desafiantes.
- probar los siguientes son teoremas.
- (P^P).
- ((P→P)^(P→P)).
- (P→(P^Q)).
- ((P^Q)→(P→Q)).
- en inglés coloquial normal, escriba su propio argumento válido con al menos dos premisas., Su argumento debe ser solo un párrafo (no una lista ordenada de oraciones o cualquier otra cosa que parezca lógica formal). Tradúzcalo en lógica proposicional y demuestre que es válido usando una derivación indirecta.
esta traducción del título del libro de Galileo se ha convertido en la más común, aunque una más literal habría sido discursos matemáticos y demostraciones. Las traducciones del libro incluyen Drake (1974).