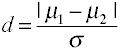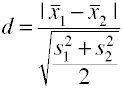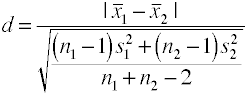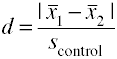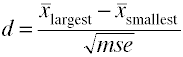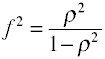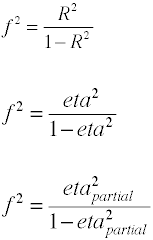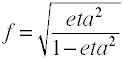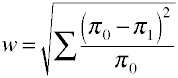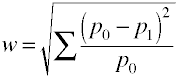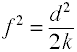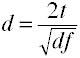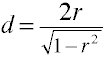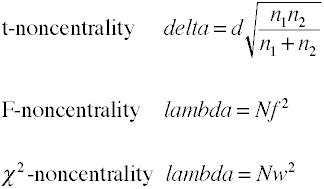une utilisation de la taille de l’effet est un indice normalisé indépendant de la taille de l’échantillon et quantifiant l’ampleur de la différence entre les populations ou la relation entre les variables explicatives et les variables de réponse. Une autre utilisation de la taille de l’effet est son utilisation dans l’effectuationanalyse de puissance.
taille de l’effet pour la différence de moyennes
La Taille de l’effet pour les différences de moyennes est donnée par le d de Cohen est défini en termes de moyennes de population (µs) et d’une éviation standard de population (σ), comme indiqué ci-dessous.,
Il existe plusieurs façons différentes d’estimer σ à partir de données d’échantillon qui conduisent à plusieurs variantes au sein de la famille D de Cohen.
en utilisant l’écart-type carré moyen
en utilisant l’écart-type groupé (g de Hedges)
Cette version du D de Cohen utilise écart type groupé et est également connu sous le nom de Hedges’ G.,
Vous pouvez facilement obtenir cette valeur à partir d’une analyse de variance (anova programme en prenant la racine carrée de la meansquare erreur qui est également connu comme la racine de l’erreur quadratique moyenne.
utilisation de L’écart type du groupe témoin (Glass’ Δ)
Une autre version du D de Cohen utilisant l’écart type du groupe témoin est également connue sous le nom de Glass’ Δ.,
Plus de deux groupes
Quand il y a plus de deux groupes d’utiliser la différence entre la plus grande et la smallestmeans divisé par la racine carrée de l’erreur quadratique moyenne.
la taille de l’Effet pour les F-ratios dans l’analyse de régression
De la régression MCO de la mesure des effets de taille est F qui est définie par Cohen comme suit.,
encore une Fois, il ya plusieurs façons dans lequel la taille de l’effet peut être calculé à partir des données de l’échantillon. Notece η2 est un autre nom pour R2.
la taille de l’Effet pour les F-ratios de l’analyse de la variance
La taille de l’effet utilisé dans l’analyse de la variance est définie par le rapport de la population standarddeviations.,
Bien que Cohen f est défini comme ci-dessus, il est généralement computedby en prenant la racine carrée de f2.
taille de L’effet pour χ2 à partir des tables de contingence
encore une fois, nous commençons par la formule de définition en termes de valeurs de population.La taille de l’effet w est la racine carrée de la statistique standardisée du chi carré.,
Et voici comment w est calculé à l’aide des données de l’échantillon.
Voici un tableau de valeurs suggérées pour basse, moyenne et haute des effets (Cohen, 1988). Ces valeurs ne doivent pas être considérées comme absolues et doivent être interprétées dans le contexte de votre programme de recherche. Les valeurs pour les grands effets sont souvent dépassées dans la pratique avec des valeurs de Cohen d supérieures à 1.0 pas rare.,Cependant, l’utilisation de très grandes tailles d’effets dans l’analyse prospective de la puissance n’est probablement pas une bonne idée, car elle pourrait conduire à des études sous-alimentées.,les formules
où k = nombre de groupes
Convertir en t, à d pour les deux groupes indépendants
Convertir les r de d pour les deux groupes indépendants
Noncentrality estimations
Analyse de la puissance à l’aide de méthodes analytiques nécessitent une estimation de noncentrality qui est basicallythe la taille de l’effet multiplié par la taille de l’échantillon facteur., Voici quelques formules pour estimer la non-centralité.
Exemple de la puissance d’analyse
Voici un exemple qui rassemble la taille de l’effet et noncentrality dans une analyse de puissance.
considérons une analyse unidirectionnelle de la variance avec trois groupes (k = 3). Si nous nous attendons à ce que andeta2 soit égal .,12 dans lequel cas la taille de l’effet est
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
Avec la prévision d’un échantillon de 60 l’estimation de noncentrality est
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
Le numérateur de degrés de liberté est k-1 = 3-1 = 2), alors que le dénominateur df est N-k = 60-3 = 57.La valeur critique de F avec 2 et 57 degrés de liberté est de 3,16. Ce qui se traduit par une puissance de
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
ainsi, un N de 60 et une taille d’effet de .369 donne une puissance projetée d’environ .7.
Nous pouvons améliorer la puissance de .7 en utilisant une taille d’échantillon projetée de 75 au lieu de 60., Avec le même effet de la taille de.369, nous obtenons une nouvelle estimation de non-centralité de
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
les degrés de liberté du numérateur restent les mêmes tandis que le dénominateur df est maintenant égal à N-k = 75-3 = 72.La valeur critique de F avec 2 et 72 degrés de liberté de 3.12. Cette fois, la puissance est
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
ce qui est dans les limites de recherche acceptables.
veuillez noter que différents paquets de statistiques utilisent des noms différents et un ordre d’arguments différent dans la fonction que nous avons appelée noncentralFtail. Vous aurez besoin de lire la documentation quivient avec votre logiciel.,
Becker, L. Psychologie 590 notes de cours. Consulté le 19 Juin 2009 <http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen, J. 1988. Analyse de puissance statistique pour les sciences du comportement. Hillsdale, New Jersey:Lawrence Erlbaum Associates