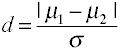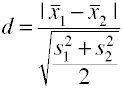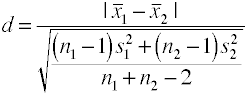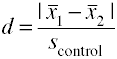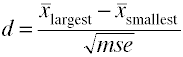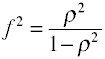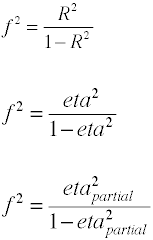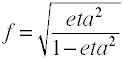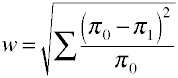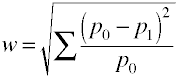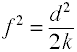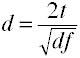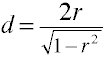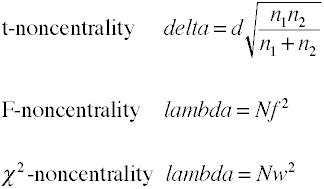Yksi käyttää vaikutus-koko on standardoitu indeksi, joka on riippumaton otoksen koosta ja määrällisesti suuruus ero väestön tai suhdetta selittävä ja vastemuuttujia. Toinen vaikutuskoon käyttö on sen käyttö tehoanalyysissä.
Vaikutus koko ero tarkoittaa,
Vaikutus koko eroja tarkoittaa, annetaan byCohen d on määritelty väkiluvultaan tarkoittaa (µs) ja väestön standarddeviation (σ), kuten alla.,
On olemassa useita eri tapoja että joku voisi arvioida, σ otostiedoille whichleads useita variantteja kuluessa Cohenin d perhe.
Käyttää neliöllinen keskiarvo keskihajonta
Käyttäen yhdistettyjä keskihajonta (Hedges’ g)
Tämä versio Cohenin d käyttää yhdistetty keskihajonta ja on tunnetaan myös nimellä Hedges’ g.,
Voit helposti saada tämän arvon anova program ottamalla neliöjuuri meansquare virhe, joka on tunnetaan myös nimellä root mean square error.
Käyttämällä kontrolliryhmä keskihajonta (Lasi’ Δ)
Toinen versio Cohenin d käyttää keskihajonta vertailuryhmä on myös tunnettu asGlass’ Δ.,
Lisää sitten kaksi ryhmää
Kun on enemmän sitten kaksi ryhmää käyttää ero suurimman ja smallestmeans, jaettuna, neliö root mean square error.
Vaikutus koko F-suhde regressioanalyysi
Varten OLS regressio toimenpiteen vaikutuksia koko on F, joka on määritelty Cohen seuraavasti.,
jälleen Kerran on olemassa useita tapoja, joilla vaikutus koko voidaan laskea näytteen tiedot. Noteettä η2 on toinen nimi R2.
Vaikutus koko F-suhde varianssianalyysi
vaikutus koko käytetty varianssianalyysi on määritelty suhteessa väestön standarddeviations.,
Vaikka Cohenin f on määritelty kuten edellä, se on yleensä computedby ottamalla neliöjuuri f2.
Vaikutus koko χ2 alkaen valmiussuunnitelma taulukot
jälleen Kerran aloitetaan vaativissa kaava kannalta väestön arvoja.Efektikoko w on standardoidun chi-neliötilaston neliöjuuri.,
Ja tässä on se, miten w on laskettu käyttämällä näytteen tiedot.
Tässä on taulukko ehdotti arvoja low, medium ja suuri vaikutus (Cohen, 1988). Näitä arvoja ei pidä pitää ehdottomina ja niitä tulisi tulkita tutkimusohjelmasi puitteissa. Laajempien vaikutusten arvot ylittyvät usein käytännössä, ja Cohenin d-arvo on yli 1,0, ei ole harvinainen.,Kuitenkin, käyttäen erittäin suuri vaikutus koot tulevaisuuden voima-analyysi on luultavasti ole hyvä idea, sillä se voisi johtaa alle powered tutkimukset.,kaavat
missä k = ryhmien määrä
Muunna t d kaksi riippumattomien ryhmien
Muuntaa r-k kaksi riippumattomien ryhmien
Noncentrality arvioiden
Vallan analyysi käyttäen analytic menetelmät vaativat arvio noncentrality joka on basicallythe vaikutus koko kerrottuna näytteen koko tekijä., Seuraavassa on joitakin kaavoja, joilla voidaan arvioida keskittymättömyyttä.
Esimerkki voima-analyysi
Tässä on esimerkki, joka tuo yhteen vaikutus koko ja noncentrality teho-analyysi.
harkitse varianssin yksisuuntaista analyysiä kolmen ryhmän kanssa (k = 3). Jos odotamme andeta2: n olevan yhtä suuri .,12 joka tapauksessa vaikutus koko on
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
ennustetaan otoskoko 60 arvio noncentrality on
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
osoittajan vapausasteet on k-1 = 3-1 = 2, kun nimittäjä df on N-k = 60-3 = 57.F: n kriittinen arvo 2 ja 57 asteen vapaudessa on 3,16. Joka johtaa voima
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
näin ollen N-60 ja vaikutus koko .369 tuottaa ennustetun voiman noin .7.
voimme parantaa tehoa.7 käyttämällä ennustettua näytteen kokoa 75 eikä 60., Sama vaikutus koko.369, me saada uusi noncentrality arvio
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
osoittajan vapausasteet pysyvät samana, kun taas nimittäjä df nyt tasa-N-k = 75-3 = 72.F: n kriittinen arvo 2 ja 72 asteen vapaudessa 3,12. Tällä kertaa virta on
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
joka on hyväksyttävissä tutkimuksen rajoja.
huomaa, että eri stat paketteja käyttää eri nimet ja eri järjestyksessä argumentit inthe-toiminto, joka meillä on soittaa noncentralFtail. Sinun täytyy lukea dokumentaatio, joka vastaa ohjelmiston kanssa.,
Becker, L. Psychology 590 course notes. Katsotuimmat 19 Jun 2009 <http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen, J. 1988. Tilastollinen tehoanalyysi käyttäytymistieteille. Hillsdale, New Jersey:Lawrence Erlbaum Associates