regressiomalliin Selviytymisen Tiedot
olen aiemmin kirjoittanut siitä, miten laskea Kaplan–Meier-käyrä selviytymisen tiedot. Ei-parametrinen estimaattori, se tekee hyvää työtä antaa vilkaista selviytymisen käyrä datajoukolle. Se ei kuitenkaan anna sinun mallintaa kovariaattien vaikutusta selviytymiseen. Tässä artikkelissa keskitymme Cox Proportional Hazards-malliin, joka on yksi käytetyimmistä selviytymistietojen malleista.
mennään johonkin syvyyteen, miten arviot lasketaan., Tämä on arvokasta, koska näemme, että arviot riippuvat vain epäonnistumisten tilaamisesta eivätkä niiden todellisesta ajasta. Käsittelemme myös lyhyesti joitakin kiperiä kysymyksiä syy-seuraus-päättelystä, jotka ovat erityisiä selviytymisanalyysille.
yleensä ajattelemme eloonjäämistietoja alla olevan kaltaisten elossaolokäyrien suhteen.,
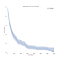
x-akselilla, meillä on aikaa päivää. Y-akselilla meillä on (estimaattori) prosenttiosuus (teknisesti, osuus) väestöstä, jotka ”hengissä” siihen aikaan. Säilyminen voi olla kuvaannollista tai kirjaimellista., Se voisi olla, onko ihmiset elävät tietyn iän, onko kone tekee se tietty määrä aikaa rikkomatta alas, tai se voisi olla, onko joku pysyy työttömänä tietyn ajan jälkeen menettää työpaikkansa.
ratkaisevaa on, että survival-analyysin komplikaatio on se, että joillakin tutkimushenkilöillä ei ole havaittu heidän ”kuolemaansa”. He saattavat olla vielä elossa, kone voi vielä toimia tai joku voi olla vielä tietojen keräämishetkellä työttömänä., Tällaisia havaintoja kutsutaan ”oikealta sensuroitu” ja tekemisissä sensuuri tarkoittaa, että selviytyminen analyysi edellyttää erilaisia tilastollisia työkaluja.
merkitsemme eloonjääneen funktiota s, ajan funktiona. Sen tuotos on niiden koehenkilöiden prosenttiosuus, jotka ovat säilyneet ajassa t. (taas se on teknisesti 0-1, mutta käytän näitä kahta sanaa vaihdellen). Yksinkertaisuuden vuoksi teemme teknisen oletuksen, että jos odotamme tarpeeksi kauan, kaikki aiheet ”kuolevat.”
indeksoimme koehenkilöt I: n tai j: n kaltaisella alaindeksillä., Epäonnistuminen kertaa koko väestöstä on merkitty vastaavat alaindeksi aika-muuttuja t.

Toinen hienous harkita, onko meidän hoitavan aikaa kuin diskreetti (viikko viikolta, sanoa) tai jatkuva. Filosofisesti, me vain koskaan mitata aikaa diskreetti välein (lähimpään toisen, sanoa)., Yleisesti tietomme kertovat vain, jos joku kuoli tiettynä vuonna tai jos kone epäonnistui tiettynä päivänä. Menen edestakaisin erillisten ja jatkuvien tapausten välillä, jotta näyttely olisi mahdollisimman selkeä.
Kun yritämme malli vaikutuksia muuttujien (esim. ikä, sukupuoli, rotu, koneen valmistaja) me yleensä olla kiinnostuneita ymmärtämään vaikutus kovariaatin Vaaran Tahtiin. Riskiprosentti on epäonnistumisen/kuoleman/valtion siirtymisen hetkellinen todennäköisyys tiettynä ajankohtana t, sillä edellytyksellä, että se on jo selvinnyt näin pitkään., Me merkitsemme sitä λ(t). Hoitoon aikaa kuin diskreetti:
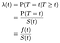
Missä f on yleinen todennäköisyys tiheys jättänyt ajankohtana t. Voimme yhtenäistää diskreetti ja jatkuva tapauksissa antamalla delta toimintoja todennäköisyys tiheys ”- toiminto”. Näin ollen tulos λ = f/S on sama jatkuvassa tapauksessa.
Let ’ s fix an example., Katsotaanpa yhteydessä kliinisen tutkimuksen, jossa lääke aluksi aiheuttaa taudin mennä remissioon. Voimme sanoa, että lääke ”ei” aihe, kun tauti alkaa edetä aiheesta. Lopuksi oletetaan, että koehenkilöiden tautitilat mitataan joka viikko. Sitten jos λ(3) = 0.1, se tarkoittaa, että siellä on 10% mahdollisuus, että annetaan aihe, jos ne ovat edelleen remissiossa ennen kuin viikko 3, tauti alkaa edetä tällä viikolla 3. Loput 90 prosenttia jäävät remissioon.,
seuraavaksi yleinen todennäköisyystiheysfunktio f on vain S: n derivaatta ajan suhteen. (Jälleen, jos aika on diskreetti, f on vain summa delta-toiminnot).,341fa8b2″>
Tämä tarkoittaa sitä, että jos tiedämme, Vaara-toiminto, voimme ratkaista tämän differentiaaliyhtälön S:
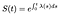
Jos aikaa on erillinen, kiinteä summa delta toimii vain, muuttuu summa vaarat kullakin diskreetti aika.,
Okay, joka tiivistää notaation ja peruskäsitteet, joita tarvitsemme. Siirrytään keskustelemaan malleista.
Ei-, Osittain-ja Täysin Parametrinen Malleja
Kuten aiemmin sanoin, olemme yleensä kiinnostuneita mallinnus Hazard Rate λ.
ei-parametrisessa mallissa ei tehdä oletuksia λ: n funktionaalisesta muodosta. Kaplan-Meier-käyrä on tässä tapauksessa suurin Todennäköisyysarvioija. Varjopuolena on, että tämän vuoksi kovariaattien vaikutuksia on vaikea mallintaa. Se on vähän kuin scatter-juonen avulla ymmärtäisi kovariaatin vaikutuksen., Ei välttämättä yhtä hyödyllinen kuin täysin parametrinen malli, kuten lineaarinen regressio.
täysin parametrisessa mallissa teemme oletuksen λ: n täsmälliselle funktionaaliselle muodolle. Keskustelu täysin parametrisista malleista on täysi artikkeli sinänsä, mutta siitä kannattaa käydä hyvin lyhyt keskustelu. Alla olevassa taulukossa on kolme yleisintä täysin parametrista mallia. Jokainen on yleistetty seuraava, menee 1-2-3 parametrit. Vaarafunktion funktionaalinen muoto esitetään keskimmäisessä sarakkeessa. Vaarafunktion logaritmi esitetään myös viimeisessä sarakkeessa., Kaikki parametrit (toimenpiteet, α, µ) oletetaan olevan positiivinen, paitsi että μ voisi olla 0-yleistynyt Weibull-jakauma (toisto Weibull-jakauma).

Tarkasteltaessa logaritmi osoittaa meille, että eksponentiaalinen malli olettaa, että vaaran toiminta on jatkuvaa. Weibull-malli olettaa, että on kasvava, jos α>1, vakio, jos α=1, ja vähentää, jos α<1., Yleistynyt Weibull-malli alkaa samalla tavalla kuin Weibull-malli (alussa ln S = 0). Sen jälkeen alkaa ylimääräinen termi μ.
näiden mallien ongelma on se, että ne tekevät vahvoja oletuksia tiedoista. Tietyissä yhteyksissä voi olla syytä uskoa, että nämä mallit sopivat hyvin yhteen. Mutta nämä ja useita muita vaihtoehtoja, on olemassa suuri riski, piirustus virheellisiä päätelmiä, koska misspecification malli.
tästä syystä Coxin suhteelliset vaarat, puoliparametrinen malli on niin suosittu., Vaarafunktion muodosta ei tehdä toiminnallisia oletuksia, vaan pelkästään kovariaattien vaikutuksista tehdään funktionaalisia oletuksia.,
Ja Coxin suhteellisen Vaaran Malli
Coxin suhteellisen Vaaran Malli on yleensä antanut kannalta aika t, kovariaatin vektori x, ja kerroin vektorin β kuin
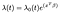
jos λₒ on mielivaltainen funktio aikaa, baseline hazard. X: n ja β: n pistetuote otetaan eksponentissa aivan kuten tavallisessa lineaarisessa regressiossa., Riippumatta arvoista kovariaatit, kaikilla koehenkilöillä on sama lähtötason vaara λ λ. Sen jälkeen tehdään muutoksia kovariaattien perusteella.
Tulkinta Tulokset
Oletetaan, että hetkellä, että meillä on sovittaa Coxin suhteellisen Vaaran malli meidän tiedot, joka koostui
- sarake täsmennetään aikaa kuhunkin aiheeseen
- sarake, jossa esitetään, ovatko aihe oli ”havaittu” (epäonnistuneen, tai, meidän ensisijainen esimerkiksi, on niiden taudin eteneminen). Arvo 1 tarkoittaa, että koehenkilöllä oli taudin etenemistä., Arvo 0 tarkoittaa, että viimeisellä havaintoajalla tauti ei ollut edennyt. Havainto sensuroitiin.
- kolumnit kovariaateille X.
sovituksen jälkeen saamme arvot β: lle. Oletetaan esimerkiksi yksinkertaisuuden vuoksi, että on olemassa yksi kovariaatti. Arvo β=0.1 tarkoittaa sitä, että lisäys kovariaatin, jonka määrä on 1 johtaa noin 10% suuri mahdollisuus taudin etenemistä milloin tahansa., Tarkka arvo on itse asiassa

pienet arvot β arvo β itsessään on melko hyvä likiarvo tarkan lisätä hazard. Suuremmille β-arvoille on laskettava tarkka määrä.
Toinen tapa ilmaista β=0.1 on, että, kun x kasvaa, vaara kasvaa nopeudella 10% vuodessa kasvu x 1. Suurempi 10.,52% syntyy (jatkuvasta) kompuroinnista, aivan kuten yhdistetyllä korolla.
myös β=0 tarkoittaa ei vaikutusta, ja β-negatiivinen tarkoittaa, että vaara on pienempi kovariaatin kasvaessa. Huomaa, että toisin kuin normaaleissa regressioissa, ei ole intercept-termiä. Sen sijaan sieppaus imeytyy lähtötason vaaraan λₒ, joka voidaan myös arvioida (KS.alla).
lopulta, olettaen, että olemme arvioineet lähtötilanteen vaaratoiminnon, voimme rakentaa eloonjääneen funktion.,
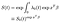
baseline-toiminto on potenssiin exp(xʹß) tekijä lähtöisin muuttujien. Eloonjääneen lähtötilanteen funktion tulkinnassa on noudatettava jonkin verran varovaisuutta, sillä se on suurin piirtein intercept-termin rooli säännöllisessä lineaarisessa regressiossa. Jos kovariaatit on keskitetty (keskiarvo 0), se edustaa selviytyjän funktiota ”keskimääräiselle” subjektille.,
Arvioidaan Coxin suhteellisen Vaaran Malli
Vuonna 1970, David Cox, Brittiläinen matemaatikko, ehdotettu tapa arvioida β ilman arvioivat baseline hazard λₒ. Myös lähtötason vaara voidaan arvioida jälkikäteen. Kuten edellä mainittiin, huomaamme, että on kyse Havaittujen epäonnistumisten tilaamisesta, ei itse ajoista.
ennen estimaattiin hyppäämistä kannattaa keskustella siteistä. Koska olemme yleensä vain tarkkailemalla tiedot diskreetti välein, on mahdollista, että kaksi epäonnistumisia voi tapahtua samaan aikaan., Esimerkiksi kaksi konetta saattaa pettää saman viikon aikana, ja nauhoitus tehdään vain viikoittain. Nämä siteet tekevät tilanteen analysoinnista melko monimutkaista lisäämättä paljon näkemystä. Näin ollen johdan arviot, jos ei ole siteitä.
muista, että tietomme koostuvat havainnoista eräistä lukuvirheistä diskreetin aikaan. Merkitköön r (t) populaatio ”riskiryhmässä” ajankohtana t. jos tutkimuksemme kohde on epäonnistunut (tauti on edennyt esimerkiksi) ennen aikaa t, he eivät ole ”vaarassa.,”Myös, jos tutkimuksemme kohde on sensuroinut havaintonsa aikana ennen t: tä, he eivät myöskään ole ”vaarassa.”
tavallista muoti, haluamme rakentaa uskottavuusfunktio (mikä on todennäköisyys, meillä olisi havaittu tiedot teimme, koska muuttujien ja kertoimien) ja sitten optimoida, että saada enintään-todennäköisyyden estimaattori.
jokaisen diskreetin ajan, jolloin havaitsimme subjektin j: n epäonnistumisen, sen todennäköisyys, Kun otetaan huomioon, että epäonnistuminen tapahtui, on alla. Summa otetaan kaikkien riskialttiiden aineiden haltuun ajankohtana j.,

Huomaa, että baseline hazard λₒ on pudonnut pois! Erittäin kätevää. Tästä syystä todennäköisyys, jonka rakennamme, on vain osittainen todennäköisyys. Huomaa myös, että ajat eivät näy lainkaan., Termi sovelletaan j riippuu vain siitä, mitä aiheita ovat vielä elossa, aika j, joka puolestaan riippuu vain järjestyksen, jossa tutkittavat ovat sensuroitu tai havaittu epäonnistua.
osittainen todennäköisyys on tietenkin vain tuotteen näiden ehtojen, yksi kutakin vika havaitsemme (n ehdot sensuroitu havaintoja).,
kirjautuminen osittainen todennäköistä on sitten,
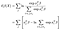
fit on tehty standardin numeerisia menetelmiä, esimerkiksi python paketti statsmodels ja varianssi-kovarianssi matriisin arviot annetaan (käänteinen) Fisher Tietoja Matriisi. Täällä ei ole mitään jännittävää.,
arvioitaessa lähtötilanteen eloonjääneen funktiota
nyt kun olemme arvioineet kertoimet, voimme arvioida eloonjääneen funktion. Tämä päätyy hyvin samanlaiseksi kuin Kaplan–Meier-käyrän arvioiminen.
edellytämme ehdot α indeksoitu minä. Tällä kertaa minä, lähtötilanteessa perhe käyrä vähenee murto-α eli osa aiheista on riski, että ette tällä kertaa en., Toisin sanoen
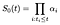
laske suurimman uskottavuuden estimaattori α, ajatellaan, todennäköisyys, osuus alkaen aihe, minä, joka ei tällä kertaa minä ja erikseen panosta niiltä, jotka ovat sensuroitu tällä kertaa minä.
aihe, joka epäonnistuu kerta, todennäköisyys on, koska todennäköisyys, että he ovat elossa tällä kertaa olen vähemmän todennäköisyys he ovat elossa seuraavan kerran, i+1. (Oletamme hetkellisesti, että ajat on tilattu).,
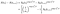
Jos sen sijaan ne ovat sensuroitu tällä kertaa minä, osuus on vain todennäköisyys, että he ovat elossa silloin, kun minä, eli että he eivät ole vielä kuollut., Tämä on vain
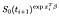
Siellä on ylimääräinen termi aiheita, jotka olivat havaittu (eli havaittu epäonnistua sijaan sensuroitu)., Kirjautuminen todennäköisesti tulee
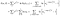
olen ollut vähän huolimaton noin pitää kirjaa päätepisteet (minä vs. i+1), mutta se kaikki toimi ulos.
on olemassa vain α-termejä tutkimushenkilöille, joiden havaitsimme epäonnistuneen., Erottaa osalta α-j ja olettaen, että ei ole siteitä, saamme osuus alkaen summa vasemmalla vain aiheita, elossa ajanhetkellä j, ja yksittäinen rahoitusosuus termi oikealla.,kars 0 tarkoittaa, että voimme saada suurimman uskottavuuden estimaatit α käyttämällä arvioita β kuin ratkaisu useita yhtälöitä, yksi kustakin aiheesta, joka oli havaittu epäonnistua:
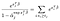
Laajennukset ja Varoitukset
Siellä on paljon enemmän sanottavaa Coxin suhteellisen Vaaran mallit, mutta yritän pitää asiat lyhyesti ja vain mainita muutamia asioita.,
esimerkiksi ajallisesti vaihtelevia regressoreita kannattaa harkita, ja tämä on mahdollista.
toinen tärkeä asia pitää mielessä on jätetty pois muuttuja harhaa. Standard lineaarisessa regressiossa poistetut muuttujat, jotka eivät liity regressoreihin, eivät ole suuri ongelma. Tämä ei pidä paikkaansa selviytymisanalyysissä. Oletetaan, että meillä on kaksi samankokoista ja otokseen valitut alaryhmät meidän tiedot kunkin jatkuva hazard rate, yksi on 0,1 ja toinen on 0.5. Aluksi näemme korkean riskiprosentin (keskiarvo, vain 0,3)., Ajan mittaan väestömäärä, jolla on korkea riskitaso, poistuu väestöstä, ja havaitsemme vaaran vähenevän 0,1: een. Jos jätämme pois muuttujan, joka edustaa näitä kahta väestöä, lähtötilanteen riskiprosenttimme on sekaisin.