8.1 historiallinen esimerkki
kirjassaan, Kaksi Uutta Tieteet, Galileo-Galilea (1564-1642) antaa useita argumentteja tarkoitus osoittaa, että ei voi olla sellaista asiaa kuin todellinen äärettömiä tai todellinen infinitesimals. Yksi hänen perusteluistaan voidaan rekonstruoida seuraavalla tavalla. Galileo ehdottaa, että otamme oletuksesta, että on olemassa todellinen infinity luonnolliset luvut (luonnolliset luvut ovat positiivisia kokonaislukuja alkaen 1):
{1, 2, 3, 4, 5, 6, 7, ….,}
hän ehdottaa myös, että otamme lähtökohdaksi sen, että luonnollisten lukujen neliöiden todellinen äärettömyys on olemassa.
{1, 4, 9, 16, 25, 36, 49, ….}
nyt, Galileo syistä, huomaa, että nämä kaksi ryhmää (tänään kutsuisimme niitä ”sarjoiksi”) ovat samankokoisia. Voimme nähdä tämän, koska voimme nähdä, että näiden kahden ryhmän välillä käydään kahdenkeskistä kirjeenvaihtoa.,
| {1, | 2, | 3, | 4, | 5, | 6, | 7, ….,div> | |
| {1, | 4, | 9, | 16, | 25, | 36, | 49, …} |
Jos voimme liittää jokainen luonnollinen luku, jossa on yksi ja vain yksi neliö numero, ja jos voimme yhdistää jokaisen neliön numero yksi ja vain yksi luonnollinen luku, niin nämä sarjat on oltava sama koko.,
Mutta odota hetki, Galileo sanoo. Luonnollisia lukuja on selvästi paljon enemmän kuin neliönumeroita. Että on, jokainen neliö numero on luettelossa luonnolliset luvut, mutta monet luonnolliset luvut eivät ole luettelossa neliön numerot. Seuraavat numerot ovat kaikki luonnollisten lukujen luettelossa, mutta eivät neliönumeroiden luettelossa.
{2, 3, 5, 6, 7, 8, 10, ….,}
Niin, Galileo syistä, jos on paljon numeroita ryhmä luonnolliset luvut, jotka eivät ole ryhmän neliön numerot, ja jos ei ole numeroita ryhmän neliön numerot, jotka eivät ole naturals numerot, niin luonnolliset luvut on suurempi kuin neliön numerot. Ja jos ryhmä luonnolliset luvut on suurempi kuin ryhmä, neliön numerot, niin luonnolliset luvut ja neliön numerot eivät ole samankokoisia.,
– Meillä on kaksi päätelmää: joukko luonnolliset luvut ja joukko neliön numerot ovat samankokoisia, ja joukko luonnolliset luvut ja joukko neliön numerot eivät ole samankokoisia. Se on ristiriitaista.
Galileo perustelee ristiriitaa sillä, että oletimme, että on olemassa todellisia äärettömyyksiä. Hän päättelee näin ollen, että varsinaisia äärettömyyksiä ei ole.
8.2 epäsuorat todisteet
logiikkamme ei ole vielä tarpeeksi vahva todistamaan joitakin päteviä argumentteja. Tarkastellaanpa esimerkiksi seuraavaa väitettä.,
(P→(QvR))
Q
R
P
Tämä argumentti näyttää voimassa. Ensimmäinen lähtökohta tiedämme: jos P olisi totta, niin niin olisi (Q v R) totta. Mutta sitten joko Q tai R tai molemmat olisivat totta. Ja toisen ja kolmannen tilan me tiedämme: Q on väärä ja R on väärä. Joten se ei voi olla, että (Q v R) on totta, ja niin se voi olla, että P on totta.
argumentin voi tarkistaa totuustaulukosta. Pöytämme on monimutkainen, koska yksi lähtökohdistamme on monimutkainen.,
In any kind of situation in which all the premises are true, the conclusion is true., Toisin sanoen: tilat ovat kaikki totta vasta viimeisellä rivillä. Tuolle riville johtopäätös on myös totta. Tämä on siis Pätevä perustelu.
mutta ota minuutti ja yritä todistaa tämä väite. Aloitamme

Ja nyt olemme lakanneet. Emme voi soveltaa mitään sääntöjämme. Tässä on pätevä argumentti, että emme ole tehneet järkeilyjärjestelmästämme tarpeeksi vahvaa todistaaksemme.
On olemassa useita tapoja korjata tämä ongelma ja tehdä päättely järjestelmä tarpeeksi vahva., Yksi vanhimmista ratkaisuja on ottaa käyttöön uusi proof menetelmä, perinteisesti kutsutaan ”äärimmäisenä”, joka tarkoittaa vähentää järjettömyyttä. Tätä menetelmää kutsutaan usein myös ”epäsuoraksi todisteeksi”tai” epäsuoraksi johdannaiseksi”.
ajatuksena on, että oletamme johtopäätöksemme kieltävän ja osoitamme sitten, että tuloksena on ristiriita. Ristiriita näkyy, kun todistamme jonkin lauseen Ψ, ja sen negaatio Ψ. Tämä voi olla mikä tahansa lause. Kyse on siitä, että kun otetaan huomioon bivalenssiperiaate, meidän on täytynyt todistaa jotain väärää. Esimerkiksi, jos Ψ on totta, niin Ψ on väärä; ja jos Ψ on totta, niin Ψ on väärä., Meidän ei tarvitse tietää, mikä on väärä (Ψ Tai Ψ); riittää, että tiedämme, että yksi niistä on.
muista, että olemme rakentaneet loogisen järjestelmämme niin, ettei se voi tuottaa valhetta todellisista lausunnoista. Sen valheen lähteen, jonka tuotamme epäsuorassa johdantokappaleessa, täytyy siksi olla jokin valhe, jonka lisäsimme väitteeseemme. Lisäsimme väitteeseemme johtopäätöksen kieltämisen. Johtopäätöksen täytyy siis olla totta.,
muoto argumentti on kuin tämä:

Perinteisesti oletus epäsuora johtaminen on myös yleisesti kutsutaan ”oletus väheni”.
konkreettisena esimerkkinä voimme todistaa hämmentävän tapauksemme.

oletimme kieltäminen meidän johtopäätös linjalla 4. Johtopäätös, jonka uskoimme olevan oikea, oli P, ja tämän kieltäminen on P. rivillä 7, todistimme R., Teknisesti olemme valmiita tässä vaiheessa, mutta haluamme olla ystävällinen kaikille, yrittää ymmärtää meidän todisteita, joten emme toista linja 3 niin, että lauseet R ja R ovat vierekkäin, ja se on erittäin helppo nähdä, että jotain on mennyt pieleen. Toisin sanoen, jos olemme todistaneet sekä R että R, olemme todistaneet jotain väärää.
meidän päättelymme menee nyt näin. Mikä meni vikaan? Linja 8 on oikea käyttö toistoa; linja 7 tulee oikea käyttö modus tollendo ponens, lambda; line 6 oikea käyttö modus ponens, lambda; linja 5 oikea käyttö kaksinkertainen negaatio., Emme siis tehneet virhettä perusteluissamme. Käytimme linjoja 1, 2 ja 3, mutta ne ovat tiloja, joiden olemme sopineet olevan oikein. Tämä jättää linjan 4. Sen täytyy olla ristiriitani lähde. Sen täytyy olla valhetta. Jos linja 4 on väärä, niin P on totta.
jotkut pitävät epäsuoria vedoksia vähemmän vahvoina kuin suoria vedoksia. Syitä tähän on monia ja monimutkaisia. Mutta ehdotuslogiikastamme mikään näistä syistä ei päde. Tämä johtuu siitä, että on mahdollista todistaa, että propositiologiikkamme on johdonmukainen., Tämä tarkoittaa, että se on mahdollista todistaa, että meidän lauselogiikka logiikka ei voi todistaa valhetta, ellei ensin esittelee valheeseen järjestelmään. (Se ei yleensä ole mahdollista todistaa, että enemmän voimakas ja kehittynyt looginen tai matemaattinen järjestelmät ovat yhdenmukaisia keskenään, sisältä näihin järjestelmiin; esimerkiksi yksi voi todistaa aritmeettinen, että aritmeettinen on johdonmukainen.) Koska voimme olla varmoja propositiologiikan johdonmukaisuudesta, voimme olla varmoja siitä, että propositiologiikassamme epäsuora todiste on hyvä päättelyn muoto., Me tiedämme, että jos me todistaa valhetta, meidän täytyy laittaa valhetta; ja jos olemme varmoja siitä, että kaikki muut oletukset (joka on, tiloista) meidän todiste paitsi oletus epäsuora johtaminen, voimme olla varmoja, että tämä oletus epäsuora johtaminen on lähde valheen.
tässä on maininta terminologiasta. Sanaa ”ristiriita” käytetään epäselvästi useimmissa logiikkakeskusteluissa. Se voi tarkoittaa tilannetta, kuten näemme edellä, jossa lauseita on kaksi, eivätkä nämä lauseet voi molemmat olla totta., Tai se voi tarkoittaa yhtä lausetta, joka ei voi olla totta. Esimerkki tällaisesta lauseesta on (P^P)., Totuus taulukossa tämä lause on:
| P | P | (P ^ P) |
|---|---|---|
| T | F | F |
| F | T | F |
Näin ollen, tällainen lause ei voi koskaan olla totta, riippumatta merkitys P.,
epäselvyyksien välttämiseksi tässä tekstissä, me aina soittaa yhden lauseen, että ei voi olla totta ”ristiriitainen lause”. Niinpä (P^P) on ristiriitainen lause. Tilanteita, joissa väitetään kahta lausetta, jotka eivät voi molemmat olla totta, kutsutaan ”ristiriidaksi”.
8.3 Meidän esimerkki, ja muita esimerkkejä
Voimme rekonstruoida versio Galileo-väite nyt. Käytämme seuraavaa avainta.
S: On olemassa todellinen äärettömiä (mukaan lukien luonnolliset luvut ja square numbers).,
Q: luonnollisten lukujen ja neliönumeroiden välillä on yksi yhteen-kirjeenvaihto.
T: koko joukko luonnolliset luvut ja koko joukko neliön numerot ovat samat.
S: kaikki neliönumerot ovat luonnollisia lukuja.
T: osa luonnollisista luvuista ei ole neliönumeroita.
U: luonnollisia lukuja on enemmän kuin neliönumeroita.,
tämä keskeinen väite on käännetty:
(P→Q)
(Q→R)
(P→(T^T))
((T^T)→U)
(U→T)
P
Ja voimme todistaa, että tämä on voimassa oleva argumentti käyttämällä epäsuoraa johtamista:

On line 6, oletimme, että P, koska Galileo uskoi, että P ja pyritään osoittamaan, että P., Että on, hän uskoi, että on olemassa ei varsinainen äärettömyydet, ja niin olettaa, että se oli vääriä uskoa, että se ei ole tapauksessa että siellä ei ole varsinaisia äärettömiä. Tämä valhe johtaa muihin valheisiin paljastaen itsensä.,
kiinnostuneille: Galileo päätteli, että varsinaisia infinititejä ei ole, mutta potentiaalisia infinititejä on. Näin ollen hän päätteli, ettei ole niin, että kaikki luonnolliset luvut olisivat olemassa (jossain merkityksessä ”olemassa”), mutta on totta, että luonnollisia lukuja voisi laskea ikuisesti. Monet filosofit ennen ja jälkeen Galileo piti tätä näkemystä; se on samanlainen näkemys oli Aristoteles, joka oli tärkeä loogikko ja filosofi kirjoittaa lähes kaksi tuhatta vuotta, ennen kuin Galileo.,
Huomaa, että argumentti kuin tämä, voit syystä, että ei oletus epäsuoraa johtamista, vaan pikemminkin yksi tiloista oli lähde ristiriita. Nykyään useimmat matemaatikot uskovat tämän Galilein väitteestä. Joukko-opin keksijä ja matemaatikko Georg Cantor (1845-1918) esitti, että äärettömillä joukoilla voi olla samankokoisia osajoukkoja., Että on, Kanttori evätään lähtökohta 4 edellä: vaikka kaikki square numerot ovat luonnolliset luvut, ja kaikki luonnolliset luvut ovat neliön numerot, kyse ei ole siitä, että nämä kaksi sarjaa ovat eri kokoisia. Kanttori hyväksyi kuitenkin lähtökohta 2 edellä, ja siten, uskotaan, että koko joukko luonnolliset luvut ja koko joukko neliön numerot on sama. Nykyään Cantorin päättelyn avulla matemaatikot ja loogikot tutkivat äärettömyyttä ja ovat kehittäneet suuren tietoryhmän äärettömyyden luonteesta. Jos tämä kiinnostaa sinua, katso kohta 17.5.,
Tarkastellaanpa toista esimerkkiä epäsuoran derivoinnin havainnollistamiseksi. Erittäin hyödyllinen joukko teoreemojen kutsutaan tänään” De Morganin teoreemojen ” jälkeen loogikko Augustus De Morgan (1806-1871). Emme voi valtion nämä täysin vasta luvussa 9, mutta voimme todeta niiden vastaavan englanti: DeMorgan havaittu, että (PvQ) ja (P^Q) ovat vastaavia, ja myös, että (P^Q) ja (PvQ) ovat vastaavia. Koska tämä, sen pitäisi olla lause meidän kieli, että ((PvQ)→(P^Q)). Todistetaan tämä.
koko kaava on ehdollinen, joten käytämme ehdollinen johtaminen., Meidän todiste on siten alkaa:
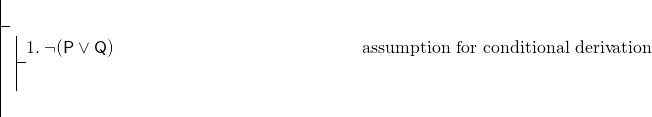
täydellinen ehdollinen johtaminen, meidän täytyy todistaa (P^Q). Tämä on Konjunktio, ja meidän sääntö osoittaa Konjunktio on adjunktio. Koska tämän säännön käyttö voi olla paras tapa näyttää (P^Q), voimme pyrkiä näyttämään P ja sitten näyttää Q, ja sitten suorittaa adjunction. Mutta, meillä on selvästi hyvin vähän työtä—vain linja 1, joka on negaatio. Tällaisessa tapauksessa on tyypillisesti viisasta yrittää epäsuoraa todistetta. Aloita epäsuoralla todisteella P.,

– Meidän täytyy nyt löytää ristiriita—mitään ristiriitaa. Mutta yksi on jo ilmeinen. Linja 1 sanoo, ettei P tai Q pidä paikkaansa. Mutta linja 3 sanoo, että P on totta. Meidän on tehtävä tämä ristiriita selväksi löytämällä kaava ja sen kieltäminen. Voimme tehdä tämän lisäämällä.

täydellinen todiste, käytämme tätä strategiaa uudelleen.

Meidän tulee todistaa, De Morganin lauseet kuin ongelmia, luku 9.,
Tässä on yleinen nyrkkisääntö, että teet vedoksia: Kun todistaa ehdollinen, aina ehdollinen johtaminen; muuten, kokeile suora johtaminen; jos se epäonnistuu, sitten kokeilla epäsuoraa johtamista.
8.4 Ongelmia
- Täydennä seuraavat todisteet. Jokainen edellyttää epäsuoraa derivointia. Kaksi viimeistä ovat haastavia.
- Todista seuraavat ovat teoreemoja.
- (P^P).
- ((P→P)^(P→P)).
- (P→(P^Q)).
- ((P^Q)→(P→Q)).
- normaalilla puhekielellä englanniksi Kirjoita oma kelvollinen argumenttisi vähintään kahdella toimitilalla., Argumenttisi pitäisi olla vain kappale (ei tilattu luettelo lauseista tai mitään muuta, joka näyttää muodolliselta logiikalta). Kääntää lauselogiikka logiikkaa ja todistaa, että se on voimassa käyttäen epäsuoraa johtamista.
Tämä käännös otsikko Galileo-kirja on tullut yleisin, vaikka enemmän kirjaimellinen yksi olisi ollut Diskurssit ja Matemaattinen Mielenosoituksia. Kirjan käännöksiä ovat muun muassa Drake (1974).