α-kerroin on yleisimmin käytetty menettely arvioitaessa luotettavuutta soveltavaa tutkimusta. Kuten Sijtsma (2009), sen suosio on sellainen, että työn imu (1951) on mainittu viittaus useammin kuin artikkeli löytö DNA-kaksoiskierre., Kuitenkin, sen rajoitukset ovat hyvin tiedossa (Lord ja Novick, 1968; Cortina, 1993; Yang ja Vihreä, 2011), joitakin tärkeimpiä ovat oletukset uncorrelated virheet, tau-vastaavuus-ja normaalius.
olettaen, uncorrelated virheitä (error-pisteet tahansa pari kohteita korreloi) on hypoteesi Klassisen Testata Teoriaa (Lord ja Novick, 1968), joiden rikkominen voi merkitä läsnäolo monimutkainen moniulotteinen rakenteet vaativat estimointimenetelmät, joka ottaa tämän monimutkaisuus huomioon (esim., Tarkkonen ja Vehkalahti, 2005; Vihreä ja Yang, 2015)., On tärkeää kitkeä virheellinen käsitys, että α-kerroin on hyvä indikaattori unidimensionality, koska sen arvo olisi korkeampi, jos asteikko olivat yksiulotteisia. Itse asiassa tilanne on täysin päinvastainen, kuten Sijtsma (2009) osoitti, ja sen soveltaminen tällaisissa olosuhteissa voi johtaa siihen, että luotettavuus yliarvioidaan voimakkaasti (Raykov, 2001). Näin ollen ennen α: n laskemista on tarkistettava, että tiedot sopivat unidimensionaalisiin malleihin.
oletus tau-ekvivalenssista (ts., sama true pisteet kaikki tarkastettavia kohteita, tai yhtä tekijä kuormitukset kaikki kohteet factorial-malli) on vaatimus α vastaavan luotettavuus kerroin (työn imu, 1951). Jos oletus tau-vastaavuus on rikkonut totta luotettavuuden arvo on aliarvioitu (Raykov, 1997; Graham, 2006), jonka määrä, joka voi vaihdella välillä 0,6 ja 11.1% riippuen vakavuudesta rikkomisesta (Vihreä ja Yang, 2009a). Kanssa tietoja, jotka noudattavat tätä oletusta ei yleensä ole elinkelpoinen käytännössä (Teo ja Tuuletin, 2013); sen congeneric malli (ts.,, different factor loadings) on sitä realistisempi.
vaatimus multivariant normaalius on vähemmän tunnettu ja vaikuttaa sekä puntual luotettavuuden arviointi ja mahdollisuutta perustaa luottamusvälit (Dunn et al., 2014). Sheng ja Sheng (2012) havaittiin äskettäin, että kun jakaumat ovat vinoja ja/tai leptokurtic, negatiivinen biasjännite on tuotettu, kun kerroin α on laskettu; samanlaisia tuloksia esiteltiin Vihreä ja Yang (2009b) analyysin vaikutukset ei-normaalit jakaumat arvioitaessa luotettavuutta., Skewness-ongelmien tutkiminen on tärkeämpää, kun näemme, että käytännössä tutkijat työskentelevät tavallisesti vinojen suomujen kanssa (Micceri, 1989; Norton et al., 2013; Ho and Yu, 2014). Esimerkiksi, Micceri (1989) arvioi, että noin 2/3 kyky ja yli 4/5 psychometric toimenpiteitä esillä ainakin kohtalainen epäsymmetria (eli vinous noin 1). Tästä huolimatta vinouden vaikutusta luotettavuusarvioon on tutkittu vähän.,
Ottaen huomioon, että runsaasti kirjallisuutta rajoitukset ja harhat α-kerroin (Revelle ja Zinbarg, 2009; Sijtsma, 2009, 2012; Cho ja Kim, 2015; Sijtsma ja van der Ark, 2015), herää kysymys, miksi tutkijat edelleen käyttää α, kun vaihtoehtoisia kertoimet on olemassa, joka voittaa nämä rajoitukset. On mahdollista, että viime vuosisadalla kehitetyt luotettavuuden arviointimenettelyt ovat herättäneet keskustelua. Tätä olisi entisestään lisännyt tämän kertoimen laskemisen yksinkertaisuus ja sen saatavuus kaupallisissa ohjelmistoissa.,
vaikeus arvioida pxx’ luotettavuus kerroin asuu sen määritelmä pxx’=σt2∕σx2, joka sisältää todellinen pisteet varianssi osoittaja, kun tämä on luonteeltaan muita kuin havainnoitavissa olevia. Α-kerroin yrittää lähentää tätä havaitsematonta varianssia kappaleiden tai komponenttien välisestä kovarianssista. Työn imu (1951) osoitti, että ilman tau-vastaavuus, α-kerroin (tai Guttman”s lambda 3, joka vastaa α) oli hyvä alaraja lähentämisestä., Niinpä, kun oletukset ovat rikkoneet ongelma merkitsee löytää paras mahdollinen alaraja; tämä nimi on annettu Suurin alaraja-menetelmällä (GLB), joka on paras mahdollinen arvio teoreettisesta kulma (Jackson ja Agunwamba, 1977; Woodhouse ja Jackson, 1977; Shapiro ja ten Berge, 2000; Sočan, 2000; ten Berge ja Sočan, 2004; Sijtsma, 2009). Revelle ja Zinbarg (2009) katsovat kuitenkin, että ω antaa paremman alarajan kuin GLB., On siksi avoin keskustelu siitä, mikä näistä menetelmistä antaa parhaan alaraja; lisäksi kysymys ei-normaalius ei ole tyhjentävästi tutkittu, koska nykyinen työ käsittelee.
ω Kertoimet
McDonald ’ (1999) ehdotti wt kerrointa arvioitaessa luotettavuus alkaen kertoma analyysi puitteet, joka voidaan ilmaista muodollisesti kuin:
Missä λj on lastaus kohteen j, λj2 on yhteisöllisyys kohteen j ja ψ vastaa ainutlaatuisuus., Wt kerroin, mukaan lukien lambrias sen kaavat, soveltuu sekä silloin, kun tau-vastaavuus (eli yhtä suuri tekijä kuormitukset kaikki koe-erät) on olemassa (wt sama matemaattisesti, jossa α), ja kun kohteita eri syrjintä ovat läsnä edustus rakentaa (eli eri omistautumiselle kohteita: congeneric mittaukset). Näin ollen wt korjaa aliarvioimiseen bias α, kun oletus tau-vastaavuus on rikottu (Dunn et al., 2014) ja erilaiset tutkimukset osoittavat, että se on yksi parhaista vaihtoehdoista luotettavuuden arvioimiseksi (Zinbarg et al.,, 2005, 2006; Revelle ja Zinbarg, 2009), vaikka toistaiseksi sen toiminnan edellytyksiä vinous on tuntematon.
Kun korrelaatio virheitä, tai on enemmän kuin yksi piilevä ulottuvuus tiedot, osuus kunkin ulottuvuuden total variance explained on arvioitu, saada niin sanottu hierarkkinen ω (wh), joka antaa meille mahdollisuuden korjata pahin yliarviointi bias α with multidimensional data (ks Tarkkonen ja Vehkalahti, 2005; Zinbarg et al., 2005; Revelle ja Zinbarg, 2009)., Kertoimet wh ja wt vastaavat yksiulotteisia tietoja, joten emme katso tämä kerroin yksinkertaisesti koska ω.
Suurin alaraja (GLB)
Sijtsma (2009) osoittaa useita tutkimuksia, että yksi tehokkaimmista estimaattoreita luotettavuus on GLB—päätellä Woodhouse ja Jacksonin (1977) alkaen oletukset Klassisen Testata Teoriaa (Cx = Ct + Ce)—inter-item-kovarianssi matriisin havaittu kohteen tulokset Cx. Se hajoaa kahteen osaan: summa inter-item kovarianssimatriisi kohteen todelliset tulokset Ct; ja inter-item-virheen kovarianssimatriisi Ce (ten Berge ja Sočan, 2004)., Sen ilme on:
missä σx2 on testi, varianssi-ja tr(Ce) viittaa jälkeäkään inter-item-virheen kovarianssimatriisi, joka on osoittautunut niin vaikea arvioida. Yksi ratkaisu on ollut käyttää factorial procedures kuten minimum Rank Factor Analysis (menettely tunnetaan glb.fa). Viime aikoina GLB algebraic (GLBa) – menettely on kehitetty Andreas Moltnerin laatimasta algoritmista (Moltner and Revelle, 2015)., Mukaan Revelle (2015a) tämä menettely antaa muodossa, joka on eniten uskollinen alkuperäisen määritelmän mukaan Jackson ja Agunwamba (1977), ja se on lisäetu ottaa käyttöön vektori paino kohteita merkitys (Al-Homidan, 2008).
Huolimatta sen teoreettisia vahvuuksia, GLB on käytetty hyvin vähän, vaikka jotkin viimeaikaiset empiiriset tutkimukset ovat osoittaneet, että tämä kerroin tuottaa parempia tuloksia kuin α (Lila et al., 2014) ja α Ja ω (Wilcox et al., 2014)., Kuitenkin, pieniä näytteitä, olettaen, että normaalius, se on taipumus yliarvioida todellista luotettavuutta-arvoa (Shapiro ja ten Berge, 2000), mutta sen toiminnasta ei normaalioloissa on edelleen tuntematon, erityisesti kun jakaumat kohteet ovat epäsymmetriset.
Ottaen huomioon, kertoimet edellä on määritelty, ja harhojen ja rajoitukset kunkin kohde tässä työssä on arvioida luotettavuutta näiden kertoimien läsnä epäsymmetrinen kohteita, ottaen huomioon myös oletus tau-vastaavuus ja otoskoko.,
Menetelmiä
Tietoja Sukupolvi
– tiedot on luotu käyttämällä R (R Development Core Team, 2013) ja RStudio (Racine, 2012) ohjelmisto, seuraavat kertoma malli:
missä J on simuloitu vaste kohde i kohde j, λjk on lastaus kohteen j k (joka oli luoma unifactorial malli); Fk on piilevä tekijä syntyy standardoitua normaalijakaumaa (keskiarvo on 0 ja varianssi 1), ja ej on satunnainen mittausvirhe kunkin kohteen myös seuraavat standardoitu normaalijakauma.,
Vinossa kohteita: Standardi normaali J muuttuivat tuottaa ei-normaalit jakaumat käyttäen menettelyn ehdottama Hummingbird (2002) soveltaen viidennen asteen polynomia muuttaa:
Simuloitu Olosuhteet
arvioida suorituskykyä luotettavuus kertoimet (α, ω, GLB-ja glba: n) olemme työskennelleet kolmen näytteen kokoa (250, 500, 1000), kaksi testi koot: lyhyt (6 kohdetta) ja pitkä (12 kohdetta), kaksi ehdot tau-vastaavuus (yksi tau-vastaavuus ja yksi ilman, ts.,, congeneric) ja epäsymmetristen erien asteittainen sisällyttäminen (kaikista tavanomaisista tavaroista kaikkiin epäsymmetrisiin esineisiin). Lyhyen testin luotettavuus oli asetettu 0.731, joka läsnäollessa tau-vastaavuus on saavutettu kuuden kohteita omistautumiselle = 0.558, kun congeneric malli on saatu asettamalla tekijä kuormitusten arvot 0.3, 0.4, 0.5, 0.6, 0.7, ja 0,8 (katso Liite I). 12 kappaleen pitkässä testissä luotettavuus asetettiin 0.,845 ottaen samat arvot kuin lyhyellä testi sekä tau-vastaavuus ja congeneric malli (tässä tapauksessa siellä oli kaksi kohteita kunkin arvo lambda). Näin simuloitiin 120 tilaa, joissa kussakin tapauksessa oli 1000 replikaa.
Data-Analyysi
tärkeimmät analyysit tehtiin käyttäen Psykologian (Revelle, 2015b) ja GPArotation (Bernaards ja Jennrich, 2015) – paketteja, joiden avulla α ja ω on arvioitu. GLB: n arvioinnissa käytettiin kahta tietokoneistettua lähestymistapaa: glb.fa (Revelle, 2015a) ja glb.,algebrallinen (Moltner ja Revelle, 2015), jälkimmäinen toimi kirjailijoiden, kuten Hunt ja Bentler (2015).
arvioidaksemme eri estimaattorien tarkkuutta luotettavuuden palauttamisessa laskimme juuri virheen neliötä (Rmse) ja harhaa. Ensimmäinen on eroja arvioitu ja simuloitu luotettavuus ja on virallistettu niin:
missä ρ^ on arvioitu luotettavuus kunkin kertoimen ρ simuloitu luotettavuus ja Nr määrä jäljennöksiä., N % bias ymmärretään ero keskiarvo arvioitu luotettavuus ja simuloitu luotettavuus ja on määritelty seuraavasti:
molemmat indeksit, suurempi arvo, sitä suurempi epätarkkuus arviointityökalu, mutta toisin kuin RMSE, bias voi olla positiivinen tai negatiivinen; tässä tapauksessa ylimääräistä tietoa olisi saatu, onko kerroin on aliarvioi tai yliarvioi simuloitu luotettavuuden parametri., Suosituksesta Hoogland ja Boomsma (1998) arvot RMSE < 0,05 ja % bias < 5% oli pitää hyväksyttävänä.
Tulokset
tärkeimmät tulokset on nähtävissä Taulukossa 1 (6 kohdetta) ja Taulukossa 2 (12 kohdetta). Nämä osoittavat RMSE ja % bias kertoimien tau-vastaavuus-ja congeneric ehtoja, ja miten vinous testin jakelu kasvaa asteittainen sisällyttäminen epäsymmetrinen kohteita.
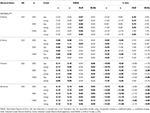
Taulukossa 1., RMSE ja Bias tau-vastaavuus-ja congeneric edellytys 6 kohdetta, kolme näyte koot ja määrä vinossa kohteita.
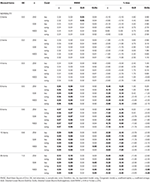
Taulukossa 2. RMSE ja Bias tau-vastaavuus-ja congeneric edellytys 12 kohdetta, kolme näyte koot ja määrä vinossa kohteita.
Vain olosuhteissa, tau-vastaavuus ja normaaliuden (skewness < 0.2) on havaittu, että α-kertoimella arvioiden simuloitu luotettavuus oikein, kuten ω., Kongeneerisessa tilassa ω korjaa α: n aliarvioinnin. Molemmat GLB ja glba: n nykyinen positiivinen bias alle normaaliuden kuitenkin osoittaa, glba: n noin ½ vähemmän % bias kuin GLB (ks. Taulukko 1). Jos tarkastelemme näytteen kokoa, huomaamme, että testikoon kasvaessa Glb: n ja GLBa: n positiivinen bias pienenee, mutta ei koskaan katoa.
epäsymmetrinen ehtoja, me katso Taulukko 1 sekä α ja ω aiheudu kohtuutonta suorituskyky kasvaa RMSE ja underestimations joka voi olla harhaa > 13% α-kerroin (välillä 1 ja 2 prosenttia pienempi ω)., GLB ja glba: n kertoimia hetkellä pienempi RMSE kun testi vinous tai määrä epäsymmetrinen kohdetta lisää (ks. Taulukot 1, 2). GLB kerroin esittelee paremmat arviot, kun testi vinous-arvo testi on noin 0.30; glba: n on hyvin samanlainen, esittää parempia arvioita kuin ω, jossa on testi vinous-arvo noin 0.20 tai 0.30. Kuitenkin, kun vinous-arvo kasvaa 0,50 tai 0.60, GLB esittelee paremman suorituskyvyn kuin glba: n. Testin koko (6 tai 12 ítems) on paljon tärkeämpi vaikutus kuin otoksen koko on arvioiden tarkkuutta.,
Keskustelua
tässä tutkimuksessa neljä tekijää olivat manipuloitu: tau-vastaavuus tai congeneric malli, otoksen koko (250, 500, ja 1000), määrä tarkastettavia kohteita (6 ja 12) ja määrä epäsymmetrinen kohteita (0 epäsymmetrinen kohteita kaikki kohteet on epäsymmetrinen), jotta voidaan arvioida luotettavuutta läsnäolo epäsymmetrinen tiedot neljä luotettavuus kertoimet analysoitu. Näitä tuloksia käsitellään jäljempänä.,
edellytyksiä tau-vastaavuus, α ja ω kertoimet toisiaan, kuitenkin ilman tau-vastaavuus (congeneric), ω aina esittää parempia arvioita ja pienempi RMSE ja % bias kuin α. Tässä realistisempi kunnossa vuoksi (Vihreä ja Yang, 2009a; Yang ja Vihreä, 2011), α tulee negatiivisesti puolueellinen luotettavuus estimaattori (Graham, 2006; Sijtsma, 2009; Cho ja Kim, 2015) ja ω on aina parempi α (Dunn et al., 2014). Tapauksessa ei-vastoin oletusta normaaliuden, ω on paras estimaattori kaikki kertoimet arvioidaan (Revelle ja Zinbarg, 2009).,
Turning otoskoko, huomaamme, että tämä tekijä on pieni vaikutus alle normaaliuden tai hieman poikkeaa normaaliuden: n RMSE ja bias vähenevät, kun otoskoko kasvaa. Kuitenkin, se voi olla sanoi, että näiden kahden kertoimia, joilla otos koko 250 ja normaaliuden saadaan suhteellisen tarkkoja arvioita (Tang ja Cui, 2012; Javali et al., 2011)., Sillä GLB ja glba: n kertoimia, koska otoskoko lisää RMSE ja bias yleensä heikentää; kuitenkin he säilyttää positiivinen bias kunto normaaliuden vaikka suurten otoskokojen 1000 (Shapiro ja ten Berge, 2000; ten Berge ja Sočan, 2004; Sijtsma, 2009).
testissä kokoa ei yleensä tarkkailla korkeampi RMSE ja bias 6 kohdetta kuin 12, mikä viittaa siihen, että suurempi määrä kohteita, pienempi RMSE ja bias-estimaattoreita (Cortina, 1993). Yleensä suuntaus säilyy sekä 6 että 12 kohdassa.,
Kun tarkastelemme vaikutus asteittain joissa epäsymmetrinen kohteet data set, voimme todeta, että α-kerroin on erittäin herkkä epäsymmetrinen kohteet; nämä tulokset ovat samanlaisia kuin löytyy Sheng ja Sheng (2012) ja Vihreä ja Yang (2009b). Kerroin ω esittää samankaltaisia RMSE-ja bias-arvoja kuin α, mutta hieman parempia, jopa tau-ekvivalenssilla. GLB-ja glba: n on todettu aiheuttavan paremmat arviot, kun testi vinous poikkeaa arvot ovat lähellä 0.
ottaen huomioon, että käytännössä on tavallista löytää epäsymmetristä dataa (Micceri, 1989; Norton et al.,, 2013; Ho and Yu, 2014), Sijtsma”s suggestion (2009) Glb: n käyttämisestä luotettavuusarvioijana vaikuttaa perustellulta. Muut tekijät, kuten Revelle ja Zinbarg (2009) ja Vihreä ja Yang (2009a), suosittelemme käytettäväksi ω, kuitenkin tämä kerroin vain tuottanut hyviä tuloksia kunnon normaaliuden, tai joilla on alhainen osuus vinous kohteita. Joka tapauksessa nämä kertoimet esittivät suurempia teoreettisia ja empiirisiä etuja kuin α. Suosittelemme kuitenkin tutkijoita tutkimaan täsmällisten arvioiden lisäksi myös intervalliarvioinnin hyödyntämistä (Dunn ym., 2014).,
nämä tulokset rajoittuvat simuloituihin olosuhteisiin ja oletetaan, että virheiden välillä ei ole korrelaatiota. Tämä olisi tarpeen suorittaa lisätutkimuksia arvioida toimintaa eri luotettavuus-kertoimien kanssa enemmän monimutkainen moniulotteinen rakenteiden (Reise, 2012; Vihreä ja Yang, 2015) ja läsnä järjestysluku ja/tai kategorinen data, jossa ei noudateta oletus normaaliuden normi.
päätelmä
kun testin kokonaispisteet jaetaan normaalisti (ts., kaikki tuotteet ovat normaalisti jakautunut) ω pitäisi olla ensimmäinen valinta, jonka jälkeen α, koska he välttää yliarviointi esittämiä ongelmia GLB. Kuitenkin, kun on alhainen tai kohtalainen testi vartaassa GLBa on käytettävä. GLB on suositeltavaa, kun osuus epäsymmetrinen kohteita on korkea, koska näissä olosuhteissa käyttää sekä α ja ω luotettavuus estimaattoreita ei ole suositeltavaa, mitä otoskoko.
Kirjailijasuoritukset
tutkimus-ja teoreettisen viitekehyksen idean kehittäminen (IT, JA). Menetelmäkehyksen rakentaminen (IT, JA)., R-kielen syntaksin kehittäminen (IT, JA). Tietojen analysointi ja tulkinta (IT, JA). Tulosten tarkastelu nykyisen teoreettisen taustan valossa (JA, IT). Artikkelin valmistelu ja kirjoittaminen (JA, IT). Yleisesti ottaen molemmat kirjoittajat ovat osallistuneet tasapuolisesti tämän teoksen kehittämiseen.,
Rahoitus
ensimmäinen kirjoittaja paljastaa vastaanottamisesta seuraavat taloudellista tukea tutkimus -, laatija, ja/tai julkaisemisesta tämän artikkelin: SE sai rahallista tukea Chilen Kansallisen Komission Tieteellinen ja Teknologinen Tutkimus (CONICYT) ”Becas Chile” Jatko-Fellowship-ohjelma (Grant nro: 72140548).
eturistiriita Lausunto
kirjoittajat ilmoittavat, että tutkimus on tehty ilman mitään kaupallisia tai taloudellisia suhteita, jotka voitaisiin tulkita mahdollisia eturistiriitoja.
Cronbach, L. (1951)., Kerroin alfa ja testien sisäinen rakenne. Psykometrika 16, 297-334. doi: 10.1007/BF02310555
CrossRef Koko Teksti | Google Scholar
McDonald, R. (1999). Testiteoria: yhtenäinen hoito. Mahwah, NJ: Lawrence Erlbaum Associates.
Google Scholar
R Development Core Team (2013). R: Tilastolaskennan kieli ja ympäristö. Wien: R Tilastolaskennan säätiö.
Raykov, T. (1997)., Scale reliability, cronbach”s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package ”psych.,”Saatavilla verkossa osoitteessa: http://org/r/psych-manual.pdf
Shapiro, A., ja ten Berge, J. M. F. (2000). Asymptoottinen bias vähintään trace factor analyysi, sovellusten suurin pienempi sidottu luotettavuuteen. Psykometrika 65, 413-425. doi: 10.1007/BF02296154
CrossRef Koko Teksti | Google Scholar
ten Berge, J. M. F., ja Sočan, G. (2004). Suurin alempi sidos testin luotettavuuteen ja epäidimensionaalisuuden hypoteesiin. Psykometrika 69, 613-625. doi: 10.,1007/BF02289858
CrossRef Koko Teksti | Google Scholar
Woodhouse, B., ja Jackson, P. H. (1977). Alarajojen luotettavuus pisteet testi, joka koostuu ei-homogeeninen kohteita: II: haku etsiä suurin alaraja. Psykometrika 42, 579-591. doi: 10.1007/BF02295980
CrossRef Koko Teksti | Google Scholar
Liite I
T-syntaksia arvioida luotettavuutta kertoimet Pearson”s korrelaatio matriisit., Korrelaatio arvojen ulkopuolella lävistäjä lasketaan kertomalla tekijä lastaus kohteita: (1) tau-vastaava malli ne ovat kaikki yhtä 0.3114 (λiλj = 0.558 × 0.558 = 0.3114) ja (2) congeneric malli ne vaihtelevat funktiona eri tekijä lastaus (esim. matriisi-elementti a1, 2 = λ1λ2 = 0.3 × 0.4 = 0.12). Molemmissa esimerkeissä todellinen luotettavuus on 0,731.
> omega(Cr,1)$alpha # standardoitu työn imu”s α
0.731
> omega(Cr,1)$omega.tot # kerroin ω yhteensä
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach”s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731