”olen joka tapauksessa vakuuttunut siitä, että Hän ei heitä noppaa.,”
~ Albert Einstein
- Random Muuttujia
- Diskreettejä satunnaismuuttujia
- Jatkuva satunnaismuuttujat
- Satunnainen Sekoitettu Muuttujat
- Kumulatiivinen Jakauma (CDF)
- todennäköisyystiheysfunktion (PDF)
- Vuorovaikutteinen CDF – /PDF-Esimerkki
satunnaismuuttujia:

Sano, että olit ottaa kolikon taskustaan ja heitti sen ilmaan. Mitä voisit sanoa sen tulevaisuudesta?
nouseeko se maihin? Klaava?, Kauanko se pysyy ilmassa? Montako kertaa se pomppii? Kuinka kaukana siitä, missä se ensin osuu maahan, se lopulta lepää? Osuuko se koskaan maahan? Oletko koskaan tullut lepäämään?
joillekin tällaisille kysymyksille voimme ja tyydymme vastauksiin jo kauan ennen havaintoja; olemme melko varmoja, että painovoima pitää ja kolikko laskeutuu. Mutta muille Meillä ei ole muuta vaihtoehtoa kuin arvostella ja puhua epämääräisemmin, jos haluamme sanoa mitään hyödyllistä tulevaisuudesta lainkaan.,
tutkijoina meidän tehtävämme on tietysti sanoa jotain hyödyllistä (tai vähintäänkin arvovaltaista…), vaikka tärkeän fyysisen järjestelmän metaforiset kolikot ovat vielä ilmassa. Kruuna tai klaava voi olla jopa elämän tai kuoleman kysymys. Kolikkomme voivat olla esimerkiksi erilaiset mahdolliset jäähdytysnesteen virtausnopeudet tai uraanimassat ydinvoimalassa. Välitämme suuresti tietää, mikä on mahdollisuutemme, että saamme pyöriviä turbiineja sulamisen sijaan.,
tiukalle deterministille kaikki tällaiset vedot ratkaistiin kauan ennen kuin mitään kolikkoa, metaforista tai ei, lyötiin; emme yksinkertaisesti vielä tiedä sitä. Kunpa tietäisimme vain kolikon heitossa käytetyt voimat, sen tarkan massan jakautumisen, huoneen eri minuuttien ilmanliikkeet… Jos tietäisimme kaiken tuon, tietäisimme, että tietyllä kolikonheitolla oli 100 prosentin mahdollisuus laskeutua niin kuin se laskeutuu, ja nolla mahdollisuutta mihinkään muuhun lopputulokseen.
mutta meiltä tietysti puuttuu usein edes mitattavissa oleva murto-osa tällaisesta maailman tuntemuksesta., Lisäksi näyttää siltä, on tavattoman pieni asteikot, jotka tiukkaa determinists ovat ehdottomasti väärin; ei ole mitään keinoa ennustaa, kun esimerkiksi uraanin atomi on halkaistu, ja jos tällainen tapahtuma vaikuttaa laajemmin maailmassa niin, että makro tapahtuma on todella arvaamaton. Jotkut tulokset todella ovat ilmassa, levoton, kunnes ne ovat osa menneisyyttä.
selviytyäksemme tästä todellisuudesta ja kyetäksemme kuvaamaan järjestelmän tulevia tiloja jollain hyödyllisellä tavalla, käytämme satunnaismuuttujia., Satunnaismuuttuja on yksinkertaisesti funktio, joka liittää järjestelmän jokaisen mahdollisen fyysisen tuloksen johonkin ainutlaatuiseen, reaalilukuun. Sellaisenaan on olemassa kolmenlaisia satunnaismuuttujia: diskreetti, jatkuva ja sekoitettu. Seuraavissa kohdissa käsitellään lyhyesti näitä luokkia ja annetaan esimerkkejä.
diskreetit satunnaismuuttujat:
harkitse kolikonheittoa uudelleen. Meillä voisi olla kruuna tai klaava mahdollisina tuloksina. Jos me määritellään muuttuja, x, koska määrä päät yhteen nakata, niin x voisi mahdollisesti olla 1 tai 0, ei mitään muuta., Tällainen funktio x olisi esimerkki diskreetistä satunnaismuuttujasta. Tällaiset satunnaismuuttujat voivat ottaa vain diskreettejä arvoja. Muita esimerkkejä olisivat raskaustestin mahdolliset tulokset tai oppilasmäärä luokkahuoneessa.
jatkuvatoimiset satunnaismuuttujat:
takaisin kolikonheittoon, mitä jos haluaisimmekin kuvailla etäisyyttä siihen, missä kolikko tuli lepäämään ja missä se ensin osui maahan. Se etäisyys, x, olisi jatkuva satunnaismuuttuja, koska se voisi ottaa ääretön määrä arvoja jatkuva välillä todellinen määrä., Kolikko voi kulkea 1 cm tai 1,1 cm tai 1,11 cm, tai päälle ja päälle. Muita esimerkkejä satunnaiset muuttujat olisi massa tähdet galaksimme, pH valtameren vedet, tai viipymäaika joitakin tutkittavan aineen määrän kaasukromatografi.
Sekamuuttujat:
Sekamuuttujilla on sekä diskreettejä että jatkuvia komponentteja. Tällaisia satunnaismuuttujia esiintyy harvoin. Mahdollisessa esimerkissä voidaan kuitenkin mitata näytteen painoa ja päättää, että negatiivisena arvona mitatulle painolle annetaan arvo 0., Siten satunnaismuuttuja on diskreetti komponentti x = 0 ja jatkuva osa, jossa x > 0.
Kumulatiivinen Jakauma (CDF):
kysymykseen, tietenkin, kysymys siitä, miten parhaiten matemaattisesti kuvata (ja visuaalisesti näyttö) satunnaismuuttujia. Näihin tehtäviin käytämme todennäköisyystiheysfunktioita (PDF) ja kumulatiivisia tiheysfunktioita (CDF). Kuten CDFs on helpompi ymmärtää sekä diskreettejä ja jatkuvia satunnaismuuttujia kuin Pdf-tiedostoissa, meidän on ensin selittää, CDFs.
harkitse reilun 6-sivuisen nopan heittämistä., Meillä olisi 1: 6 mahdollisuus saada jokin satunnaismuuttujan mahdollisista arvoista (1, 2, 3, 4, 5, tai 6). Jos me piirtää ne mahdolliset arvot x-akselille ja tontin todennäköisyys mittaus kunkin arvo, x, tai mikä tahansa arvo, joka on pienempi x-y-akselilla, meillä on CDF-satunnainen muuttuja.
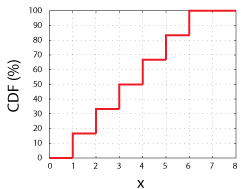
CDF Oikeudenmukaisen 6-Sidded Noppaa. Huomaa, että jokainen askel on korkeus 16,67%, tai 1 6.
tämä funktio, CDF(x), kertoo yksinkertaisesti todennäköisyydet mitata mikä tahansa arvo x: ään asti ja mukaan lukien., Kuten kaikki CDFs on kaikki nämä ominaisuudet:
- CDF-on yhtä suuri kuin 0, kun x = -∞, ja lähestymistapa 1 (tai 100%), kun x lähestyy +∞. Yksinkertaisesti sanottuna, kaikista mahdollisista tuloksista, on oltava tulos; mahdollisuus heittää kuusisivuinen noppaa ja saada arvo välillä -∞ ja ∞ on 100%.
- CDF: n kaltevuuden on aina oltava yhtä suuri tai suurempi kuin nolla. Harkitse esimerkiksi mahdollisuutta heittää 6-sivuinen noppaa (reilu tai ei) ja saada arvo välillä 0 ja 4., Sitä mahdollisuutta ei voi olla enemmän kuin tilaisuus saada arvon välillä 0 ja 5, koska kertoimet 1, 2, tai 3 lasku kasvot ovat, tietenkin, aina tulee olemaan joitakin osa todennäköisyys saada 1, 2, 3, tai 4.
esimerkki jatkuva satunnaismuuttuja, seuraava sovelma näyttää normaalisti jakautunut CDF.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Huomaa vain, että ominaisuudet CDF kuvattu edellä ja selitetty diskreetti satunnaismuuttuja pitää jatkuva satunnaismuuttujat samoin.
Lisää intuitiivisia esimerkkejä CDFs: n ominaisuuksista on seuraavassa interaktiivisessa esimerkissä. Myös monien muiden tilastoalalle tärkeiden ja tällä sivustolla käytettävien CDF-levyjen Interaktiiviset palstat löytyvät täältä.
Todennäköisyys Tiheys Toiminnot (PDF):
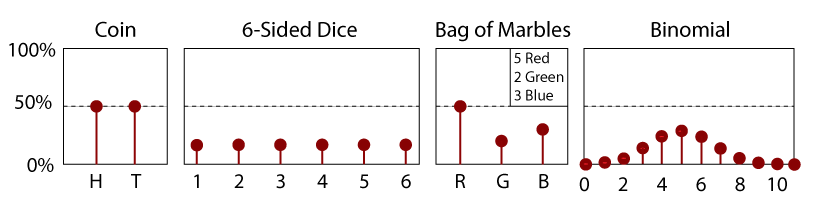
PDF Reilu 6-Sidded Noppaa.
PDF on yksinkertaisesti CDF: n derivaatta., Näin ollen PDF on myös satunnaismuuttujan, x, funktio, ja sen suuruus on jokin osoitus tietyn arvon mittaamisen suhteellisesta todennäköisyydestä. Koska se on kaltevuus CDF, PDF on aina oltava positiivinen; ei ole negatiivisia kertoimia missään tapauksessa. Lisäksi ja määritelmällisesti PDF(x) – ∞ – ja x-käyrän alla oleva alue on yhtä kuin sen CDF(x). Tällöin kahden arvon x1 ja x2 välinen alue antaa todennäköisyyden mitata arvo kyseisellä alueella.
seuraava sovelma näyttää esimerkkiä PDF on normaalisti jakautunut satunnaismuuttuja, x.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., tarkastellaan myös jatkuvan ja diskreetin PDF: n eroa. Vaikka diskreetti PDF (kuten edellä dice) antaa sinulle kertoimet saada tietyn tuloksen, todennäköisyydet jatkuva pdf ovat asioita alue, ei diskreetti pistettä. Esimerkiksi, on selvästi 1 6 (16.6%) mahdollisuus liikkuvan 3 dice, kuten voidaan nähdä sen PDF. Mutta mitä on outoa mitata täsmälleen nolla satunnaismuuttujan kanssa, jolla on normaali PDF ja keskiarvo nolla, kuten edellä on esitetty? Vaikka se on arvo, jossa PDF on suurin, mahdollisuus mitata juuri 0.00000..,. on, ehkä laskuri intuitiivisesti, nolla. Todennäköisyys mitata jokin tietty satunnaisluku äärettömään tarkkuuteen on itse asiassa nolla. jatkuva PDF voi sen sijaan kysyä, mitä kertoimet ovat, että voit mitata kahden arvon välillä saada todennäköisyydellä, joka on suurempi kuin nolla. Löytääksemme tämän todennäköisyyden käytämme vain satunnaismuuttujamme CDF: ää., Koska CDF kertoo meille outoa mittaus-arvo tai jotain pienempi kuin arvo, löytää todennäköisyys mittaus välillä kaksi arvoa, x1 ja x2 (jos x1 > x2), me yksinkertaisesti on otettava arvo CDF klo x1 ja vähennä sen arvoa CDF klo x2. Esimerkiksi, käyttäen normaali CDF-applet yläpuolella (jossa μ=0 ja σ=1), jos halusimme tietää kertoimet mitata välillä 0,01 ja 0,02 löydämme CDF(x=0.1)=53.9828% ja CDF(x=0.2)=57.9260%. Sitten ero, CDF(0.2)-CDF(0.1), antaa meille kertoimet noin 3,9% mittaus x välillä 0.1 ja 0.2., intuitiivisemmat visuaaliset esimerkit PDF-tiedostojen ominaisuuksista ovat seuraavassa interaktiivisessa esimerkissä. Myös, interaktiivinen tontteja monia tärkeitä PDF käytetään tällä sivustolla voidaan nähdä täällä. |
|||||||||||||||||