Sisältö – Todennäköisyys tiheys toiminnot

Sisältö

Todennäköisyys tiheys toiminnot

todennäköisyystiheysfunktion (pdf) \(f(x)\) on jatkuva satunnaismuuttuja \(X\) on määritelty johdannainen cdf \(F(x)\):

\

joskus on hyödyllistä pohtia cdf \(F(x)\) suhteen pdf \(f(x)\):

\

pdf – \(f(x)\) on kaksi tärkeää ominaisuuksia:

1. \(f(x) \geq 0\), kaikilla \(x\)
2. \(\displaystyle\int_{-\infty}^{\infty} f(x)\;dx = 1\).,

ääretön erilaisia muotoja on mahdollista, että pdf-tiedosto, koska ainoat vaatimukset ovat kaksi ominaisuuksia edellä. Pdf voi olla yksi tai useita huiput, tai ei huiput ollenkaan; se voi olla epäjatkuvuuksia, koostuu yhdistelmiä toimintoja, ja niin edelleen. kuvassa 5 on pdf, jossa on yksi huippu ja hieman lievä vinous. Kuten tyypillinen pdf, funktion arvo lähestyy nollaa, kun \(x \to \infty\) ja \(x \to\infty\).

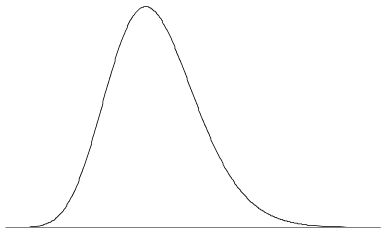
Kuva 5: pdf-tiedosto voi näyttää tältä.,

nyt selvitetään, miten jatkuvan satunnaismuuttujan todennäköisyydet \(X\) liittyvät sen pdf-muotoon. Tärkeä tulos tässä on se, että

\_a^b.\]

Tämä tulos seuraa siitä, että molemmat osapuolet ovat yhtä kuin \(F(b) – F(a)\).

nuotit.

• jatkuva satunnaismuuttuja, meidän on otettava huomioon todennäköisyys, että se on väli. Merkitystä tähän tulokseen on se, että se kertoo meille, että, löydät todennäköisyys, meidän täytyy löytää ala pdf antanut välein.
• kokonaispinta-ala pdf: n alla on 1., Niin, tämä tulos kertoo, että arvioitu todennäköisyys, että satunnainen muuttuja on tietyn välein, meidän täytyy vain arvata osa-alueen alla pdf-päiden välillä välein.
• tämä tulos antaa toisen näkökulman siihen, miksi PDF-tiedostot eivät voi olla negatiivisia, koska jos ne olisivat, voitaisiin saada negatiivinen todennäköisyys, mikä on mahdotonta.
• pdf on analoginen, mutta erilainen kuin diskreetin satunnaismuuttujan todennäköisyysfunktio (PF). Pf antaa todennäköisyyden, joten se ei voi olla yhtä suurempi., Pdf – \(f(x)\), kuitenkin, voi antaa arvo, joka on suurempi kuin yksi joitakin arvoja \(x\), koska se ei ole arvo \(f(x)\), mutta alle jäävä pinta-ala, joka edustaa todennäköisyys. Toisaalta käyrän korkeus heijastaa suhteellista todennäköisyyttä. Jos \(f(b) = 2f(a)\), niin havainto lähellä \(b\) on noin kaksi kertaa todennäköisemmin kuin havainto lähellä \(a\).,

Seuraava sivu – Sisältö – Keskiarvo ja varianssi jatkuvan satunnaismuuttujan