Le coefficient α est la procédure la plus utilisée pour estimer la fiabilité en recherche appliquée. Comme indiqué par Sijtsma (2009), sa popularité est telle que Cronbach (1951) a été cité comme référence plus fréquemment que l’article sur la découverte de la double hélice D’ADN., Néanmoins, ses limites sont bien connues (Lord et Novick, 1968; Cortina, 1993; Yang et Green, 2011), certaines des plus importantes étant les hypothèses d’erreurs non corrélées, d’équivalence tau et de normalité.
l’hypothèse d’erreurs non corrélées (le score d’erreur de toute paire d’éléments n’est pas corrélé) est une hypothèse de la théorie classique des tests (Lord et Novick, 1968), dont la violation peut impliquer la présence de structures multidimensionnelles complexes nécessitant des procédures d’estimation prenant en compte cette complexité (par exemple, Tarkkonen et Vehkalahti, 2005; Green et Yang, 2015)., Il est important de déraciner la croyance erronée que le coefficient α est un bon indicateur d’unidimensionnalité car sa valeur serait plus élevée si l’échelle était unidimensionnelle. En fait, c’est exactement le contraire, comme l’a montré Sijtsma (2009), et son application dans de telles conditions peut conduire à une surestimation importante de la fiabilité (Raykov, 2001). Par conséquent, avant de calculer α, il est nécessaire de vérifier que les données correspondent à des modèles unidimensionnels.
l’hypothèse de l’équivalence tau (c.-à-d.,, le même score vrai pour tous les éléments de test, ou des charges factorielles égales de tous les éléments d’un modèle factoriel) est une exigence pour que α soit équivalent au coefficient de fiabilité (Cronbach, 1951). Si l’hypothèse de l’équivalence tau est violée, la valeur réelle de fiabilité sera sous-estimée (Raykov, 1997; Graham, 2006) d’un montant qui peut varier entre 0,6 et 11,1% selon la gravité de la violation (Green et Yang, 2009a). Travailler avec des données conformes à cette hypothèse n’est généralement pas viable dans la pratique (Teo et Fan, 2013); le modèle congénère (c.-à-d.,, différents facteurs de charge) est le plus réaliste.
l’exigence de normalité multivariante est moins connue et affecte à la fois l’estimation de la fiabilité ponctuelle et la possibilité d’établir des intervalles de confiance (Dunn et al., 2014). Sheng et Sheng (2012) ont observé récemment que lorsque les distributions sont biaisées et/ou leptokurtiques, un biais négatif est produit lorsque le coefficient α est calculé; des résultats similaires ont été présentés par Green et Yang (2009b) dans une analyse des effets des distributions non normales dans l’estimation de la fiabilité., L’étude des problèmes d’asymétrie est plus importante lorsque nous voyons que, dans la pratique, les chercheurs travaillent habituellement avec des échelles asymétriques (Micceri, 1989; Norton et al., 2013; Ho et Yu, 2014). Par exemple, Micceri (1989) a estimé qu’environ 2/3 de la capacité et plus de 4/5 des mesures psychométriques présentaient une asymétrie au moins modérée (c’est-à-dire une asymétrie autour de 1). Malgré cela, l’impact de l’asymétrie sur l’estimation de la fiabilité a été peu étudié.,
compte tenu de la littérature abondante sur les limites et les biais du coefficient α (Revelle et Zinbarg, 2009; Sijtsma, 2009, 2012; Cho et Kim, 2015; sijtsma et van der Ark, 2015), la question se pose de savoir pourquoi les chercheurs continuent d’utiliser α lorsqu’il existe des coefficients alternatifs qui surmontent ces limitations. Il est possible que l’excès de procédures d’estimation de la fiabilité développées au siècle dernier ait attisé le débat. Cela aurait été encore aggravé par la simplicité du calcul de ce coefficient et sa disponibilité dans les logiciels commerciaux.,
la difficulté d’estimer le coefficient de fiabilité de pxx réside dans sa définition pxx’=σt2∕σx2, qui inclut le score vrai dans le numérateur de variance lorsque celui-ci est par nature inobservable. Le coefficient α tente d’approximer cette variance inobservable de la covariance entre les éléments ou les composantes. Cronbach (1951) a montré qu’en l’absence d’équivalence tau, le coefficient α (ou Lambda 3 de Guttman, qui est équivalent à α) était une bonne approximation de la borne inférieure., Ainsi, lorsque les hypothèses sont violées, le problème se traduit par la recherche de la meilleure borne inférieure possible; en effet, ce nom est donné à la méthode de la plus grande borne inférieure (GLB) qui est la meilleure approximation possible sous un angle théorique (Jackson et Agunwamba, 1977; Woodhouse et Jackson, 1977; Shapiro et ten Berge, 2000; Sočan, 2000; ten Berge et Sočan, 2004; Sijtsma, 2009). Cependant, Revelle et Zinbarg (2009) considèrent que ω donne une meilleure borne inférieure que GLB., Il y a donc un débat non résolu quant à savoir laquelle de ces deux méthodes donne la meilleure limite inférieure; de plus, la question de la non-normalité n’a pas été étudiée de manière exhaustive, comme l’explique le présent travail.
ω Coefficients
McDonald (1999) a proposé le coefficient wt pour estimer la fiabilité à partir d’un cadre d’analyse factorielle, qui peut être exprimé formellement comme suit:
où λj est la charge de l’élément j, λj2 est la communalité de l’élément j et ψ équivaut à l’unicité., Le coefficient wt, en incluant les lambdas dans ses formules, convient à la fois lorsque l’équivalence tau (c’est-à-dire des charges de facteur égales de tous les éléments de test) existe (wt coïncide mathématiquement Avec α) et lorsque des éléments avec différentes discriminations sont présents dans la représentation de la construction (c’est-à-dire des charges de facteur différentes Par conséquent, wt corrige le biais de sous-estimation de α lorsque l’hypothèse de l’équivalence tau est violée (Dunn et al., 2014) et différentes études montrent qu’il s’agit de l’une des meilleures alternatives pour estimer la fiabilité (Zinbarg et al.,, 2005, 2006; Revelle et Zinbarg, 2009), bien qu’à ce jour son fonctionnement dans des conditions d’asymétrie soit inconnu.
Lorsqu’il existe une corrélation entre les erreurs, ou qu’il y a plus d’une dimension latente dans les données, la contribution de chaque dimension à la variance totale expliquée est estimée, obtenant le ω (WH) dit hiérarchique qui nous permet de corriger le pire biais de surestimation de α avec des données multidimensionnelles (voir Tarkkonen et Vehkalahti, 2005; Zinbarg et al., 2005; Revelle et Zinbarg, 2009)., Les Coefficients wh et wt sont équivalents en données unidimensionnelles, nous appellerons donc ce coefficient simplement ω.
Greatest Lower Bound (GLB)
Sijtsma (2009) montre dans une série d’études que L’un des estimateurs de fiabilité les plus puissants est GLB—déduit par Woodhouse et Jackson (1977) à partir des hypothèses de la théorie des tests classiques (Cx = Ct + Ce)—une matrice de covariance inter-items pour les scores d’items observés Cx. Il se décompose en deux parties: la somme de la matrice de covariance inter-items pour les scores réels items Ct; et la matrice de covariance d’erreur inter-items Ce (ten Berge et Sočan, 2004)., Son expression est:
où σx2 est la variance de test et tr(ce) fait référence à la trace de la matrice de covariance d’erreur inter-items qu’il s’est avéré si difficile d’estimer. Une solution a été d’utiliser des procédures factorielles telles que L’Analyse Factorielle de rang Minimum (une procédure connue sous le nom de glb.fa). Plus récemment, la procédure algébrique GLB (GLBa) a été développée à partir d’un algorithme conçu par Andreas Moltner (Moltner et Revelle, 2015)., Selon Revelle (2015a), cette procédure adopte la forme la plus fidèle à la définition originale de Jackson et Agunwamba (1977), et elle présente l’avantage supplémentaire d’introduire un vecteur pour pondérer les éléments par importance (Al-Homidan, 2008).
malgré ses atouts théoriques, le GLB a été très peu utilisé, bien que certaines études empiriques récentes aient montré que ce coefficient produit de meilleurs résultats que α (Lila et al., 2014) et α et ω (Wilcox et coll., 2014)., Néanmoins, dans de petits échantillons, sous l’hypothèse de la normalité, il a tendance à surestimer la valeur de fiabilité réelle (Shapiro et ten Berge, 2000); cependant, son fonctionnement dans des conditions non normales reste inconnu, en particulier lorsque les distributions des éléments sont asymétriques.
compte tenu des coefficients définis ci-dessus, et des biais et limites de chacun, l’objet de ce travail est d’évaluer la robustesse de ces coefficients en présence d’éléments asymétriques, en considérant également l’hypothèse d’équivalence tau et la taille de l’échantillon.,
méthodes
génération de données
Les données ont été générées à L’aide du logiciel R (R Development Core Team, 2013) et RStudio (Racine, 2012), suivant le modèle factoriel:
ij est la réponse simulée du sujet i dans l’élément J, λjk est le chargement de l’élément J dans le facteur K (qui a été généré par le modèle unifactoriel); FK est le facteur latent généré par une distribution normale normalisée (moyenne 0 et variance 1), et EJ est L’erreur de mesure aléatoire de chaque élément suivant également une distribution normale normalisée.,
éléments asymétriques: les Xij normales Standard ont été transformées pour générer des distributions non normales en utilisant la procédure proposée par Headrick (2002) en appliquant des transformations polynomiales du cinquième ordre:
oefficients (α, ω, GLB et GLBA) nous avons travaillé avec trois tailles d’échantillon (250, 500, 1000), deux tailles de test: Court (6 Items) et long (12 items), deux conditions D’équivalence Tau (une avec équivalence Tau et une sans, c’est-à-dire,, congénère) et l’incorporation progressive d’éléments asymétriques (de tous les éléments étant normaux à tous les éléments étant asymétriques). Dans le test court, la fiabilité a été fixée à 0,731, ce qui, en présence d’équivalence tau, est obtenu avec six éléments avec des charges factorielles = 0,558; tandis que le modèle congénère est obtenu en fixant des charges factorielles à des valeurs de 0.3, 0.4, 0.5, 0.6, 0.7, et 0,8 (voir Appendice I). Dans le long test de 12 articles, la fiabilité a été fixée à 0.,845 en prenant les mêmes valeurs que dans le test court pour l’équivalence tau et le modèle congénère (dans ce cas, il y avait deux éléments pour chaque valeur de lambda). De cette façon, 120 conditions ont été simulées avec 1000 répliques dans chaque cas.
analyse des données
Les principales analyses ont été réalisées à l’aide des paquets Psych (Revelle, 2015b) et GPArotation (Bernaards et Jennrich, 2015), qui permettent d’estimer α Et ω. Deux approches informatisées ont été utilisées pour estimer les GLB: glb.fa (Revelle, 2015a) et glb.,algébrique (Moltner et Revelle, 2015), ce dernier a travaillé par des auteurs comme Hunt et Bentler (2015).
afin d’évaluer la précision des différents estimateurs dans la récupération de la fiabilité, nous avons calculé le carré D’erreur moyen racine (RMSE) et le biais. La première est la moyenne des différences entre la fiabilité estimée et la fiabilité simulée et est formalisée comme suit:
Où ρ^ est la fiabilité estimée pour chaque coefficient, ρ la fiabilité simulée et Nr le nombre de répliques., Le % de biais est compris comme la différence entre la moyenne de la fiabilité estimée et la fiabilité simulée et est défini comme suit:
dans les deux indices, Plus la valeur est élevée, plus l’inexactitude de l’estimateur est grande, mais contrairement au RMSE, le biais peut être positif ou négatif; dans ce cas, des informations supplémentaires seraient obtenues pour savoir si le coefficient sous-estime ou surestime le paramètre de fiabilité simulé., À la suite de la recommandation de Hoogland et Boomsma (1998), les valeurs de RMSE < 0,05 et de biais en % < 5% ont été jugées acceptables.
Résultats
Les principaux résultats peuvent être vus dans le Tableau 1 (6 points) et le Tableau 2 (12 points). Ceux-ci montrent le biais RMSE et % des coefficients dans les conditions d’équivalence tau et congénères, et comment l’asymétrie de la distribution de test augmente avec l’incorporation progressive d’éléments asymétriques.
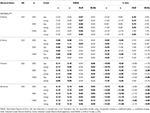
le Tableau 1., RMSE et biais avec équivalence tau et condition congénitale pour 6 éléments, trois tailles d’échantillon et le nombre d’éléments asymétriques.
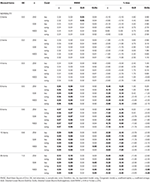
le Tableau 2. RMSE et biais avec équivalence tau et condition congénitale pour 12 éléments, trois tailles d’échantillon et le nombre d’éléments asymétriques.
seulement dans des conditions d’équivalence tau et de normalité (asymétrie< 0.2), on observe que le coefficient α estime correctement la fiabilité simulée, comme ω., Dans l’état congénère ω corrige la sous-estimation de α. Le GLB et le GLBa présentent tous deux un biais positif sous normalité, mais le GLBA présente un biais d’environ ½ % de moins que le GLB (voir le tableau 1). Si nous considérons la taille de l’échantillon, nous observons que lorsque la taille du test augmente, le biais positif du GLB et du GLBa diminue, mais ne disparaît jamais.
dans des conditions asymétriques, nous voyons dans le tableau 1 Que α Et ω présentent une performance inacceptable avec des RMSE croissants et des sous-estimations pouvant atteindre un biais > 13% pour le coefficient α (entre 1 et 2% inférieur pour ω)., Les coefficients GLB et GLBa présentent un RMSE inférieur lorsque l’asymétrie du test ou le nombre d’éléments asymétriques augmente (Voir tableaux 1, 2). Le coefficient GLB présente de meilleures estimations lorsque la valeur d’asymétrie du test est d’environ 0,30; GLBa est très similaire, présentant de meilleures estimations que ω Avec une valeur d’asymétrie du test d’environ 0,20 ou 0,30. Cependant, lorsque la valeur d’asymétrie augmente à 0,50 ou 0,60, GLB présente de meilleures performances que GLBa. La taille du test (6 ou 12 ítems) a un effet beaucoup plus important que la taille de l’échantillon sur l’exactitude des estimations.,
Discussion
dans cette étude, quatre facteurs ont été manipulés: l’équivalence Tau ou le modèle congénère, la taille de l’échantillon (250, 500 et 1000), le nombre d’items d’essai (6 et 12) et le nombre d’items asymétriques (de 0 items asymétriques à tous les items asymétriques) afin d’évaluer la robustesse à la présence de données asymétriques dans les quatre coefficients de fiabilité analysés. Ces résultats sont discutés ci-dessous.,
dans des conditions d’équivalence tau, les coefficients α Et ω convergent, mais en l’absence d’équivalence Tau (congénère), ω présente toujours de meilleures estimations et un biais RMSE et % plus petit que α. Dans cette condition plus réaliste donc (Green et Yang, 2009a; Yang et Green, 2011), α devient un estimateur de fiabilité biaisé négativement (Graham, 2006; Sijtsma, 2009; Cho et Kim, 2015) et ω est toujours préférable à α (Dunn et al., 2014). En cas de non-violation de l’hypothèse de normalité, ω est le meilleur estimateur de tous les coefficients évalués (Revelle et Zinbarg, 2009).,
en ce qui concerne la taille de l’échantillon, nous observons que ce facteur a un faible effet sous normalité ou un léger écart par rapport à la normalité: le RMSE et le biais diminuent à mesure que la taille de l’échantillon augmente. Néanmoins, on peut dire que pour ces deux coefficients, avec une taille d’échantillon de 250 et une normalité, nous obtenons des estimations relativement précises (Tang et Cui, 2012; Javali et al., 2011)., Pour les coefficients GLB et GLBa, à mesure que la taille de l’échantillon augmente, le RMSE et le biais tendent à diminuer; cependant, ils maintiennent un biais positif pour la condition de normalité même avec des échantillons de grande taille de 1000 (Shapiro et ten Berge, 2000; ten Berge et Sočan, 2004; Sijtsma, 2009).
pour la taille du test, nous observons généralement un RMSE et un biais plus élevés avec 6 items qu’avec 12, ce qui suggère que plus le nombre d’items est élevé, plus le RMSE et le biais des estimateurs sont faibles (Cortina, 1993). En général, la tendance est maintenue pour 6 et 12 éléments.,
lorsque nous examinons l’effet de l’incorporation progressive d’éléments asymétriques dans l’ensemble de données, nous observons que le coefficient α est très sensible aux éléments asymétriques; ces résultats sont similaires à ceux trouvés par Sheng et Sheng (2012) et Green et Yang (2009b). Le Coefficient ω présente des valeurs RMSE et polarisées similaires à celles de α, mais légèrement meilleures, même avec l’équivalence tau. GLB et GLBa présentent de meilleures estimations lorsque l’asymétrie du test s’écarte de valeurs proches de 0.
considérant qu’en pratique, il est courant de trouver des données asymétriques (Micceri, 1989; Norton et al.,, 2013; Ho et Yu, 2014), la suggestion de Sijtsma (2009) d’utiliser GLB comme estimateur de fiabilité semble fondée. D’autres auteurs, tels que Revelle et Zinbarg (2009) et Green et Yang (2009a), recommandent l’utilisation de ω, mais ce coefficient n’a produit de bons résultats qu’en condition de normalité ou avec une faible proportion d’éléments d’asymétrie. Dans tous les cas, ces coefficients présentaient des avantages théoriques et empiriques plus importants que α. Néanmoins, nous recommandons aux chercheurs d’étudier non seulement les estimations ponctuelles, mais aussi d’utiliser l’estimation par intervalles (Dunn et al., 2014).,
ces résultats sont limités aux conditions simulées et on suppose qu’il n’y a pas de corrélation entre les erreurs. Cela rendrait nécessaire de poursuivre les recherches pour évaluer le fonctionnement des différents coefficients de fiabilité avec des structures multidimensionnelles plus complexes (Reise, 2012; Green et Yang, 2015) et en présence de données ordinales et/ou catégorielles dans lesquelles le non-respect de l’hypothèse de normalité est la norme.
Conclusion
lorsque les résultats totaux des tests sont normalement distribués (c.-à-d.,, tous les éléments sont normalement distribués) ω devrait être le premier choix, suivi de α, car ils évitent les problèmes de surestimation présentés par GLB. Cependant, lorsqu’il y a une asymétrie d’essai faible ou modérée, le GLBa doit être utilisé. Le GLB est recommandé lorsque la proportion d’éléments asymétriques est élevée, car dans ces conditions, l’utilisation de α Et ω comme estimateurs de fiabilité n’est pas recommandée, quelle que soit la taille de l’échantillon.
Contributions des auteurs
développement de l’idée de recherche et cadre théorique (IT, JA). Construction du cadre méthodologique (IT, JA)., Développement de la syntaxe du langage R (IT, JA). Analyse et interprétation des données (IT, JA). Discussion des résultats à la lumière du contexte théorique actuel (JA, IT). Préparation et rédaction de l’article (JA, IT). En général, les deux auteurs ont également contribué au développement de ce travail.,
Financement
le premier auteur a déclaré avoir reçu le soutien financier suivant pour la recherche, la paternité et / ou la publication de cet article: il a reçu le soutien financier du programme de bourses de doctorat « Becas Chile” De La Commission nationale chilienne pour la recherche scientifique et technologique (CONICYT) (subvention No: 72140548).
déclaration de conflit d’intérêts
Les auteurs déclarent que la recherche a été menée en l’absence de toute relation commerciale ou financière pouvant être interprétée comme un conflit d’intérêts potentiel.
Cronbach, L. (1951)., Coefficient alpha et la structure interne des tests. Psychometrika 16, 297-334. doi: 10.1007/BF02310555
CrossRef Texte Intégral | Google Scholar
McDonald, R. (1999). Théorie du Test: un traitement unifié. Mahwah, NJ: Lawrence Erlbaum Associates.
Google Scholar
R Équipe de base de développement (2013). R: un langage et un environnement pour L’Informatique statistique. Vienne: Fondation R pour L’Informatique statistique.
Raykov, T. (1997)., Scale reliability, cronbach »s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package « psych.,” Disponible en ligne à: http://org/r/psych-manual.pdf
Shapiro, A., et dix Berge, J. M. F. (2000). Le biais asymptotique de l’analyse minimale du facteur trace, avec des applications à la plus grande limite inférieure de fiabilité. Psychometrika 65, 413-425. doi: 10.1007/BF02296154
CrossRef Texte Intégral | Google Scholar
à dix Berge, J. M. F., et Sočan, G. (2004). La plus grande limite inférieure à la fiabilité d’un test et à l’hypothèse d’unidimensionnalité. Psychometrika 69, 613-625. doi: 10.,1007/BF02289858
CrossRef Texte Intégral | Google Scholar
Woodhouse, B., et Jackson, P. H. (1977). Limites inférieures pour la fiabilité du score total sur un test composé d’éléments non homogènes: II: une procédure de recherche pour localiser la limite inférieure la plus élevée. Psychometrika 42, 579-591. doi: 10.1007/BF02295980
CrossRef Full Text/Google Scholar
annexe I
syntaxe R pour estimer les coefficients de fiabilité à partir des matrices de corrélation de Pearson., Les valeurs de corrélation en dehors de la diagonale sont calculées en multipliant la charge factorielle des éléments: (1) modèle équivalent tau ils sont tous égaux à 0,3114 (λiλj = 0,558 × 0,558 = 0,3114) et (2) Modèle congénère ils varient en fonction de la charge factorielle différente (par exemple, l’élément de matrice a1, 2 = λ1λ2 = 0,3 × 0,4 = 0,12). Dans les deux exemples, la fiabilité réelle est de 0,731.
> omega(Cr,1)$alpha # normalisé de Cronbach »s α
0.731
> omega(Cr,1)$omega.tot # coefficient ω total
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach »s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731