피타고라스는”정리

피타고라스가

통해 2000 년 전에 있었는 놀라운 발견에 대해 삼각형

때 삼각형은 바로 angle(90°)…<피>… 그리고 사각형은 각각의삼면,…<피>… 그런 다음 가장 큰 사각형은 다른 두 사각형을 함께 넣은 것과 똑같은 면적을 가지고 있습니다!,

그것은”피타고라스는”정리”와 작성할 수 있습에서 하나 짧은 방정식:

a2+b2=c2

참고:

• c 은 측 삼각형
• a 와 b 는 다른 두 개의 측

정의

가장 긴쪽의 삼각형이라”빗변이”,이렇게 공식적인 정의가:

확실합니다… ?예제를 사용하여 실제로 작동하는지 확인하십시오. 이것이 유용 할 수있는 이유는 무엇입니까?

직각 삼각형의 두 변의 길이를 알고 있다면 세 번째 변의 길이를 찾을 수 있습니다. (그러나 직각 삼각형에서만 작동한다는 것을 기억하십시오!)

어떻게 사용합니까?,

그것을 아래로 작성 방정식:

그리고 우리가 사용하는 대수를 찾을 수 없는 값으로 이러한 예제:

읽을 수도 있습에 대한 사각형과 사각형 뿌리는 이유를 알아√169=13

그것은 다른 방법으로,주위에도:을 때의 세 가지 측면은 삼각형을 a2+b2=c2,다음 삼각형은 바로 비스듬합니다.,

그리고 당신은 정리를 스스로 증명할 수 있습니다!

Get 종이와 펜 가위,다음 사용하여 다음과 같은 애니메이션으로 가이드:

• 그리른 각도에 삼각형의 종이,떠나는 공간을 많이합니다.,
• 그리 광장을 따라 사변(가장 긴쪽)
• 그리는 같은 크기의 광장에서 다른 쪽의 빗변
• 그리 라인에 표시 애니메이션,다음과 같다:
• 
• 잘라 모양
• 도록 그들을 정렬할 수 있음을 증명할 수 있습니다 큰 광장과 같은 지역의 두 광장에서 다른 측

,다른 놀랍게도,간단한 증명

여기에 가장 오래된 중 하나는 증거는 광장에서 긴쪽과 같은 지역에 다른 사각형입니다.,

애니메이션을보고 삼각형이 주위를 미끄러지기 시작할 때주의를 기울이십시오. 무슨 일이 일어나고 있는지 이해하기 위해 애니메이션을 몇 번보고 싶을 수도 있습니다.

보라색 삼각형이 중요한 것입니다.

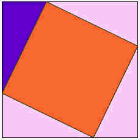된다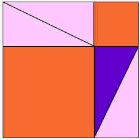