8.1 역사적인 예를 들어
그의 책에서,두 개의 새로운 과학,갈릴레오 갈릴레 Galilea(1564-1642)는 여러 논쟁을 보여주기 위한 것이 있을 수 없다는 것 같은 것은 실제 무한대 또는 실제 infinitesimals 주. 그의 주장 중 하나는 다음과 같은 방법으로 재구성 될 수있다. 갈릴레오 갈릴레이 제안하는 것은 우리가 전제로 거기에 실제 무한대의 자연수(자연의 숫자는 긍정적인 전체에서 번호 1):
{1, 2, 3, 4, 5, 6, 7, ….,}
그는 또한 제안 우리가 전제로가 있는 실제의 무한대의 자연의 숫자입니다.피>{1, 4, 9, 16, 25, 36, 49, ….}
이 갈릴레오 갈릴레이는 이유로 이러한 두 그룹(오늘 우리가 부르는”설정”)크기가 같습니다. 왜냐하면 두 그룹간에 일대일 대응이 있다는 것을 알 수 있기 때문입니다.,
| {1, | 2, | 3, | 4, | 5, | 6, | 7, ….,div> | |
| {1, | 4, | 9, | 16, | 25, | 36, | 49,…} |
경우 우리는 연결할 수 있는 모든 자연의 번호와 하나만장 번호,그리고 우리는 연결할 수 있습니다 모든 스퀘어 번호와 하나만 자연수,이러한 세트는 같은 크기여야 합니다.,그러나 잠시 기다려라,갈릴레오는 말한다. 분명히 정사각형 숫자가있는 것보다 매우 많은 자연수가 있습니다. 즉,모든 제곱 수는 자연수 목록에 있지만 자연수의 대부분은 제곱 수 목록에 없습니다. 다음 숫자는 모두 자연수 목록에 있지만 사각형 숫자 목록에는 없습니다.피>{2, 3, 5, 6, 7, 8, 10, ….,}
이 갈릴레오 갈릴레이는 이유가 있는 경우 많은 숫자를 그룹에서의 자연적인 숫자에 없는 그룹의 광장 번호,그리고 없는 경우에는 숫자를 그룹에서의 사각지 않은 숫자에서 원주민번호,다음을 자연의 숫자보다 큰 광장 번호. 그리고 자연수의 그룹이 제곱 숫자의 그룹보다 크면 자연수와 제곱 숫자는 같은 크기가 아닙니다.,
우리는 두 가지 결론에 도달했:설정은 자연의 숫자와의 설정이 광장 숫자는 같은 크기;그리고,설정은 자연의 숫자와의 설정이 광장 번호를 동일하지 않은 크기입니다. 그것은 모순입니다.
갈릴레오는 우리가 모순에 도달 한 이유는 우리가 실제 무한성이 있다고 가정했기 때문이라고 주장한다. 그러므로 그는 실제적인 무한함이 없다고 결론 지었다.
8.2 간접 증명
우리의 논리는 아직 유효한 인수를 증명할 정도로 강하지 않습니다. 다음 인수를 예로 들어 보겠습니다.,
(P→(QvR))
Q
R
P
이 인수를 보이는 유효합니다. 우리가 알고있는 첫 번째 전제로:P 가 사실이라면,그렇다면(Q v R)사실이 될 것입니다. 그러나 Q 또는 R 또는 둘 다 사실 일 것입니다. 그리고 두 번째와 세 번째 구내에 의해 우리는 알고 있습니다:Q 는 거짓이고 R 은 거짓입니다. 그래서 그것은(Q v R)true 일 수 없으므로 P 가 true 일 수는 없습니다.
진리표를 사용하여 인수를 확인할 수 있습니다. 우리의 전제 중 하나가 복잡하기 때문에 우리의 테이블은 복잡 할 것입니다.,
In any kind of situation in which all the premises are true, the conclusion is true., 즉,전제는 모두 마지막 행에서만 사실입니다. 그 행의 경우 결론도 마찬가지입니다. 그래서,이것은 유효한 인수입니다.그러나 잠시 시간을내어이 주장을 증명하려고합니다. 우리가 시작

그리고 지금 우리는 중지되었습니다. 우리는 우리의 규칙 중 하나를 적용 할 수 없습니다. 여기에 우리가 추론 시스템을 증명할 정도로 강하게 만들지 않은 유효한 논쟁이 있습니다.
이 문제를 바로 잡고 우리의 추론 시스템을 충분히 강하게 만드는 몇 가지 방법이 있습니다., 가장 오래된 중 하나는 솔루션을 소개하는 새로운 증거 방법은,전통적으로”이라는본주의 absurdum”,을 의미하는 감소하는 부조리이다. 이 방법은 종종”간접 증명”또는”간접 파생”이라고도합니다.결론에 대한 거부를 가정하고 모순이 발생한다는 것을 보여주는 것입니다. 우리가 어떤 문장 Ψ 과 그 부정 Ψ 을 증명할 때 모순이 나타납니다. 이것은 어떤 문장이든 가능합니다. 요점은,쌍발성의 원리가 주어지면,우리는 거짓된 것을 입증 했음에 틀림 없다는 것입니다. Ψ 가 참이면 Ψ 가 거짓이고 Ψ 가 참이면 Ψ 가 거짓입니다., 우리는 어느 것이 거짓인지 알 필요가 없습니다(Ψ 또는 Ψ);그 중 하나가 있어야한다는 것을 알기에 충분합니다.
우리는 진정한 진술에서 거짓을 생성 할 수 없도록 논리 시스템을 구축했음을 기억하십시오. 그러므로 우리가 간접적 인 파생에서 생산하는 거짓의 근원은 우리가 우리의 주장에 추가 한 몇 가지 거짓이어야합니다. 그리고 우리가 우리의 주장에 추가 한 것은 결론의 거부입니다. 따라서 결론은 사실이어야합니다.,
모양의 인수에는 다음과 같습니다:

전통적으로,가정에 대한 간접적인 파생되었 일반적으로”이라고 가정 대본주”.
구체적인 예로서,우리는 우리의 난처한 사건을 증명할 수 있습니다.

우리는 가정부의 결론에서 선 4. 우리가 옳다고 믿었던 결론은 P 였고,이것의 거부는 P 입니다.7 행에서 우리는 R 을 증명했습니다., 기술적으로,우리는 그 시점에서 수행하지만,우리에게 친절하려고 노력하는 사람을 이해의 방지,그래서 우리는 반복 line3 도록 문장의 R R 는 측면에서,그리고 그것은 매우 쉽게 무언가 잘못되었습니다. 즉,우리가 R 과 R 을 모두 입증했다면,우리는 거짓된 것을 입증했습니다.
우리의 추론은 이제 다음과 같이 진행됩니다. 무엇이 잘못 되었습니까? 라인 8 반복의 올바른 사용이다;라인 7 잠정 tollendo ponens 의 올바른 사용에서 온다;라인 6 잠정 ponens 의 올바른 사용에서;라인 5 이중 부정의 올바른 사용에서., 그래서 우리는 우리의 추론에 실수를하지 않았습니다. 우리는 1,2 및 3 행을 사용했지만,그것들은 우리가 정확하다고 가정하기로 동의 한 전제입니다. 이것은 4 줄을 남깁니다. 그것이 내 모순의 근원이되어야합니다. 그것은 거짓이어야합니다. 4 행이 false 인 경우 P 는 true 입니다.
어떤 사람들은 간접 증명이 직접 증명보다 덜 강하다고 생각합니다. 이것에 대한 많은,그리고 복잡한 이유가 있습니다. 그러나 우리의 명제 논리에 대해서는 이러한 이유 중 어느 것도 적용되지 않습니다. 왜냐하면 우리의 명제 논리가 일치한다는 것을 증명할 수 있기 때문입니다., 즉,먼저 시스템에 거짓을 도입하지 않으면 우리의 명제 논리가 거짓을 증명할 수 없다는 것을 증명할 수 있습니다. (일반적으로 이러한 시스템 내부에서보다 강력하고 진보 된 논리 또는 수학적 시스템이 일관성이 있음을 증명할 수는 없습니다. 여)할 수 있다는 것을 특정의의 일관성을 명제 논리,우리가 할 수 있습에서 우리의 명제 논리는 간접적인 증거가 좋은 형태의 추론이다., 우리가 알고 있는 경우에 우리는 증명하기 위해 거짓말,우리는 넣어 가지고 거짓을 경우 우리는 자신감에 대한 다른 모든 가정을(즉,프)우리 증거를 제외한 가정을 위한 간접적인 유도 있습니다,그 후에 우리는 자신감이 가정에 대한 간접적인 유도해야 하는 소스의 거짓말.
여기에 용어에 대한 메모가 필요합니다. “모순”이라는 단어는 대부분의 논리 토론에서 모호하게 사용됩니다. 그것은 두 문장이 주장되는 위에서 보는 것과 같은 상황을 의미 할 수 있으며,이 문장은 모두 사실 일 수 없습니다., 또는 사실 일 수없는 단일 문장을 의미 할 수도 있습니다. 그러한 문장의 예는(P^P)입니다., 진리 테이블을 위해 이 문장입니다:
| P | P | (P^P) |
|---|---|---|
| T | F | F |
| F | T | F |
이에 따라,이런 종류의 문장이 현실이 되지 않에 관계없이 의미의 P.,
혼란을 피하기 위해 이 텍스트에서,우리는 항상 통화를 하나의 문장될 수 없는 진정한”모순되는 문장”. 따라서(P^P)는 모순 된 문장입니다. 둘 다 사실 일 수없는 두 문장이 주장되는 상황은”모순”이라고 불릴 것입니다.
8.3 우리의 예와 다른 예
우리는 지금 갈릴레오의 논증의 버전을 재구성 할 수 있습니다. 우리는 다음 키를 사용할 것입니다.
P:실제 무한대(자연수와 제곱수 포함)가 있습니다.,
Q:자연수와 제곱수 사이에는 일대일 대응이 있습니다.자연수 집합의 크기와 제곱수 집합의 크기는 동일합니다.
S:모든 제곱 숫자는 자연수입니다.
T:자연수 중 일부는 정사각형 숫자가 아닙니다.
U:정사각형 숫자보다 자연수가 더 많습니다.,
이 핵심,인수 번역됩니다:
(P→Q)
(Q→R)
(P→(S^T))
((S^T)→U)
(U→R)
P
그리고 우리는 증명이 유효한 인수를 사용하여 간접적인 유도:

On line6,우리 가정 P 기 때문에 믿고 갈릴레오 갈릴레이는 P 고 목적을 증명하는 P. 는 것은,그가 믿고 없는지 실제 무한대, 그래서 가정이 그것이 거짓을 하는 것을 믿지 않는 경우가 있지 않은 실제 무한대. 이 거짓은 그 자체를 드러내는 다른 거짓으로 이어질 것입니다.,
관심있는 사람들을 위해:갈릴레오는 실제 무한대는 없지만 잠재적 인 무한대가 있다고 결론지었습니다. 따라서,그가 권하지 않는 경우는 모든 자연적인 존재하는 숫자를(어떤 의미에서의”존재”),하지만 그것은 사실 당신을 셀 수 없이 자연수원합니다. 많은 철학자하기 전과 후에는 갈릴레오 갈릴레이 개최 이 보기에,그것은 비슷한 뷰를 개최하여 아리스토텔레스,사람이었다 중요한 논리와 철학자를 쓰는 거의 두 천 년 전 갈릴레오.,이와 같은 논증에서 간접적 인 파생에 대한 가정이 아니라 오히려 전제 중 하나가 모순의 근원이라고 추론 할 수 있습니다. 오늘날 대부분의 수학자들은 갈릴레오의 주장에 대해 이것을 믿습니다. 에서 논리학과 수학자라는 게오르그 Cantor(1845-1918),발명자의 이론을 설정하는 무한한 설정할 수 있는 적절한 하위 집합의 동일한 크기입니다., 즉,칸토어 거부되는 전제 4 위에도 모든 제곱 번호는 자연의 숫자,그리고 모든 자연수는 광장 번호,이하지 않는 경우 이러한 두 집합은 서로 다른 크기입니다. Cantor 받아 그러나 전제로 2 위,그리고,따라서,믿의 크기가 설정한 자연의 번호와의 크기가 설정의 광장 숫자는 동일합니다. 오늘날 사용하여 칸토어의 논리,수학자와 논 연구의 무한대 및 에 의해 개발되었 큰 본문 지식에 대한 자연의한다. 관심이 있다면 17.5 절을 참조하십시오.,
간접 유도를 설명하기 위해 다른 예를 고려해 보겠습니다. 매우 유용한 정리 세트는 오늘날 논리학자인 Augustus De Morgan(1806-1871)이후”De Morgan’S Theorems”라고 불립니다. 우리는 이러한 상태까지 완전히 제 9 장,하지만 우리가 할 수 있는 상태에서의 해당 영어:DeMorgan 관찰(PvQ)및(P Q)은 해당하는,또는(P Q)및(PvQ)은 동일합니다. 이 점을 감안할 때((PvQ)→(P^Q))우리 언어의 정리 여야합니다. 이것을 증명합시다.
전체 수식은 조건부이므로 조건부 유도를 사용할 것입니다., 우리는 증거 해야 합 따라서 시작:
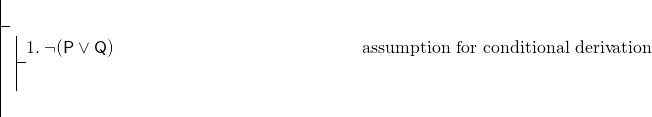
를 완료합 조건을 유도,우리는 증명해야 합니다(P Q). 이것은 결합이며,접속사를 보여주기위한 우리의 규칙은 가처분입니다. 이후 이 규칙을 사용하여 수 있습 우리의 가장 좋은 방법을 보여(P Q),우리가 할 수 있습을 표시하는 것을 목표로 P 쇼 Q,그리고 다음을 수행 adjunction. 그러나,우리는 분명히 작업 할 것이 거의 없습니다—단지 라인 1,이는 부정입니다. 이러한 경우 일반적으로 간접적 인 증거를 시도하는 것이 현명합니다. P 의 간접적 인 증거로 시작하십시오.,

우리는 지금을 찾을 필요가 모순 어떤 모순이다. 그러나 이미 명백한 것이 있습니다. 1 행은 P 도 Q 도 사실이 아니라고 말합니다. 그러나 라인 3 은 p 가 사실이라고 말합니다. 우리는 공식과 그 거부를 발견함으로써이 모순을 명시 적으로 만들어야합니다. 우리는 추가를 사용하여 이것을 할 수있다.

을 완료하는 증거,우리가 사용하는 이 전략을 다시합니다.

우리는 De Morgan 의 정리를 9 장의 문제로 증명할 것입니다.,
여기에 일반적인 엄지손가락의 규칙을 하기를 위한 증명을 때 증명하는 조건으로 항상 유도 조건,그렇지 않으면 시도 직접적인 유도;실패하는 경우 다음을 시도,간접는 상속할 수 없습니다.
8.4 문제
- 다음 증명을 완료하십시오. 각각은 간접적 인 파생이 필요합니다. 마지막 두 가지는 도전적입니다.
- 다음은 정리임을 증명합니다.
- (P^P).
- ((P→P)^(P→P)).
- (P→(P^Q)).
- ((P^Q)→(P→Q)).
- 일반 구어체 영어에서는 적어도 두 개의 전제로 자신의 유효한 인수를 작성하십시오., 당신의 주장은 단지 단락이어야합니다(문장의 정렬 된 목록이나 형식 논리처럼 보이는 다른 것이 아닙니다). 그것을 명제 논리로 번역하고 간접 파생을 사용하여 유효하다는 것을 증명하십시오.
이 번역문은 제목의 갈릴레오 갈릴레의 책은 가장 일반적 있지만,더 문자는 수학적 담론을 전수받게 된다. 이 책의 번역본에는 드레이크(1974)가 포함됩니다.