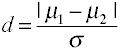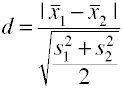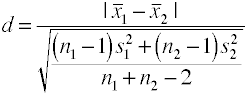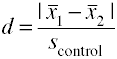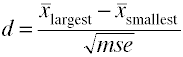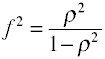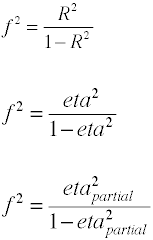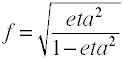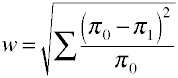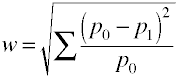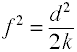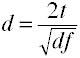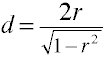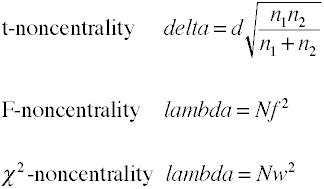중 하나를 사용의 효과로 표준화된 인덱스의 독립적인 샘플 크기 및 수량화하의 크기 사이의 차이를 인구 또는 사이의 관계를 설명하고 응답을 변수입니다. 효과 크기의 또 다른 용도는 수행에 사용됩니다전원 분석.
효과 크기를 위한 의미의 차이
효과에 대한 크기의 차이에 의미가 주어진 byCohen d 에서 정의된 측면의 인구단(µs)인구 편차(σ),은 아래와 같습니다.,
있는 여러 가지 다른 방법으로 추정 할 수 있습 σ 에서 샘플 데이터 whichleads 여러 개에서 코헨의 d 다.
를 사용하여 제곱 평균 표준 편차
를 사용하여 풀 표준편차(스’g)
이전 버전의 코헨의 d 사용하여 풀 표준 편차도 알려져 있으로 울타리’g.,
얻을 수 있습니다 쉽게 이 값을 분산 분석 프로그램을 복용하여 사각형 뿌리의 meansquare 오류가 있는 것으로도 알려져 있 root mean square 오류가 있습니다.
대조군 표준 편차 사용(Glass’Δ)
대조군에 대한 표준 편차를 사용하는 Cohen 의 d 의 또 다른 버전은 glass’Δ 라고도합니다.,
더 많은 다음 두 그룹
더 있을 때 다음 두 그룹 사이에 차이는 가장 큰 및 smallestmeans 어 루트의 평균 오류가 있습니다.
효과 크기는 F-비율에서 회귀분석
을 위해 OLS 회귀를 측정하는 효과의 크기는 F 에 의해 정의되는 코헨 다음과 같습니다.,
다시 한 번 여러 가지 방법이 있는 효과 크기를 계산할 수 있습에서 샘플 데이터를 확보합니다. Notethat η2 는 R2 의 또 다른 이름입니다.
효과 크기는 F-비율에 분산분석
효과 크기에 사용되는 분석의 차이에 의해 정의의 비율 인구 standarddeviations.,
지만 코헨 f 은 위와 같이 정의 그것은 일반적으로 computedby 의 제곱근을 취하 f2.
효과 크기를 위한 χ2 에 대비한 테이블
다시 한번 우리가 시작하는 명확한 공식 인구의 측면에서 값입니다.효과 크기 w 는 표준화 된 카이 제곱 통계의 제곱근입니다.,
그리고 여기에는 방법이 사용하여 계산된 샘플 데이터를 확보합니다.
여기에의 테이블에 대한 제안된 값 저,중,고 효과(코헨,1988). 이 값들은 절대자로 간주되어서는 안되며 연구 프로그램의 맥락에서 해석되어야합니다. Forlarge 효과 값은 코헨의 d 가 1.0 보다 큰 값이 드물지 않아 실제로 자주 초과됩니다.,그러나 사용하여 매우 큰 효과 크기에서 잠재력을 분석은 좋은 생각이너로 이어질 수 있에서 전원 연구이다.,식
치 k=숫자의 그룹
변환 t d 에 대한 두 개의 독립 그룹
변환 r d 에 대한 두 개의 독립 그룹
Noncentrality 추정
전력 분석을 사용하여 분석 방법을 필요로 예상 noncentrality 는 basicallythe 효과 크기를 곱해 샘플 크기는 요인이다., 다음은 비중심을 추정하기위한 몇 가지 공식입니다.
예력 분석
여기에 예를 함께 제공하는 효과 크기와 noncentrality 에 힘을 분석합니다.
세 그룹(k=3)을 가진 분산의 단방향 분석을 고려하십시오. 우리가 andeta2 가 같을 것으로 기대한다면.,12 는 경우에 효과는 크기가 될 것입니다
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
으로 예상된 샘플 크기의 60 의 추정 noncentrality
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
분자 자유도는 k-1=3-1=2 분모 df N-k=60-3=57.2 및 57 자유도를 갖는 F 의 임계 값은 3.16 입니다. 따라서,60 의 n 및 효과 크기의
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
의 힘을 초래한다.369 는 약 예상 전력을 산출합니다.7.
우리는의 힘에 개량해서 좋습니다.7 60 대신 75 의 투영 샘플 크기를 사용하여., 의 동일한 효과 크기로.369,우리는
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
분모 자유도는 동일하게 유지되는 반면 분모 df 는 이제 n-k=75-3=72 와 같습니다.2 및 72 자유도의 f 의 임계 값 3.12. 이 때 힘은
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
허용 가능한 연구 한계 내에 있습니다.
참고는 다른 통계 패키지를 사용하여 다른 이름과 다른 순서의 인수에는 함수가 호출 noncentralFtail. 설명서를 읽어야합니다.귀하의 소프트웨어와 함께.,
Becker,L.Psychology590 코스 노트. 볼 19Jun2009 년<http://web.uccs.edu/lbecker/Psy590/es.htm>
코헨,J.1988. 행동 과학에 대한 통계적 힘 분석. Hillsdale,New Jersey:Lawrence Erlbaum Associates