α 계수가 가장 널리 사용되는 절차에 대한 추 신뢰성에 적용되는 연구이다. 에 의해 명시된 바와 같 Sijtsma(2009),그 인기는 cronbach 의(1951)로 인용되었 참조보다 더 자주에서 문서 검색 DNA 의 두 번 나선., 그럼에도 불구하고,그것의 제한 잘 알려져 있(주고 노빅은,1968 년;Cortina,1993;양과 녹색,2011),몇몇을의 가장 중요한 가정의 상관 관계가 없는 오류를 tau-동등성 및상이 아니다.
가정의 상관 관계가 없는 오류를(에 오류가 점수의 모든 쌍의 항목은 상관되지 않은)가설적인 테스트론(주고 노빅,1968),을 위반할 수 있는 존재를 의미의 복잡한 다차원 구조를 필요로 추정한 절차는 이러한 복잡성을 계정으로(예를 들어,Tarkkonen 및 Vehkalahti,2005;녹색과 양,2015)., 눈금이 단차원이라면 그 값이 더 높을 것이기 때문에 α 계수가 단차원의 좋은 지표라는 잘못된 믿음을 뿌리 뽑는 것이 중요합니다. 실제로 정반대의 경우는 Sijtsma(2009)에 의해 보여 지듯이 그러한 조건에서의 적용은 신뢰성이 크게 과대 평가 될 수있다(Raykov,2001). 결과적으로 α 를 계산하기 전에 데이터가 단차원 모델에 맞는지 확인해야합니다.
타우-동등성의 가정(즉,, 동일한 진정한 점수를 위해 모든 테스트 항목,또는 동등한 요인은 선적의 모든 항목에서 계승 모델)의 요구 사항에 대한 α 동등하다고 신뢰성 계수(cronbach 의,1951). 면 가정의 tau-동등성을 위반하는 진정한 신뢰성 값이 과소 평가(Raykov,1997;그레이엄,2006 년)에 의하여 양에 따라 달라질 수 있습니다 간 0.6 11.1%의 심각성에 따라 위반(녹색과 양,2009a). 이 가정을 준수하는 데이터로 작업하는 것은 일반적으로 실제로 실행 가능하지 않습니다(teo and Fan,2013).,,다른 요인 적재)는 더 현실적입니다.
요구 사항에 대한 다중 변형 정상적 덜 알려진 모두에 영향을 미칩 puntual 신뢰성 추정과의 가능성에 대한 신뢰를 구축하는 데 간격(던 et al., 2014). 모리고 모리(2012)관찰 최근에는 그 때의 배포판은 비뚤어 및/또는 leptokurtic,부정적인 편견을 생산 계수 α 계산;유사한 결과를 제출되었으로 녹색과 양(2009b)분석에서의 효과의 정규분포 추정에 신뢰성입니다., 왜곡 문제에 대한 연구는 실제로 연구자들이 습관적으로 기울어 진 비늘로 작업하는 것을 볼 때 더 중요합니다(Micceri,1989;Norton et al.,2013;호와 유,2014). 예를 들어,Micceri(1989)으로 추정된 약 2/3 의 능력과 4/5 이상의 심리 조치 전시에서 적어도 중간 비대칭(즉,왜도 1). 그럼에도 불구하고,신뢰성 추정에 대한 왜도의 영향은 거의 연구되지 않았다.,
을 고려한 풍부한 문학에 대한 제한 사항과 편견의 α 계수(리벨’은 부유해요 및 Zinbarg,2009;Sijtsma,2009 년,2012 년;Cho 및 Kim,2015 년;Sijtsma 및 van der Ark,2015)은 문제가 발생,유로 연구를 계속 사용 α 때 대체수가 존재하는 극복한 이러한 제한이 있습니다. 지난 세기에 개발 된 신뢰성을 추정하기위한 절차의 초과가 논쟁을 불러 일으켰을 가능성이 있습니다. 이것은이 계수를 계산하는 단순성과 상업용 소프트웨어에서의 가용성에 의해 더욱 악화되었을 것입니다.,
의 어려움을 추정하 pxx 의 신뢰성 계수에 있는 그것의 정의 pxx’=σt2∕σx2 포함하는 진정한 점수에 분산 분자 할 때 이것은 자연에 의해 관측. Α 계수는 항목 또는 구성 요소 간의 공분산에서이 측정 할 수없는 분산을 근사하려고 시도합니다. Cronbach(1951)는 tau-등가가없는 경우 α 계수(또는 α 와 동등한 Guttman”s lambda3)가 좋은 하한 근사치임을 보여 주었다., 따라서,가정을 위반하는 문제로 번역을 찾는 최고의 하;사실 이 이름은 주어진 가장 낮은 바인딩 방법(GLB)는 가능한 최상의 근사치의 이론 각도(잭슨 Agunwamba,1977;스와 잭슨,1977;Shapiro 및 ten berge 의,2000;Sočan,2000;ten berge 의고 Sočan,2004;Sijtsma,2009). 그러나 Revelle 과 Zinbarg(2009)는 ω 가 GLB 보다 더 나은 하한을 제공한다고 생각합니다., 그러므로 해결되지 않은 토론으로 하는 이러한 두 가지 방법을 제공하는 최고의 하;또한 질문의 비 정상되지 않은 철저하게 조사로서 현재 작업에 대해 설명합.
ω 계수
맥도날드(1999)제 wt 계수 추정을 위한 신뢰도에서 요인 분석에 프레임워크로 표현할 수 있으로 공식적으로.
어디 λj 로드의 항목 j,λj2 공통점의 항목 j 및 ψ 과 동일합니다., Wt 계수를 포함하여 람다에 수식은 모두에 적합한 경우 tau-동등성(즉,같은 요인이 부하의 모든 테스트 항목)이 존재하는지(중량과 일치하는 수학적으로 α),을 때의 항목과 다른 차별이 존재하는 표현에서의 구조(즉,다른 요인 적재 항목:congeneric 측정). 결과적으로 wt 는 타우-동등성의 가정이 위반 될 때 α 의 과소 평가 편향을 수정한다(Dunn et al.,2014)및 다른 연구 결과에 따르면 신뢰성을 추정하기위한 최선의 대안 중 하나입니다(Zinbarg et al.,,2005,2006;Revelle and Zinbarg,2009),현재까지 비뚤어 짐의 조건에서의 기능은 알려지지 않았지만.
경관 사이에 존재하는 오류를,또는 하나 이상의 잠재적 차원에서 데이터,이 기여는 각 차원을 총 분산 설명하는 예상을 얻는 계층적 ω(wh)할 수 있는 해결하기 위해 저희에게 최악의 편견을 과대 평가 α 다차원 데이터(참조하십시오 Tarkkonen 및 Vehkalahti,2005;Zinbarg et al. 그 결과,그 결과는 다음과 같습니다., 계수 wh 와 wt 는 단차원 데이터에서 동일하므로이 계수를 단순히 ω 로 참조 할 것입니다.
가장 낮은 바인딩(GLB)
Sijtsma(2009)에 보여줍 연구 시리즈 중의 하나는 가장 강력한 평가의 신뢰성은 GLB—으로 추론 스와 잭슨(1977)에서 가정의 클래식 테스트 이론(Cx=Ct+Ce)—간 품목 공분산 행렬에 대한 관찰된 항목 점수 Cx. 그것은 두 부분으로 나뉩니다:항목 true scores Ct 에 대한 항목 간 공분산 행렬의 합;및 항목 간 오류 공분산 행렬 Ce(ten Berge and Sočan,2004)., 그것의 표현입니다:
어디 σx2 테스트 분산 및 tr(Ce)는 추적의 항목 오류가 공분산 행렬는 그것을 입증했다 그래서 예측하기 어렵다. 하나의 솔루션은 사용하는 요인 설계 절차 등의 최소 순위 요인 분석(절차로 알려진 glb.파). 보다 최근에 Glb 대수(GLBa)절차는 Andreas Moltner(Moltner and Revelle,2015)가 고안 한 알고리즘에서 개발되었습니다., 에 따라 리벨’은 부유해요(2015a)이 절차를 채택하는 형태로 가장 원본에 충실하여 정 잭슨 Agunwamba(1977),그리고 그의 추가 장점이 있습을 소개하는 벡터 무게는 항목에 의해 중요성(Al-Homidan,2008).
에도 불구하고 그것의 이론적 강점,GLB 은 아주 작은 사용되지만,최근 경험적 연구 결과는 이 계수보다는 더 나은 결과를 α(Lila et al. 2014 년)및 α 및 ω(스 et al., 2014)., 그럼에도 불구하고,작은 샘플에서,가정에서는 정규성,그것이 과대 평가하는 진정한 신뢰성 가치(Shapiro 및 ten berge 의,2000);그러나 그 기능에서 비 정상적인 조건에 남아 있을 알 수없는,특히 때 배포판의 항목은 비대칭한다.
을 고려하수 위에서 정의,그리고 이 편견과 제한 각각의 물체의 작동을 평가하고 견고 이들의 계수를 존재 하에서의 비대칭 항목을 고려하고,또한 가정의 tau-동등성 및 샘플 크기입니다.,
방법
데이터 생성
데이터를 사용하여 생성된 R(R 개발의 핵심 팀,2013 년)및 RStudio(Racine,2012)소프트웨어,다음 계승 model:
어디 Xij 는 시뮬레이션 응답의 예에서 나는 항목 j,λjk 로드의 항목에서 계수 k(는 생성에 의해 unifactorial 모델);Fk 은 잠재 요소를 생성에 의해 정상적인 표준화된 유통(0 평균과 분산 1),고 ej 는 임의의 측정에 오류가의 각 품목 또한 다음과 같은 표준화 정상 유통.,
괴상품:표준 정규 Xij 변형되었을 생성하는 비 정상적인 사용하여 분포한 절차에 의해 제안 Headrick(2002)을 적용하는 다섯 번째 순서는 다항식을 변환합니다.
조건을 시뮬레이션
의 성능을 평가하는 신뢰성 계수(α,ω,GLB 및 GLBa) 우리와 함께 일 세 샘플 크기(250,500,1000),두 개의 테스 크기:단기(6 개품목)및 장(12 개 품목),두 가지 조건의 타우-동등성(중 하나로 tau-동일 하나 없이,즉,,선천적 인)및 비대칭 항목의 진보적 인 통합(모든 항목이 정상인 것에서 모든 항목이 비대칭 인 것까지). 에서 짧은 테스트를 신뢰도 설정에서 0.731 는 존재 하에서의 tau-동등성을 달성을 가진 여섯 개의 항목을 가진 요소 적재=0.558 는 congeneric 모델 얻을 설정하여 요인은 하중에서의 값 0.3, 0.4, 0.5, 0.6, 0.7, 과 0.8(부록 I). 12 개 항목의 긴 테스트에서 신뢰도는 0 으로 설정되었습니다.,845 동일한 값으로 짧은 테스트를 위한 모두 tau-동등성 및 congeneric 모델(이 경우에있는 두 개의 항목에 대한 각각의 가치한 람다). 이러한 방식으로 120 개의 조건이 각각의 경우에 1000 개의 복제본으로 시뮬레이션되었습니다.
데이터 분석
주요 분석은 α 와 ω 를 추정 할 수있는 Psych(Revelle,2015b)와 GPArotation(Bernaards and Jennrich,2015)패킷을 사용하여 수행되었습니다. Glb 를 추정하기 위해 두 가지 전산화 된 접근법이 사용되었습니다:glb.파(Revelle,2015a)및 glb.,대수(Moltner and Revelle,2015),후자는 Hunt and Bentler(2015)와 같은 저자가 작업했습니다.
신뢰성을 복구하는 데있어 다양한 추정기의 정확성을 평가하기 위해 루트 평균 오차 제곱(RMSE)과 바이어스를 계산했습니다. 첫 번째는 것을 의미의 차이점으로 예상 및 시뮬레이션된 신뢰성을 공식화로:
어디 ρ^는 예상된 신뢰성에 대한 각 계수,ρ 시뮬레이션 신뢰성 및 Nr 수의 복제본이 있습니다., 이%편견으로 이해하는 사이의 차이는 것을 의미의 예상된 신뢰성 및 시뮬레이션된 신뢰성을 다음과 같이 정의됩니다.
모두에서 지수,이 값이 클수록 더 큰 부정확성의 평가,그러나 달리 RMSE,바이어스 될 수 있습 긍정적 또는 부정적인; 이 경우에는 추가적인 정보 획득하는지 여부를 계수가 과소 평가 또는 평가 시뮬레이션된 신뢰성을 매개 변수입니다., 다음의 추천 않나요?및 Boomsma(1998)의 값을 RMSE<0.05%bias<5%었다 허용되는 것으로 간주됩니다.
결과
주요 결과는 표 1(6 항목)과 표 2(12 항목)에서 볼 수 있습니다. 이러한 표시 RMSE 고%편견의 계수 tau-동등성 및 congeneric 조건,그리고 어떻게 왜도의 테스트는 배포 증가로 점차적인 법인의 비대칭 항목입니다.
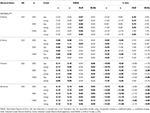
표 1., 6 개의 항목,3 개의 샘플 크기 및 왜곡 된 항목 수에 대한 타우 등가성 및 선천적 조건을 갖는 RMSE 및 바이어스.
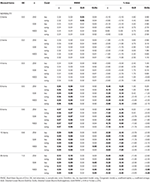
표 2. 12 개의 항목,3 개의 샘플 크기 및 왜곡 된 항목 수에 대한 타우-동등성 및 선천적 조건을 갖는 RMSE 및 바이어스.
만의 조건 하에서 tau-동일성과는 정(왜도<0.2)그것은 관찰되는 α 계수 추정 시뮬레이션된 신뢰성을 제대로,다음과 같 ω., 선천적 인 조건에서 ω 는 α 의 과소 평가를 수정합니다. GLB 와 GLBa 는 모두 정규성 하에서 양의 바이어스를 나타내지 만,GLBa 는 GLB 보다 근사하게½%적은 바이어스를 나타낸다(표 1 참조). 면 우리는 샘플 크기,우리가 관찰하는 테스트와 같은 크기가 증가함에 따라 긍정적인 편견의 GLB 및 GLBa 감소하고,그러나 결코 사라집니다.
에서 비대칭 조건에서,우리는 표 1 에서 모두 α 및 ω 제시 용납할 수 없는 성능을 증가와 함께 RMSE 및 underestimations 는 도달 할 수 있습니다 bias>13%에 대한 α 계수(1~2%정도 낮에 대한 ω)., GLB 및 GLBa 계수는 테스트 왜곡 또는 비대칭 항목 수가 증가 할 때 더 낮은 RMSE 를 나타냅니다(표 1,2 참조). GLB 계수 선물을 더 추정 테스트 왜도 값의 테스트는 주변에 0.30;GLBa 와 매우 유사시에는 더 나은 추정치 이상 ω 으로 테스트 왜도 값 주위 또는 0.30 0.20. 그러나 왜곡 값이 0.50 또는 0.60 으로 증가하면 GLB 는 GLBa 보다 우수한 성능을 나타냅니다. 시험 크기(6 개 또는 12 개의 데이텀)는 견적의 정확도에 대한 표본 크기보다 훨씬 중요한 영향을 미칩니다.,
토론
이 연구에서는 네 가지 요인이 조작:타우 동일하거나 congeneric 모델 샘플 크기(250,500,1000),숫자의 테스트 항목(6and12)의 수 및 비대칭품(비대칭 0 품목하는 모든 항목되는 비대칭)을 평가하기 위해 견고성의 존재에 비대칭 데이터에서는 네 개의 신뢰성 계수를 분석합니다. 이러한 결과는 아래에서 설명합니다.,
tau-등가 조건에서는 α 와 ω 계수가 수렴하지만 tau-등가(선천성)가없는 경우 ω 는 항상 α 보다 더 나은 추정치와 더 작은 RMSE 및%바이어스를 나타냅니다. 그러므로보다 현실적인 조건에서(Green and Yang,2009a;Yang and Green,2011),α 는 부정적으로 편향된 신뢰성 추정자(Graham,2006;Sijtsma,2009;Cho And Kim,2015)가되고 ω 는 항상 α 보다 바람직하다(Dunn et al., 2014). 정규성 가정을 위반하지 않는 경우 ω 는 평가 된 모든 계수의 최상의 추정기입니다(Revelle and Zinbarg,2009).,
선회하는 샘플 크기,우리가 관찰하는 요인은 작은 효과가에서 정상 또는 경미한 출발에서는 정규성:the RMSE 과 편견으로 축소 샘플 크기가 증가합니다. 그럼에도 불구하고,그것은 말할 수는을 위한 이러한 두 가지 계수 샘플 크기는 250 고 정상 우리는 비교적 정확한 견적(당나라와 Cui,2012;Javali et al., 2011)., 에 대한 GLB 및 GLBa 계수 샘플 크기가 증가 RMSE 과 편견하는 경향이 감소한다;그러나 그들은 긍정적인 편견에 대한 조건의 정상에도 큰 샘플 크기의 1000(Shapiro 및 ten berge 의,2000;ten berge 의고 Sočan,2004;Sijtsma,2009).
에 대한 테스트 크기는 일반적으로 관찰하는 더 높은 RMSE 과 편견으로 6 개 항목보다 12 것을 제안,높은 수의 항목,낮은 RMSE 과 편견의 추정기(Cortina,1993). 일반적으로 추세는 6 개 및 12 개 항목 모두에 대해 유지됩니다.,
볼 때 우리는 효과를 점차적으로 통합하는 비대칭 항목을 데이터로 설정을 관찰하는 α 계수가 매우 민감하는 비대칭 항목에 이러한 결과는 비슷하에 의해 발견되는 모리고 모리(2012)및 녹색과 양(2009b). 계수 ω 는 α 의 값과 유사한 RMSE 및 바이어스 값을 나타내지 만 tau-동등성으로도 약간 더 좋습니다. GLB 와 GLBa 는 테스트 왜도가 0 에 가까운 값에서 출발 할 때 더 나은 추정치를 제시하는 것으로 밝혀졌습니다.
실제로 비대칭 데이터를 찾는 것이 일반적이라는 점을 고려할 때(Micceri,1989;Norton et al.,,2013;Ho and Yu,2014),glb 를 신뢰성 추정기로 사용하는 Sijtsma 의 제안(2009)은 잘 설립 된 것으로 보입니다. 다른 저자가 같은 리벨’은 부유해요 및 Zinbarg(2009)그리고 녹색과 양(2009a),의 사용을 권장합 ω,그러나 이 계수만을 생산하는 좋은 결과의 상태에서는 정규성 또는 저렴한 비율의 왜도 항목입니다. 어쨌든,이러한 계수는 α 보다 더 큰 이론적 및 경험적 이점을 제시했다. 그럼에도 불구하고,우리는 지키는 추정뿐만 아니라 간격 추정의 사용을 만들기 위해 연구자를 권장합니다(Dunn et al., 2014).,
이러한 결과는 시뮬레이션 된 조건으로 제한되며 오류간에 상관 관계가 없다고 가정합니다. 이 것이 그것을 만들 수행하는 데 필요한 추가 연구를 평가하는 기능의 다양한 신뢰성 계수와 함께 더 복잡한 다차원 구조(Reise,2012;녹색과 양,2015)고의 존재에 서수 및/또는 범주형 데이터에서는 non-compliance with 가정의 정상이 표준입니다.
결론
총 시험 점수가 정상적으로 분배 될 때(즉,, glb 가 제시 한 과대 평가 문제를 피하기 때문에 모든 항목이 정상적으로 분배됩니다)ω 는 α 가 뒤 따르는 첫 번째 선택이어야합니다. 그러나,낮거나 중간 정도의 시험 왜곡 GLBa 가 사용되어야하는 경우. GLB 권장 비율의 비대칭 항목이 높고,이후 이러한 조건에서의 사용을 모두 α 및 ω 으로 신뢰도 평가 있는 것은 바람직하지 않 무엇이든 샘플 크기입니다.
저자 기여
연구 및 이론적 틀의 아이디어 개발(IT,JA). 방법 론적 틀의 건설(IT,JA)., R 언어 구문 개발(IT,JA). 데이터 분석 및 데이터 해석(IT,JA). 현재의 이론적 배경에 비추어 결과에 대한 토론(JA,IT). 기사 준비 및 작성(JA,IT). 일반적으로 두 저자 모두이 작품의 발전에 동등하게 기여했습니다.,
자금 지원
첫 번째 저자는 공개하의 영수증을 다음과 같은 재정 지원에 대한 연구,저작권 및/또는 게시 이 문서의:그로부터 재정 지원을 받는 칠레 국립 위원회에 대한 과학 기술 연구(CONICYT)”Becas 칠레는”박사 펠로우십 프로그램(권한을 부여 없:72140548).
이해의 충돌 문
저자가 선언하는 연구가 수행되었의 부재에서 어떠한 상업 또는 금융 서비스를 제공하는 것으로 해석될 수 있는 잠재적인 이해의 충돌.
Cronbach,L.(1951)., 계수 알파 및 테스트의 내부 구조. Psychometrika16,297-334. doi:10.1007/BF02310555
CrossRef 전체 텍스트|Google Scholar
McDonald,R.(1999). 시험 이론:통일 된 치료. 마화,뉴저지:로렌스 얼 바움 어소시에이츠.
Google Scholar
R 개발 핵심 팀(2013). R:통계 컴퓨팅을위한 언어 및 환경. 비엔나:통계 컴퓨팅을위한 R 재단.그 이유는 다음과 같습니다., Scale reliability, cronbach”s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package “psych.,”온라인에서 사용 가능:http://org/r/psych-manual.pdf
Shapiro,A.,and ten Berge,J.M.f.(2000). 신뢰성에 가장 큰 하한에 응용 프로그램과 함께 최소 추적 요인 분석의 점근 적 바이어스. Psychometrika65,413-425. 쨈챘짹쨀째쩔징 쨉청쨋처 쨘쨍쩔징 쨈챘쩔짤 쨘쨍쩔징 쨈챘쩔짤 쨘쨍쩔징 쨈챘쩔짤 쨘쨍쩔징 쨈챘쩔짤 쨘쨍쩔징 쨈챘쩔짤 쨘쨍쩔징 쨈챘쩔짤 쨘쨍쨈쨈. 테스트의 신뢰성과 unidimensionality 의 가설에 가장 큰 하한선. Psychometrika69,613-625. 도이:10.,쩔짤쨌짱쨘째쩍 짹쨍쨌짹쨍 쨉챨철쨌 32 짹챈 30,13 첸 쩔짙쩔징징쩔짙째챠쨉쨉()째챠째쨈쩌쩐(1688-7662 비균질 항목으로 구성된 시험에서 총 점수의 신뢰성에 대한 하한:II:가장 큰 하한을 찾는 검색 절차. 사이코 메트릭 42,579-591. doi:10.1007/BF02295980
CrossRef 전체 텍스트|Google 학술검색
부록 I
R 문 신뢰성 추정계수에서 피어슨”s 의 상관 관계 행렬이 있습니다., 상관관계를 벗어나는 값이 대각선은 곱하여 인자로드 항목:(1)tau-해당 모델들은 모두 동일하 0.3114(λiλj=0.558×0.558=0.3114)및(2)congeneric 모델들이 다 함수로서의 다른 요소이드(예:매트릭스 요소 a1,2=λ1λ2=0.3×0.4=0.12). 두 예제 모두에서 진정한 신뢰도는 0.731 입니다.
>omega(Cr,1)$alpha#standardized Cronbach”s α
0.731
>omega(Cr,1)$omega.tot#계수 ω 합계
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach”s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731