“나는,어떤 평가,확신하는 그는 주사위를 던지지 않는다.,”
~아인슈타인이
- 임의의 변수를
- 이산수
- 지속적인 임의의 변수를
- 혼합수
- 누적분포의 기능(누적분포함수)
- 확률 밀도 함수(PDF)
- 인터랙티브 CDF/PDF 예
수:

말은 당신을 당신의 주머니에서 동전 던져 있습니다. 그것이 공간을 뒤집는 동안,당신은 아마도 그 미래에 대해 무엇을 말할 수 있습니까?
착륙 할 것인가? 꼬리?, 그 이상,얼마나 오래 공중에 남아있을 것인가? 몇 번이나 튕겨 나올까요? 그것이 처음으로 땅에 닿는 곳에서 얼마나 멀리 떨어져 마침내 쉬게 될 것입니까? 그 문제에 대해,그것은 이제까지 땅에 부딪 힐 것인가? 쉬러 온 적 있니?
일부 이러한 질문,우리가 할 수 있고 해결에 답변하기 전에 긴 관측;우리는 확실한 중력을 개최하고 동전은 땅입니다. 그러나 다른 사람을 위해 우리가 선택의 여지가 없지만을 보류 판단을 말하고 더 많은 모호한 측면 경우,우리는 말하고자하는 유용한 아무것도 미래에 대한 모든.,
과학자로서,그것은 물론,유용한 무언가를 말하는 우리의 일이다(또는 아주 적어도,권위…),중요한 물리적 시스템의 은유 적 동전은 여전히 공중에 있습니다. 머리 나 꼬리는 삶이나 죽음의 문제 일 수도 있습니다. 우리의 동전은 예를 들어 가능한 다양한 냉각수 유량 또는 원자력 발전소의 우라늄 질량 일 수 있습니다. 우리는 우리의 기회는 우리가 대신 붕괴의 터빈을 잉 얻을 것이다 무엇을 알고 크게 걱정.,
엄격한 결정 론자에게,그러한 모든 베팅은 은유 적이든 아니든 동전이 발행되기 훨씬 전에 해결되었습니다. 우리가 동전 던지기,질량의 정확한 분포,방에있는 공기의 다양한 분 움직임에 적용된 힘만 알았다면… 만약 우리가 모든 것을 알고,그 후에 우리가 알고 있는 특별한 동전 던지기가 있었 100%의 기회를 방문의 방법으로는 토지,그리고 제의 기회를 다른 결과입니다.
그러나 우리는 물론 세계에 대한 그러한 지식의 언급 할 수없는 부분조차도 부족한 경우가 많습니다., 또한,그것은 것에 대단히 작은 규모는 엄격한 determinists 은 절대적으로 잘못이 없는 방법 예측하는 경우,예를 들어,원자 우라늄 분할됩니다,그리고 이러한 경우 이벤트에 영향을 미치는 더 큰 세계를 한 다음 매크로 행사가 진정으로 예측할 수 없습니다. 일부 결과는 진정으로 공중에 올라 있으며,과거의 일부가 될 때까지 불안해합니다. 이 현실에 대처하고 시스템의 미래 상태를 몇 가지 유용한 방법으로 설명 할 수 있도록하기 위해 무작위 변수를 사용합니다., 랜덤 변수는 단순히 시스템의 가능한 각 물리적 결과를 고유 한 실제 수와 관련시키는 함수입니다. 이와 같이 이산,연속 및 혼합의 세 가지 종류의 무작위 변수가 있습니다. 다음 섹션에서는 이러한 범주가 간략하게 논의되고 예제가 제공됩니다.
이산 무작위 변수:
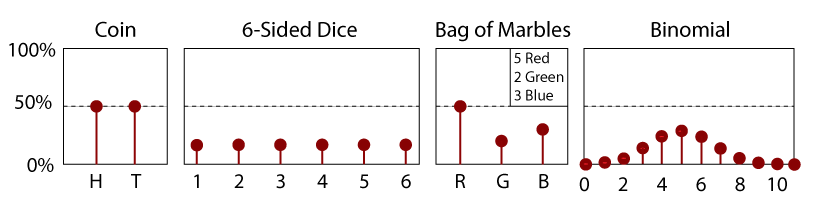
우리의 동전 던지기를 다시 생각해보십시오. 우리는 가능한 결과로 머리 또는 꼬리를 가질 수있었습니다. 우리가 변수 인 x 를 단일 토스의 머리 수로 정의했다면 x 는 아마도 1 또는 0 일 수 있습니다., 이러한 함수 인 x 는 이산 랜덤 변수의 예가 될 것입니다. 이러한 무작위 변수는 이산 값에만 걸릴 수 있습니다. 다른 예는 임신 테스트의 가능한 결과 또는 클래스 룸의 학생 수 일 것입니다.
Continuous Random Variables:
시 동전 던지,만약 우리가 우리가고 싶다고 설명하는 사이의 거리는 우리의 동전에 온 나머지고 그 수 있습니다. 는 거리,x,이 될 것이 지속적인 랜덤변수할 수 있기 때문에 가서의 무한한 값에서 지속적인 범위의 번호입니다., 동전은 1cm 또는 1.1cm 또는 1.11cm 또는 계속해서 여행 할 수 있습니다. 다른 예로는 지속적인 임의의 변수가 될 것이 별에서 우리의 갤럭시,pH 의 바다 또는 거주지 시간의 몇 가지 실정에서 가스 크로마토그래프.
혼합 랜덤 변수:
혼합 랜덤 변수는 이산 및 연속 구성 요소를 모두 가지고 있습니다. 이러한 무작위 변수는 드물게 발생합니다. 가능한를 들어,하지만,당신이 될 수 있습 샘플 측정”을 통해 빠르고 안전하게 결정하는 어떤 무게 측정된 음의 값으로 받게 될 것입니다 값은 0 입니다., 그런 식으로 랜덤 변수는 x=0 의 개별 구성 요소와 x>0 의 연속 구성 요소를 갖습니다.
누적분포의 기능(CDF):
질문은 물론,는 방법으로 발생하는 최고의 수학적으로 설명하고(시각적으로 표시)random variables. 이러한 작업에는 확률 밀도 함수(PDF)와 누적 밀도 함수(CDF)를 사용합니다. CDFs 는 Pdf 보다 이산 및 연속 랜덤 변수 모두에 대해 이해하기가 더 간단하므로 먼저 CDFs 를 설명 할 것입니다.
공정한 6 시드 주사위를 던지기를 고려하십시오., 우리는 무작위 변수의 가능한 값 중 하나를 얻을 수있는 6 분의 1 의 기회를 가질 것입니다(1, 2, 3, 4, 5, 또는 6). 면 우리는 줄거리들이 가능값 x 축과 플롯을 확률을 측정하는 각 특정 값,x,또는 어떤 값보다 적은 x y 축에,우리는 것이 누적분포함수의 임의 변수입니다. 이 경우 주사위는 주사위보다 훨씬 작아야하며 주사위보다 작아야하며 주사위는 주사위보다 작아야합니다. 각 단계의 높이는 16.67%또는 6 에서 1 입니다.
이 함수 인 CDF(x)는 x 를 포함하여 모든 값을 측정 할 확률을 간단히 알려줍니다., 따라서 모든 Cdf 는 모두 이러한 특성을 가져야합니다.
- A CDF 는 x=-∞일 때 0 과 같아야하며 x 가+∞에 접근함에 따라 1(또는 100%)에 접근해야합니다. 간단히 말해,모든 가능한 결과가 있어야 합 결과의 기회를 던지는 여섯면 주사위 점점 사이의 값을-∞및∞은 100%이다.
- CDF 의 기울기는 항상 0 과 같거나 커야합니다. 예를 들어,6 시드 주사위를 던지거나(공정하거나 그렇지 않은 경우)0 에서 4 사이의 값을 얻을 수있는 기회를 고려하십시오., 그 기회를 가능하게 될 것보다 더 많은 기회를 얻 사이의 값을 0 5 기 때문에,확률이 1,2 또는 3 상륙 얼굴은,물론,항상 어떤 부분의 가능성에 대한 1,2,3 또는 4 입니다.
연속 랜덤 변수의 예를 들어,다음 애플릿은 정상적으로 분산 된 CDF 를 보여줍니다.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., CDF 의 특성은 위에서 설명하고 연속 랜덤 변수에 대한 이산 랜덤 변수 홀드에 대해 설명했음을 간단히 알 수 있습니다.
CDFs 의 속성에 대한보다 직관적 인 예는 아래의 대화 형 예제를 참조하십시오. 또한,대화 형 플롯의 많은 다른 CDFs 중요한 분야 통계와 이 사이트에서 사용되는 여기에서 찾을 수 있습니다.
확률 밀도 함수(PDF):
PDF 에 대한 공정한 6-Sidded 니다.
PDF 는 단순히 CDF 의 파생물입니다., 따라서 PDF 는 랜덤 변수 인 x 의 함수이기도하며 그 크기는 특정 값을 측정하는 상대적 가능성에 대한 표시 일 것입니다. 이 CDF 의 기울기이기 때문에,PDF 는 항상 양수이어야한다;어떤 이벤트에 대한 부정적인 확률은 없습니다. 또한 정의에 따르면-∞와 x 사이의 PDF(x)곡선 아래 영역은 CDF(x)와 같습니다. 따라서 두 값 x1 과 x2 사이의 영역은 해당 범위 내의 값을 측정 할 확률을 제공합니다.
다음 애플릿은 일반적으로 분산 된 랜덤 변수 인 x 에 대한 PDF 의 예를 보여줍니다.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
| |
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., 또한 연속 PDF 와 이산 PDF 의 차이점을 고려하십시오. 는 동안 이산 PDF(과 같은 위의 그림과를 위해 최선을 다해 노력하고)을 제공할 확률을 얻기의 특정한 결과 확률과 지속적인 Pdf 파일은 문제의 범위,개별 점이다. 예를 들어,PDF 에서 볼 수 있듯이 주사위에 3 을 굴릴 확률은 6 명 중 1 명(16.6%)이 분명합니다. 그러나 위의 그림과 같이 일반 PDF 와 평균이 0 인 무작위 변수로 정확히 0 을 측정하는 이상한 점은 무엇입니까? 비록 그것이 PDF 가 가장 큰 값이지만,정확히 0.00000 을 측정 할 수있는 기회..,. 아마도 반 직관적으로 0 입니다. 무한 정밀도 밖으로 어떤 특정 난수를 측정의 확률은,사실,제로. 연속 PDF 할 수 있습이 무엇인지 묻는 확률은 측정 것 두 값을 얻는 확률입니다. 이 확률을 찾기 위해 우리는 단순히 우리의 무작위 변수의 CDF 를 사용합니다., 기 때문에 누적분포함수는 홀수의 측정 값이는 아무거나 또는 보다 낮은 값을 찾기 위해 가능성을 측정하는 두 값 사이에,x1 과 x2(는 x1>x2),우리는 단순히 가치의 CDF 에서 1 개 및 빼기에서 그것의 가치 CDF 에 x2. 예를 들어를 사용하여,정상적인 누적분포함수 애플릿의상에(μ=0,σ=1)는 경우에,우리는 달라고 확률이 알고의 측정 0.01 및 0.02 리 CDF(x=0.1)=53.9828%고 CDF(x=0.2)=57.9260%. 그런 다음 차이 인 CDF(0.2)-cdf(0.1)는 0.1 에서 0.2 사이의 x 를 측정하는 약 3.9%의 확률을 제공합니다., Pdf 의 속성에 대한보다 직관적이고 시각적 인 예는 아래의 대화 형 예제를 참조하십시오. 또한이 사이트에서 사용되는 많은 중요한 Pdf 의 대화 형 플롯이 여기에서 볼 수 있습니다. | |||||||||||||||||