le modèle de risques proportionnels de Cox

j’ai déjà écrit sur la façon de calculer la courbe de Kaplan–Meier pour les données de survie. En tant qu’estimateur non paramétrique, il permet de donner un aperçu rapide de la courbe de survie d’un ensemble de données. Cependant, cela ne vous permet pas de modéliser l’impact des covariables sur la survie. Dans cet article, nous nous concentrerons sur le modèle de risques proportionnels de Cox, l’un des modèles les plus utilisés pour les données de survie.

nous allons approfondir la façon de calculer les estimations., Ceci est précieux car nous verrons que les estimations ne dépendent que de l’ordre des défaillances et non de leur temps réel. Nous discuterons également brièvement de certaines questions délicates sur l’inférence causale qui sont spéciales à l’analyse de la survie.

nous pensons généralement aux données de survie en termes de courbes de survie comme celle ci-dessous.,

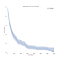
Sur l’axe des x, nous avons le temps en jours. Sur l’axe des y, nous avons (un estimateur pour) le pourcentage (techniquement, proportion) de sujets dans la population qui « survivent” à ce moment-là. Survivre peut être figuratif ou littéral., Il pourrait s’agir de savoir si les gens vivent jusqu’à un certain âge, si une machine en fait un certain temps sans tomber en panne, ou si quelqu’un reste au chômage un certain temps après avoir perdu son emploi.

surtout, la complication dans l’analyse de la survie est que certains sujets n’ont pas leur « mort” observée. Ils peuvent être encore en vie, une machine peut encore fonctionner, ou quelqu’un peut encore être au chômage au moment où les données sont collectées., De telles observations sont appelées « censurées à droite » et le traitement de la censure signifie que l’analyse de la survie nécessite différents outils statistiques.

nous désignons la fonction survivor comme S, une fonction du temps. Sa sortie est le pourcentage de sujets survivant à l’instant T. (encore une fois, il s’agit techniquement d’une proportion comprise entre 0 et 1, mais j’utiliserai les deux mots de manière interchangeable). Pour plus de simplicité, nous ferons l’hypothèse technique que si nous attendons assez longtemps, tous les sujets « mourront. »

Nous indexerons les sujets avec un indice comme i ou J., L’échec fois de l’ensemble de la population sera indiqué avec un indice similaire sur la variable de temps t.

Autre subtilité à prendre en considération est de savoir si nous sommes le traitement de temps discrets (semaine par semaine, par exemple) ou en continu. Philosophiquement parlant, nous ne mesurons le temps que par incréments discrets (à la seconde la plus proche, disons)., Généralement, nos données ne nous indiquent que si quelqu’un est décédé au cours d’une année donnée ou si une machine est tombée en panne un jour donné. Je vais aller et venir entre les cas discrets et continus dans l’intérêt de garder l’exposition aussi claire que possible.

lorsque nous essayons de modéliser les effets des covariables (par exemple, l’âge, le sexe, la race, le fabricant de la machine), nous serons généralement intéressés à comprendre l’effet de la covariable sur le taux de danger. Le taux de risque est la probabilité instantanée d’échec/décès/transition d’État à un instant T donné, conditionnée au fait d’avoir déjà survécu aussi longtemps., Nous le désignerons λ (t). Traiter le temps comme discret:

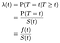
où F est la densité de probabilité globale d’échec au temps T. Nous pouvons unifier les cas discrets et continus en autorisant les fonctions Delta dans la « fonction”de densité de probabilité. Ainsi le résultat λ = f / s est le même pour le cas continu.

nous allons fixer un exemple., Considérons le contexte d’un essai clinique où un médicament provoque initialement une maladie en rémission. Nous dirons que le médicament « échoue » pour un sujet lorsque la maladie commence à progresser pour un sujet. Enfin, supposons que l’état de la maladie des sujets soit mesuré chaque semaine. Ensuite, si λ (3) = 0,1, cela signifie qu’il y a 10% de chances que, pour un sujet donné, s’il est encore en rémission avant la semaine 3, sa maladie commence à progresser à la semaine 3. Les 90% restants resteront en rémission.,

ensuite, la fonction de densité de probabilité globale f est juste la dérivée de S par rapport au temps. (Encore une fois, si le temps est discret, f est juste la somme de certaines fonctions delta).,341fa8b2″>

Cela signifie que si nous connaissons la fonction de Risque, nous pouvons résoudre cette équation différentielle S:

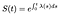
Si le temps est discret, l’intégrale d’une somme de delta fonctions transforme tout en une somme des dangers à chaque temps discret.,

D’accord, cela résume la notation et les concepts de base dont nous aurons besoin. Passons à la discussion des modèles.

modèles non, Semi Et entièrement paramétriques

Comme je l’ai dit plus tôt, nous nous intéressons généralement à la modélisation du taux de risque λ.

dans un modèle non paramétrique, nous ne faisons aucune hypothèse sur la forme fonctionnelle de λ. La courbe de Kaplan-Meier est L’estimateur du maximum de vraisemblance dans ce cas. L’inconvénient est que cela rend difficile la modélisation des effets des covariables. C’est un peu comme utiliser un nuage de points pour comprendre l’effet d’une covariable., Pas nécessairement, aussi utile qu’un modèle paramétrique comme une régression linéaire.

dans un modèle entièrement paramétrique, nous faisons une hypothèse pour la forme fonctionnelle précise de λ. Une discussion des modèles entièrement paramétriques est un article complet à part entière, mais cela vaut la peine d’une discussion très brève. Le tableau ci-dessous présente trois des modèles entièrement paramétriques les plus courants. Chacun est généralisé par le suivant, allant de 1 à 2 à 3 paramètres. La forme fonctionnelle de la fonction de danger est indiquée dans la colonne du milieu. Le logarithme de la fonction de risque est également indiqué dans la dernière colonne., Tous les paramètres (α, α, μ) sont supposés positifs sauf que μ pourrait être 0 dans la distribution de Weibull généralisée (reproduisant la distribution de Weibull).

En regardant le logarithme nous montre que le modèle exponentiel suppose que la fonction de risque est constante. Le modèle de Weibull suppose que est croissante si α>1, constante si α=1, et la diminution de si α<1., Le modèle de Weibull généralisé commence de la même manière que le modèle de Weibull (au début ln s = 0). Après cela, un terme supplémentaire μ entre en jeu.

Le problème avec ces modèles est qu’ils font des hypothèses fortes sur les données. Dans certains contextes, il peut y avoir des raisons de croire que ces modèles conviennent bien. Mais avec ces options et plusieurs autres disponibles, il existe un fort risque de tirer des conclusions incorrectes en raison d’une mauvaise spécification du modèle.

c’est pourquoi les risques proportionnels de Cox, un modèle semi-paramétrique, sont si populaires., Aucune hypothèse fonctionnelle n’est faite sur la forme de la fonction de danger; au lieu de cela, des hypothèses de forme fonctionnelle sont faites sur les effets des covariables seules.,

Le Modèle à Risques Proportionnels de Cox

Le Modèle à Risques Proportionnels de Cox est généralement donnée en fonction du temps t, le vecteur des covariables x, et le coefficient de vecteur β,

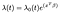
où la λₒ est une fonction arbitraire de temps, la base de danger. Le produit dotal de X et β est pris dans l’exposant tout comme dans la régression linéaire standard., Quelles que soient les covariables de valeurs, tous les sujets partagent le même risque de référence λₒ. Par la suite, des ajustements sont effectués en fonction des covariables.

interprétation des résultats

supposons pour la minute que nous avons adapté un modèle de risques proportionnels de Cox à nos données, qui consistait en

1. Une colonne spécifiant l’heure pour chaque sujet
2. Une colonne spécifiant si le sujet a été « observé” (s’il a échoué, ou, dans notre exemple préféré, si sa maladie progresse). Une valeur de 1 signifie que le sujet a eu sa progression de la maladie., Une valeur de 0 signifie que, lors de la dernière observation, la maladie n’avait pas progressé. L’observation a été censurée.
3. Colonnes pour nos covariables X.

Après l’ajustement, nous obtiendrons des valeurs pour β. Par exemple, supposons pour simplifier qu’il existe une seule covariable. Une valeur de β=0,1 signifie qu’une augmentation de la covariable d’une quantité de 1 conduit à un risque élevé d’environ 10% de progression de la maladie à un moment donné., La valeur exacte est en fait

Pour les petites valeurs de β, la valeur de β est lui-même une assez bonne approximation de l’augmentation exacte du danger. Pour des valeurs plus grandes de β, la quantité exacte doit être calculée.

Une autre façon d’exprimer β=0,1 est que, lorsque x augmente, le danger augmente à un taux de 10% par augmentation de x par 1. Le plus grand 10.,52% provient de la composition (continue), tout comme pour les intérêts composés.

de plus, β=0 signifie aucun effet, et β négatif signifie qu’il y a moins de risque à mesure que la covariable augmente. Notez que, contrairement aux régressions standard, il n’y a pas de terme d’interception. Au lieu de cela, l’interception est absorbée dans le risque de référence λₒ, qui peut également être estimé (voir ci-dessous).

enfin, en supposant que nous avons estimé la fonction de danger de base, nous pouvons construire la fonction de survivant.,

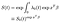
La fonction de base est élevé à la puissance de l’exp(xʹß) facteur venant des covariables. Certaines précautions doivent être prises dans l’interprétation de la fonction de survie de base, qui joue à peu près le rôle du terme d’interception dans une régression linéaire régulière. Si les covariables ont été centrées (moyenne 0), elle représente la fonction survivor pour le sujet « moyen”.,

estimation du modèle de risques proportionnels de Cox

dans les années 1970, David Cox, un mathématicien britannique, a proposé un moyen d’estimer β sans avoir à estimer le risque de référence λₒ. Encore une fois, le risque de référence peut être estimé par la suite. Comme mentionné précédemment, nous verrons que c’est l’ordre des échecs observés qui compte, pas les temps eux-mêmes.

avant de sauter dans l’estimation, il vaut la peine de discuter des liens. Comme nous n’observons généralement que les données par incréments discrets, il est possible que deux échecs se produisent en même temps., Par exemple, deux machines peuvent tomber en panne dans la même semaine et l’enregistrement n’est effectué que sur une base hebdomadaire. Ces liens rendent l’analyse de la situation assez compliquée sans ajouter beaucoup de perspicacité. Par conséquent, je calculerai les estimations en cas d’absence de liens.

rappelons que nos données consistent en des observations de certaines défaillances de nombres à un moment discret. Soit R (t) la population « à risque” à l’instant T. si un sujet de notre étude a échoué (la maladie a progressé, par exemple) avant l’instant t, ils ne sont pas « à risque »., »De plus, si un sujet de notre étude a vu son observation censurée à un moment avant l’Heure t, il n’est pas non plus « à risque. »

de la manière habituelle, nous voulons construire une fonction de vraisemblance (Quelle est la probabilité que nous aurions observée les données que nous avons faites, compte tenu des covariables et des coefficients), puis l’optimiser pour obtenir un estimateur de maximum de vraisemblance.

pour chaque instant discret où nous avons observé une défaillance du sujet j, la probabilité que cela se produise, étant donné qu’une défaillance s’est produite, est inférieure. La somme est prise en charge par tous les sujets à risque au moment J.,

Notez que la base de danger λₒ a abandonné! Très pratique. Pour cette raison, la probabilité que nous construisons n’est qu’une probabilité partielle. Notez également que les temps n’apparaissent pas du tout., Le terme pour le sujet j ne dépend que des sujets qui sont encore en vie au moment j, qui à son tour ne dépend que de l’ordre dans lequel les sujets sont censurés ou observés comme échouant.

la probabilité partielle n’est bien sûr que le produit de ces termes, un pour chaque échec que nous observons (pas de termes pour les observations censurées).,

la probabilité partielle logarithmique est alors

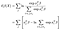
l’ajustement se fait avec des méthodes numériques standard, par exemple dans le paquet python statsmodels et la matrice variance-covariance pour les estimations est donnée par la matrice d’information Fisher (inverse de la). Rien d’excitant ici.,

estimation de la fonction de survie de base

maintenant que nous avons estimé les coefficients, nous pouvons estimer la fonction de survie. Cela finit par être très similaire à l’estimation d’une courbe de Kaplan–Meier.

nous postulons des termes α indexés par I. au moment i, la courbe de survie de base devrait diminuer d’une fraction α représentant la proportion de sujets à risque qui échouent au moment I., En d’autres termes

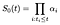
pour calculer l’estimateur du maximum de vraisemblance pour α, Nous considérons la contribution de vraisemblance du sujet i qui échoue au moment I et séparément la contribution de ceux qui sont censurés au moment I.

pour un sujet qui échoue au moment i, la probabilité est donnée par la probabilité qu’il soit vivant au moment I moins la probabilité qu’il soit vivant au moment suivant i+1. (Nous supposons Temporairement que les heures sont commandées).,

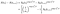
Si au lieu de cela ils sont censurés au moment i, la contribution est juste la probabilité qu’ils soient en vie au moment après I, c’est-à-dire qu’ils ne sont pas encore morts., Ceci est juste

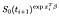
il y a un terme supplémentaire parmi les sujets qui ont été observés (c’est-à-dire observés pour échouer au lieu de censurés)., La log-vraisemblance devient

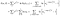
j’ai été un peu bâclée sur le fait de garder la trace des points de terminaison (je vs i+1), mais ce sera.

Il n’y a que des termes α pour les sujets que nous avons observés à échouer., En se différenciant par rapport à α-j et en supposant qu’il n’y a pas de liens, nous obtenons une contribution de la somme à gauche uniquement pour les sujets vivants à l’instant j, et une seule contribution du terme à droite.,qual à 0 signifie que nous pouvons obtenir les estimations du maximum de vraisemblance pour α En utilisant nos estimations pour β comme solution aux plusieurs équations, une pour chaque sujet qui a été observé pour échouer:

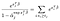
extensions et mises en garde

il y a beaucoup plus à dire sur les modèles de risques proportionnels de Cox, mais je vais essayer de garder les choses brèves et de mentionner,

par exemple, on peut envisager des régresseurs variables dans le temps, ce qui est possible.

l’autre chose cruciale à garder à l’esprit est le biais variable omis. Dans la régression linéaire standard, les variables omises non corrélées avec les régresseurs ne sont pas un gros problème. Ce n’est pas vrai dans l’analyse de survie. Supposons que nous ayons deux sous-populations de taille égale et échantillonnées dans nos données, chacune avec un taux de danger constant, l’une est de 0,1 et l’autre est de 0,5. Dans un premier temps, nous verrons un taux de risque élevé (la moyenne, seulement 0,3)., Au fil du temps, la population avec un taux de risque élevé quittera la population et nous observerons un taux de risque qui diminue vers 0,1. Si nous omettons la variable représentant ces deux populations, notre taux de risque de base sera tout foiré.