Cox Proporsjonal Farer Modell

jeg skrev tidligere om hvordan å beregne Kaplan–Meier-kurve for overlevelse data. Som en ikke-parametrisk estimator, det gjør en god jobb med å gi en rask titt på overlevelse kurve for et dataset. Men, hva det vil ikke la deg gjøre er å modellere effekten av covariates på overlevelse. I denne artikkelen vil vi fokusere på Cox Proporsjonal Farer modell, en av de mest brukte modellene for overlevelse data.

Vi vil gå inn i noen dybde på hvordan å beregne estimater., Dette er verdifulle fordi vi vil se at estimatene avhenger bare på bestilling av feil og ikke deres faktiske ganger. Vi vil også kort diskutere noen vanskelige spørsmål om kausal inferens som er spesielle for overlevelse analyse.

Vi vanligvis tenker på overlevelse data i form av overlevelse kurver som vist nedenfor.,

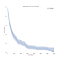
På x-aksen, har vi tid i dager. På y-aksen, vi har (en estimator for) prosentandel (teknisk del) av pasientene i befolkningen om at «overleve» til den tid. Overleve kan være figurative eller bokstavelig., Det kan være om mennesker lever til en viss alder, om en maskin som gjør det til en viss tid uten å bryte ned, eller det kan være om noen fortsatt er arbeidsledig en viss tid etter å ha mistet jobben sin.

det som er Avgjørende, den komplikasjon i survivorship analyse er at noen fag ikke har sin «død» observert. De kan fortsatt være i live, en kan maskinen fortsatt fungere, eller noen kan fortsatt være arbeidsledige i gang data samles inn., Slike observasjoner er kalt «høyre-sensurert» og arbeider med sensur betyr at overlevelsen analyse krever forskjellige statistiske verktøy.

Vi betegne den overlevende funksjon som S, en funksjon av tiden. Produksjonen er prosentandelen av fag overleve ved tid t. (Igjen, det er teknisk sett en andel mellom 0 og 1, men jeg skal bruke de to ordene om hverandre). For enkelthets skyld vil vi gjøre den tekniske forutsetningen om at hvis vi venter lenge nok alle fag vil «dø.»

Vi vil indeksere fag med en senket skrift som i eller j., Svikt ganger av hele befolkningen vil være indikert med et lignende senket på den tiden variabelen t.

En annen finesse å vurdere, er om vi er behandling av tiden som diskrete (uke etter uke, si) eller kontinuerlig. Filosofisk sett, er vi bare noensinne måle tid i diskrete intervaller (til nærmeste sekund, si)., Ofte våre data vil bare fortell oss hvis noen døde i et gitt år, eller hvis en maskin ikke klarte på en gitt dag. Jeg vil gå frem og tilbake mellom diskret og kontinuerlig tilfeller i interesser av å holde utstilling så klart som mulig.

Når vi prøver å modellere effekter av covariates (f.eks. alder, kjønn, rase, maskin produsenten) vi vil typisk være interessert i å forstå effekten av covariate på Fare Pris. Fare pris er momentant sannsynligheten for feil/død/stat overgang på et gitt tidspunkt t, betinget på allerede har overlevd så lenge., Vi vil betegne det λ(t). Behandling av tiden som diskrete:

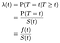
Der f er den samlede sannsynligheten tetthet av sviktende ved tid t. Vi kan forene det diskrete og kontinuerlige tilfeller ved at delta funksjoner i sannsynligheten tetthet «funksjon». Dermed resultatet λ = f/S er den samme for den kontinuerlige tilfellet.

La oss løse et eksempel., La oss vurdere rammen av en klinisk studie der et stoff som i utgangspunktet fører til en sykdom å gå inn i remisjon. Vi vil si at stoffet «mislykkes» for en gjenstand når sykdommen begynner å pågår for et emne. Til slutt, la oss anta at fag’ sykdom statuser er målt hver uke. Så hvis λ(3) = 0.1, som betyr at det er 10% sjanse for at, for et gitt motiv, hvis de fortsatt er i remisjon før uke 3, deres sykdom vil begynne å gjøre fremskritt i uke 3. De andre 90% vil være i tilbakegang.,

Neste, den generelle sannsynlighetstetthetsfunksjonen f er bare derivat av S med hensyn til tid. (Igjen, hvis tid er diskret, f er bare summen av noen delta funksjoner).,341fa8b2″>

Dette betyr at hvis vi vet Fare funksjon, kan vi løse dette differensial ligningen for S:

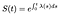
Hvis tid er diskret, integralet av en sum av delta funksjoner bare blir til en sum av farer på hver diskret tid.,

Okay, som oppsummerer notasjon og grunnleggende begreper som vi trenger. La oss gå videre til å diskutere modeller.

Ikke-, Semi-og Fullt-Parametriske Modeller

Som jeg sa tidligere, vi er vanligvis interessert i modellering Fare Pris λ.

I en ikke-parametrisk modell, gjør vi ingen forutsetninger om funksjonell form av λ. Den Kaplan–Meier-Kurven er Maximum Likelihood-Funksjonen i dette tilfellet. Ulempen er at dette gjør det vanskelig å modellere effekter av covariates. Det er litt som å bruke et scatter plott for å forstå effekten av en covariate., Ikke nødvendigvis like nyttig som en fullt parametrisk modell som en lineær regresjon.

I en fullt parametrisk modell, gjør vi en antakelse for presis funksjonell form av λ. En diskusjon av fullt parametriske modeller er en full artikkel i sin egen rett, men det er verdt et veldig kort diskusjon. Tabellen nedenfor viser tre av de mest vanlige fullt-parametriske modeller. Hver er generalisert av den neste, går fra 1 til 2 til 3 parametre. Funksjonell form for fare funksjon vises i den midterste kolonnen. Logaritmen av fare-funksjonen er også vist i siste kolonne., Alle parametere (ɣ, α, μ) er antatt å være positiv, bortsett fra at μ kan være 0 i generalisert Weibull distribution (reprodusering av Weibull distribution).

Se på logaritmen viser oss at den eksponensielle modellen tar utgangspunkt i at fare-funksjonen er konstant. Den Weibull-modellen forutsetter at det er økende hvis α>1, konstant hvis α=1, og redusere hvis α<1., Generalisert Weibull-modellen starter på samme måte som Weibull-modellen (i begynnelsen ln S = 0). Etter at en ekstra sikt μ spark.

problemet med disse modellene er at de gjør sterke forutsetninger om data. I visse sammenhenger, kan det være grunn til å tro at disse modellene er en god passform. Men med disse og flere andre alternativer som er tilgjengelig, det er en sterk risiko for å trekke feil konklusjoner på grunn av misspecification av modellen.

Dette er grunnen til at Cox Proporsjonal Farer, en semi-parametrisk modell er så populære., Ingen funksjonelle forutsetninger som er gjort om form av Fare Funksjon; i stedet, funksjonell form forutsetninger som er gjort om virkninger av covariates alene.,

Cox Proporsjonal Farer Modell

Cox Proporsjonal Farer Modellen er vanligvis gitt i form av tid t, covariate vektor x, og koeffisienten vektor β som

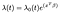
der λₒ er en vilkårlig funksjon av tid, baseline fare. Prikk-produktet av X og β er tatt i eksponenten akkurat som i vanlig lineær regresjon., Uavhengig av verdier covariates, alle fag dele samme baseline fare λₒ. Deretter justeringer er gjort basert på covariates.

Tolkning av Resultatene

Tenk for liten til at vi har plass en Cox Proporsjonal Farer modellen til våre data, som besto av

1. En kolonne angi klokkeslett for hvert fag
2. En kolonne som viser om emnet var «observert» (å ha sviktet, eller, i vårt anbefalte eksempel å ha sykdommen pågår). En verdi på 1 betyr at faget hadde sykdommen pågår., En verdi på 0 betyr at i det siste observasjon tid hadde sykdommen ikke er kommet. Observasjonen ble sensurert.
3. Kolonner for våre covariates X.

Når det passer, vil vi få verdier for β. For eksempel, la oss anta for enkelthets skyld at det er en enkelt covariate. En verdi av β=0.1 betyr at en økning i covariate av et beløp på 1 fører til en ca 10% høy sjanse for progresjon av sykdommen til enhver tid., Den nøyaktige verdien er faktisk

For små verdier av β, verdien av β i seg selv er en ganske god tilnærming til den eksakte økning i fare. For større verdier av β, det eksakte beløpet må beregnes.

en Annen måte å uttrykke β=0.1 er at, som x øker, øker faren øker med en sats på 10% per øke i x med 1. De større 10.,52% kommer fra (kontinuerlig) compounding, akkurat som med rentes rente.

Også, β=0 betyr ingen effekt, og β negativ, betyr det at det er mindre risiko som covariate øker. Vær oppmerksom på at, i motsetning til i standard-regresjoner, det er ingen fange opp sikt. I stedet skjæringspunktet er absorbert inn i baseline fare λₒ, som kan også være beregnet (se nedenfor).

til Slutt, forutsatt at vi har estimert baseline fare funksjon, kan vi konstruere den overlevende funksjon.,

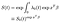
Den opprinnelige funksjonen er opphøyd i den exp(xʹß) faktor kommer fra covariates. Noen bør være forsiktig i tolkningen av baseline-survivor-funksjonen, som grovt spiller en rolle i skjæringspunktet begrepet i en vanlig lineær regresjon. Hvis covariates har vært sentrert (gjennomsnitt 0) da den representerer den overlevende funksjon for «gjennomsnitt» av emnet.,

Estimere Cox Proporsjonal Farer Modell

På 1970-tallet, David Cox, en Britisk matematiker, har foreslått en måte å anslå β uten å måtte beregne baseline fare λₒ. Igjen, baseline fare kan være estimert etterpå. Som nevnt tidligere, vil vi se at dette er er bestilling av observerte feil som teller, ikke de gangene seg selv.

Før du hopper inn i beregningen, det er verdt å diskutere bånd. Siden vi vanligvis bare ser på data i diskrete intervaller, det er mulig at to feil kan oppstå på samme tid., For eksempel, to maskiner kan mislykkes i den samme uken, og innspillingen er gjort på en ukentlig basis. Disse båndene gjør analyse av situasjonen ganske komplisert uten å legge til mye innsikt. Derfor vil jeg utlede anslagene i tilfelle av ingen bånd.

Husker at våre data består av observasjoner av et antall feil i diskret tid. La R(t) betegne befolkningen «i fare» ved tid t. Hvis et motiv i vår studie har mislyktes (sykdommen utviklet seg, for eksempel) før tiden t, de er ikke «i fare.,»Også, hvis et motiv i vår studie har hatt sin observasjon sensurert på en gang før tiden t, de er heller ikke «i fare.»

På vanlig måte, vi ønsker å konstruere en likelihood-funksjon (hva er sannsynligheten for at vi ville ha observert de data vi gjorde, gitt covariates og koeffisienter), og deretter optimalisere at for å få en maximum-likelihood-funksjonen.

For hver diskret tid når vi observert en svikt i emnet j, sannsynligheten for at det skjer, gitt at en feil oppstod, er nedenfor. Summen tas over alle fag på risiko i gang j.,

legg Merke til at den opprinnelige fare λₒ har droppet ut! Veldig praktisk. Av denne grunn, er det sannsynlig vi konstruere bare er en liten sannsynlighet. Legg også merke til at tiden ikke vises i det hele tatt., Begrepet gjenstand for j avhenger bare på hvilke temaer som fortsatt er i live på tidspunktet j, som i sin tur bare avhenger av i hvilken rekkefølge emnene er sensurert eller observert til å mislykkes.

Den delvise sannsynligheten er selvfølgelig bare produktet av disse vilkårene, ett for hver feil vi observerer (ingen vilkår for sensurerte observasjoner).,

logg delvis sannsynligheten er da

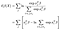
fit er gjort med standard numeriske metoder, for eksempel i python pakken statsmodels og varians-covariance matrise for beregningene er gitt ved (inverse av) Fisher-Informasjon Matrise. Ikke noe spennende her.,

Estimere Baseline Overlevende Funksjon

Nå som vi har estimert koeffisientene, kan vi anslå den overlevende funksjon. Dette ender opp med å bli svært lik for å beregne en Kaplan–Meier-kurven.

Vi postulere vilkår α indeksert av jeg. På tiden jeg, baseline overlevende kurve bør reduseres ved en brøkdel α representerer den andel av pasientene i fare som ikke på tid som jeg., Med andre ord

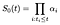
for Å beregne maximum likelihood-funksjonen for α, vi anser sannsynligheten bidrag fra fag jeg som mislykkes i gang jeg og separat bidraget fra de som er sensurert på tiden jeg.

For en gjenstand som mislykkes i tid jeg sannsynligheten er gitt ved sannsynligheten for at de er i live på tidspunktet jeg mindre sannsynlighet for at de er i live på det neste gang jeg+1. (Vi midlertidig overta ganger er bestilt).,

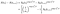
Hvis du i stedet de er sensurert på tiden jeg, bidrag er bare sannsynligheten for at de er i live på det tidspunktet da jeg, det vil si at de har ikke dødd ennå., Dette er bare

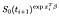
Det er en ekstra begrepet fra de fagene som ble observert (dvs. observert til å mislykkes i stedet for å sensurert)., Log likelihood blir

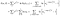
jeg har vært litt slurvete om å holde styr på endepunkter (jeg vs. i+1), men det vil alt arbeid ut.

Det er bare α vilkår for motiver som vi observerte for å mislykkes., Differensiering med hensyn til α-j og forutsatt ingen bånd, får vi et bidrag fra summen på venstre side bare for motiver som er i live på tidspunktet j, og et enkelt bidrag fra uttrykket på høyre side.,qual til 0, betyr at vi kan oppnå maksimum likelihood estimatene for α ved hjelp av våre estimater for β som løsning til flere ligninger, en for hvert fag som ble observert til å mislykkes:

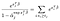
Utvidelser og Begrensninger

Det er mye mer å si om Cox Proporsjonal Farer modeller, men jeg vil prøve å holde det kort og bare for å nevne et par ting.,

For eksempel, kan man vurdere å tidsvarierende regressors, og dette er mulig.

Den andre viktige tingen å huske på er utelatt variabel skjevhet. I standard lineær regresjon, utelatte variable ukorrelerte med regressors er ikke et stort problem. Dette er ikke sant i overlevelse analyse. Anta at vi har to like store og samplet sub-populasjoner i våre data hver med en konstant fare pris, er 0,1 og den andre er 0.5. I første omgang vil vi se en høy fare pris (gjennomsnittlig, bare 0.3)., Som tiden går, befolkningen med en høy fare pris vil la befolkningen, og vi vil observere en fare pris som avtar mot 0.1. Hvis vi utelatt variabel som representerer disse to populasjoner, vår baseline fare pris vil være alt messed up.