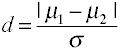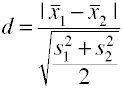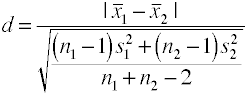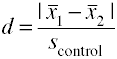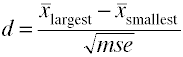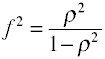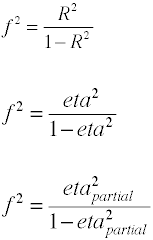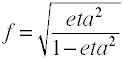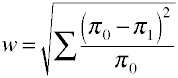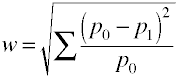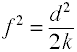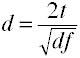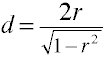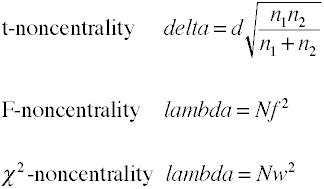En bruk av effekt-størrelse er som en standardisert indeks som er uavhengig av utvalgsstørrelse og kvantifiserer omfanget av forskjellen mellom populasjoner eller forholdet mellom forklarende og svar variabler. En annen bruk av effektstørrelse er dets bruk i performingpower analyse.
effektstørrelse for forskjellen i betyr
effektstørrelse for forskjeller i metoder er gitt byCohen s d er definert i form av befolkningen betyr (µs) og en befolkning standarddeviation (σ), som vist nedenfor.,
Det er flere forskjellige måter at man kunne estimere σ fra eksempeldata whichleads til flere varianter innenfor Cohen ‘ s d-familien.
Bruke root mean square standardavvik
ved Hjelp av samlet standardavvik (Hedges’ g)
Denne versjonen av Cohen ‘s d bruker samlet standardavvik og er også kjent som Hekker’ g.,
Du kan enkelt få denne verdien fra en anova-programmet ved å ta kvadratroten av den meansquare feil som er også kjent som root mean square error.
ved Hjelp av kontrollgruppen standardavvik (Glass’ Δ)
en Annen versjon av Cohen ‘s d ved hjelp av standardavviket for kontrollgruppen er også kjent asGlass’ Δ.,
Mer enn to grupper
Når det er mer enn to grupper bruke forskjellen mellom den største og smallestmeans dividert med kvadratroten av den mean square error.
effektstørrelse for F-prosenter i regresjonsanalyser
For OLS-regresjon mål på effekter størrelse er F som er definert av Cohen som følger.,
igjen, det er flere måter effekten størrelse kan beregnes fra eksempeldata. Notethat η2 er et annet navn for R2.
effektstørrelse for F-prosenter i analyse av varians
effekten størrelse som brukes i analyse av avvik er definert av forholdet til befolkningen standarddeviations.,
Selv om Cohen ‘ s f er definert som ovenfor, det er vanligvis computedby å ta kvadratroten av f2.
effektstørrelse for χ2 fra beredskaps-tabeller
en Gang vi begynner med definitional formel i form av befolkningen verdier.Effekt størrelse w er kvadratroten av den standardiserte chi-kvadrat statistikk.,
Og her er hvordan b, beregnes på grunnlag av utvalgte data.
Her er en tabell over foreslåtte verdier for lave, middels og høye effekter (Cohen, 1988). Disse verdiene bør notbe tatt som absolutter, og bør tolkes innenfor rammen av forskningsprogrammet. Verdiene forlarge virkninger er ofte overskredet i praksis med verdier Cohen ‘ s d er større enn 1.0 ikke uvanlig.,Imidlertid, ved hjelp av svært stor effekt størrelser i potensielle makt analyse er sannsynligvis ikke en god idé asit kan føre til under drevet studier.,formler
hvor k = antall grupper
Konverter t til d for to uavhengige grupper
Konverter r å d for to uavhengige grupper
Noncentrality estimater
Strøm-analyse ved hjelp av analytiske metoder krever et estimat av noncentrality som er basicallythe effekt størrelse multiplisert med en utvalgsstørrelse faktor., Her er noen formler for å estimere noncentrality.
Eksempel power analysis
Her er et eksempel som bringer sammen effekt størrelse og noncentrality i kraft analyse.
Vurdere en en-veis analyse av varians med tre grupper (k = 3). Hvis vi forventer andeta2 å like .,12 i dette tilfellet er effekten størrelse vil være
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
Med en anslått eksempel størrelse på 60 estimatet av noncentrality er
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
frihetsgrader i teller er k-1 = 3-1 = 2 mens denominator df er N-k = 60-3 = 57.Den kritiske verdien av F med 2 og 57 grader av frihet er 3.16. Noe som resulterer i en strøm av
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
derfor, en N 60 og effekt, størrelse på .369 gir en anslått effekt på ca .7.
Vi kan forbedre på kraft .7 ved hjelp av en anslått eksempel størrelse på 75 i stedet for 60., Med samme effekt, størrelse på.369, vi får en ny noncentrality estimat av
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
frihetsgrader i teller forbli den samme, mens denominator df nå lik N-k = 75-3 = 72.Den kritiske verdien av F med 2 og 72 grader av frihet til 3.12. Denne gangen strømmen
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
som er innenfor akseptable forskning grenser.
Vær oppmerksom på at ulike statistiske pakker bruker forskjellige navn og en annen rekkefølge av argumenter i en funksjon som vi har samtale noncentralFtail. Du vil få behov for å lese dokumentasjonen thatcomes med programvaren.,
Becker, L. Psykologi 590 kursmateriell. Sett 19 Jun 2009 <http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen, J. 1988. Statistisk power analysis for the behavioral sciences. Hillsdale, New Jersey:Lawrence Erlbaum Associates