α-koeffisienten er den mest brukte prosedyren for å beregne pålitelighet i anvendt forskning. Som det fremgår av Sijtsma (2009), dens popularitet er slik at Cronbach (1951) har blitt sitert som en referanse oftere enn artikkelen på oppdagelsen av DNA-dobbel helix., Likevel sine begrensninger og er godt kjent (Herre og Novick, 1968; Cortina, 1993; Yang og Grønt, 2011), noen av de viktigste å være forutsetninger for ukorrelerte feil, tau-ekvivalens og normalitet.
Den forutsetning av ukorrelerte feil (feil-score av alle par av elementer er ukorrelerte) er en hypotese av Klassisk Test Teori (Herre og Novick, 1968), brudd på som kan indikere tilstedeværelse av complex flerdimensjonal strukturer som krever estimering prosedyrer som tar denne kompleksiteten i betraktning (f.eks., Tarkkonen og Vehkalahti, 2005; Grønn og Yang, 2015)., Det er viktig å utslette den feilaktige troen på at α-koeffisienten er en god indikator på unidimensionality fordi dens verdi ville bli høyere hvis skala ble unidimensional. Faktisk det motsatte er tilfelle, som ble vist av Sijtsma (2009), og dens anvendelse i slike forhold kan føre til pålitelighet blir sterkt overvurdert (Raykov, 2001). Derfor, før du beregner α det er nødvendig å kontrollere at data passer unidimensional modeller.
forutsetningen for tau-ekvivalens (dvs., det samme er sant score for alle test-produkter, eller tilsvarende faktor belastninger av alle elementer i en fakultet-modellen) er et krav for α å være tilsvarende den reliability koeffisient (Cronbach, 1951). Hvis forutsetningen for tau-ekvivalens er brutt den sanne reliability verdien vil være undervurdert (Raykov, 1997; Graham, 2006) med et beløp som varierer mellom 0,6 og 11,1% avhengig av alvoret i overtredelsen (Grønn og Yang, 2009a). Arbeide med data som er i samsvar med denne forutsetningen er vanligvis ikke gjennomførbart i praksis (Teo og Vifte, 2013); den congeneric modell (dvs., ulike faktor belastninger) er mer realistisk.
behovet for multivariant normalitet er mindre kjent, og påvirker både puntual reliability estimering og muligheten for å etablere konfidensintervaller (Dunn et al., 2014). Sheng og Sheng (2012) observert nylig at når fordelingen er skjev og/eller leptokurtic, en negativ skjevhet er produsert når koeffisienten α er beregnet; tilsvarende resultater ble presentert av Grønt og Yang (2009b) i en analyse av effektene av ikke-normale fordelinger i vurderingen av pålitelighet., Studie av utvalgsfeil problemer er mer viktig når vi ser at det i praksis forskere fast arbeid med skjeve stolper (Micceri, 1989; Norton et al., 2013; Ho og Yu, 2014). For eksempel, Micceri (1989) har anslått at om lag 2/3 av muligheten, og over 4/5 av psykometriske tiltak utstilt minst moderat asymmetri (dvs., frafallsskjevhet rundt 1). Til tross for dette, virkningen av utvalgsfeil på pålitelighet estimering har vært lite studert.,
Vurderer den rike litteraturen på begrensninger og fordommer av α-koeffisienten (Revelle og Zinbarg, 2009; Sijtsma, 2009, 2012; Cho og Kim, 2015; Sijtsma og van der Kista stod, 2015), oppstår spørsmålet hvorfor forskere fortsette å bruke α når alternative koeffisienter som finnes omgå disse begrensningene. Det er mulig at det overskytende av prosedyrer for å beregne pålitelighet utviklet i forrige århundre har oscured debatten. Dette ville ha blitt ytterligere forsterket av enkelhet av beregne denne koeffisienten og sin tilgjengelighet i kommersiell programvare.,
vanskeligheten av å estimere pxx’ reliability koeffisienten ligger i dets definisjon pxx’=σt2∕σx2, som inneholder det sanne resultat i strid teller når dette er av natur ikke-observerbar. De α-koeffisienten prøver å omtrentlig dette uobserverbare avvik fra covariance mellom elementene eller komponenter. Cronbach (1951), viste at i fravær av tau-ekvivalens, og α-koeffisienten (eller Guttman»s lambda-3, noe som tilsvarer α) var en god nedre grense tilnærming., Dermed, når forutsetningene er brutt problemet oversettes til å finne den best mulige nedre grense; faktisk har dette navnet er gitt til den Største Nedre grensen metode (GLB) som er best mulig tilnærming fra en teoretisk vinkel (Jackson og Agunwamba, 1977; Woodhouse og Jackson, 1977; Shapiro og ti Berge, 2000; Sočan, 2000; ti Berge og Sočan, 2004; Sijtsma, 2009). Imidlertid, Revelle og Zinbarg (2009) mener at ω gir en bedre nedre grense enn GLB., Det er derfor en uløst debatt om hvilken av disse to metodene gir det beste nedre grense; videre spørsmål av ikke-normalitet har ikke blitt grundig undersøkt, som det foreliggende arbeidet omhandler.
ω Koeffisienter
McDonald (1999) foreslo wt-koeffisienten for å beregne pålitelighet fra et fakultet analyse rammeverk, som kan uttrykkes formelt som:
Hvor λj er lasting av element j, λj2 er communality av element j og ψ tilsvarer det unike., Wt-koeffisienten, ved å inkludere lambdaer i sine formler, er egnet både når tau-ekvivalens (dvs., lik faktor belastninger av alle test elementer) finnes (wt sammenfaller med matematisk α), og når elementer med forskjellige discriminations er til stede i representasjon av bygg (dvs., annen faktor belastninger av elementene: congeneric målinger). Følgelig wt korrigerer undervurdering skjevhet av α når forutsetningen for tau-ekvivalens er krenket (Dunn et al., 2014) og ulike studier viser at det er en av de beste alternativene for å beregne pålitelighet (Zinbarg et al.,, 2005, 2006; Revelle og Zinbarg, 2009), selv om det til dags dato dens funksjon i forhold til frafallsskjevhet er ukjent.
Når korrelasjon finnes mellom feil, eller det er mer enn en latent dimensjon i data, bidrag fra hver dimensjon til den totale variansen forklart er anslått å skaffe såkalt hierarkisk ω (wh) som gjør oss i stand til å korrigere den verste overestimation skjevhet av α med flerdimensjonale data (se Tarkkonen og Vehkalahti, 2005; Zinbarg et al., 2005; Revelle og Zinbarg, 2009)., Koeffisientene wh og wt er tilsvarende i unidimensional data, så vil vi referere til denne koeffisienten bare som ω.
Største Nedre grensen (GLB)
Sijtsma (2009) viser i en serie av studier som en av de mektigste estimatorer av pålitelighet er GLB—utledes av Woodhouse og Jackson (1977) fra de forutsetninger som er av Klassisk Test Teori (Cx = Ct + Ce)—en inter-item covariance matrise for observert element score Cx. Det brytes ned i to deler: summen av inter-item covariance matrise for elementet sant score Ct, og inter-item feil covariance matrix Ce (ti Berge og Sočan, 2004)., Dens uttrykk er:
hvor σx2 er testen varians og tr(Ce) refererer til spor av inter-item feil covariance matrise som det har vist seg så vanskelig å anslå. En løsning har vært å bruke fakultet prosedyrer slik som Minimum Rang faktoranalyse (en prosedyre som kalles glb.vå). Mer nylig GLB algebraiske (GLBa) prosedyren har blitt utviklet fra en algoritme utviklet av Andreas Moltner (Moltner og Revelle, 2015)., I henhold til Revelle (2015a) denne prosedyren tar form som er mest tro mot den opprinnelige definisjonen av Jackson og Agunwamba (1977), og det har den ekstra fordelen av å innføre en vektor å vekt elementer av betydning (Al-Homidan, 2008).
til Tross for sin teoretiske styrker, GLB har vært svært lite brukt, selv om noen nyere empiriske studier har vist at denne koeffisienten gir bedre resultater enn α (Lila et al., 2014) og α og ω (Wilcox et al., 2014)., Likevel, i små prøver, under forutsetning av normalitet, det har en tendens til å overvurdere den sanne reliability verdi (Shapiro og ti Berge, 2000), men dens funksjon under ikke-normale forhold er fortsatt ukjent, spesielt når fordelingen av elementene er asymmetrisk.
Vurderer koeffisientene er definert ovenfor, og fordommer og begrensninger for hvert objekt av dette arbeidet er å vurdere robustheten av disse koeffisientene i nærvær av asymmetrisk elementer, vurderer også forutsetningen for tau-ekvivalens og utvalgsstørrelsen.,
Metoder
Data Generasjon
data som ble generert ved hjelp av R (R Development Core Team, 2013) og RStudio (Racine, 2012) programvare, følgende fakultet modell:
hvor Xij er simulert respons av fag jeg i punkt j, λjk er lasting av element j i Faktor k (som ble generert av unifactorial-modellen); Fk er latent faktor som er generert av en standardisert normal fordeling (gjennomsnitt 0 og varians 1), og ej er det tilfeldige feil måling av hvert element også etter en standardisert normal fordeling.,
Skjeve elementer: Standard normal Xij ble forvandlet til å generere ikke-normale fordelinger ved hjelp av prosedyren som er foreslått av Headrick (2002) søker femte for polynom forvandler:
Simulert Betingelser
for Å vurdere ytelse av påliteligheten koeffisienter (α, ω, GLB og GLBa) vi jobbet med tre utvalgene (250, 500, 1000), to test størrelser: kort (6 stk) og lang (12 elementer), er to betingelser for bruk av tau-ekvivalens (ett med tau-ekvivalens og en uten, dvs.,, congeneric) og den progressive inkorporering av asymmetrisk elementer (fra alle de elementer som er normal for alle elementer som asymmetrisk). I den korte teste pålitelighet ble satt på 0.731, som i nærvær av tau-ekvivalens er oppnådd med seks elementer med faktor belastninger = 0.558, mens den congeneric modellen er hentet ved å sette faktor belastninger på verdier av 0.3, 0.4, 0.5, 0.6, 0.7, og 0.8 (se Vedlegg i). I det lange test av 12 elementer pålitelighet ble satt til 0.,845 å ta de samme verdiene som i korte teste for både tau-ekvivalens og congeneric modell (i dette tilfellet var det to elementer for hver verdi av lambda). På denne måten 120 forhold ble simulert med 1000 kopier i hvert enkelt tilfelle.
Data Analyse
De viktigste analysene ble utført ved hjelp av Psych (Revelle, 2015b) og GPArotation (Bernaards og Jennrich, 2015) pakker, som lar α og ω til å være beregnet. To datastyrte tilnærminger ble brukt for å estimere GLB: glb.fa (Revelle, 2015a) og glb.,algebraisk (Moltner og Revelle, 2015), sistnevnte jobbet med forfattere som Jakt og Bentler (2015).
for å evaluere nøyaktigheten av de ulike estimatorer i å utvinne pålitelighet, vi beregnet kvadrats av Error (RMSE) og fordommer. Den første er gjennomsnittet av differansene mellom beregnet og simulert pålitelighet og er formalisert som:
hvor ρ^ er estimert pålitelighet for hver koeffisient, ρ den simulerte pålitelighet og Nr antall kopier., De % bias kan forstås som forskjellen mellom gjennomsnittet av den estimerte pålitelighet og den simulerte pålitelighet og er definert som:
I begge indekser, jo større denne verdien er, jo større unøyaktighet av estimator, men i motsetning til RMSE, bias kan være positive eller negative, i dette tilfellet ytterligere informasjon vil bli innhentet som om koeffisienten er underslår eller overestimering av simulert reliability parameter., Følgende anbefaling av Hoogland og Boomsma (1998) verdier av RMSE < 0,05 og % bias < 5% ble vurdert som akseptabel.
Resultater
De viktigste resultatene kan sees i Tabell 1 (6 stk) og Tabell 2 (12 artikler). Disse viser RMSE og % skjevhet av koeffisientene i tau-ekvivalens og congeneric forhold, og hvordan frafallsskjevhet av testen distribusjon øker i takt med den gradvise innlemmelsen av asymmetrisk elementer.
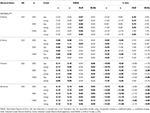
Tabell 1., RMSE og Bias med tau-ekvivalens og congeneric forutsetning for 6 elementer, for eksempel tre størrelser og antall av skjeve elementer.
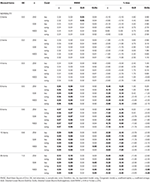
Tabell 2. RMSE og Bias med tau-ekvivalens og congeneric forutsetning for 12 elementer, for eksempel tre størrelser og antall av skjeve elementer.
Bare under forhold med tau-ekvivalens og normalitet (utvalgsfeil < 0.2) er det observert at α koeffisient estimater simulert reliability riktig, som ω., I congeneric tilstand ω korrigerer en undervurdering av α. Både GLB og GLBa presentere en positiv bias under normalitet, men GLBa viser approximatively ½ mindre % bias enn GLB (se Tabell 1). Hvis vi anser for eksempel størrelse, ser vi at mens testen størrelse øker, positiv skjevhet av GLB og GLBa avtar, men aldri forsvinner.
I en asymmetrisk forhold, som vi ser i Tabell 1 at både α og ω presentere en uakseptabel ytelse med økende RMSE og underestimations som kan nå bias > 13% for α-koeffisienten (mellom 1 og 2% lavere for ω)., Den GLB og GLBa koeffisienter presentere en lavere RMSE når testen utvalgsfeil eller antall asymmetrisk elementer øker (se Tabellene 1, 2). Den GLB koeffisient presenterer bedre estimater når testen frafallsskjevhet verdien av testen er rundt 0.30; GLBa er svært lik, som gir bedre estimater enn ω med en test frafallsskjevhet verdi rundt 0.20 eller 0.30. Imidlertid, når frafallsskjevhet verdien øker til 0,50 eller 0.60, GLB presenterer bedre ytelse enn GLBa. Test størrelse (6 eller 12 ítems) har en mye mer viktig effekt enn sample størrelse på nøyaktigheten i estimatene.,
Diskusjon
I denne studien fire faktorene var manipulert: tau-ekvivalens eller congeneric modell, sample size (250, 500 og 1000), antall test elementer (6 og 12) og antall asymmetrisk elementer (fra 0 asymmetrisk elementer til alle elementer som asymmetrisk) for å vurdere robustheten til tilstedeværelsen av asymmetrisk data i fire reliability koeffisienter analysert. Disse resultatene er diskutert nedenfor.,
I forhold til tau-ekvivalens, og α og ω koeffisienter konvergere, men i fravær av tau-ekvivalens (congeneric), ω presenterer alltid bedre estimater og mindre RMSE og % bias enn α. I denne mer realistisk tilstand derfor (Grønn og Yang, 2009a; Yang og Grønt, 2011), α blir et negativt forutinntatt reliability estimator (Graham, 2006; Sijtsma, 2009; Cho og Kim, 2015) og ω er alltid å foretrekke fremfor α (Dunn et al., 2014). I tilfelle av ikke-brudd på forutsetningen om normalitet, ω er den beste estimator av alle koeffisientene evaluert (Revelle og Zinbarg, 2009).,
Slå til prøven størrelse, ser vi at denne faktoren har en liten effekt under normale eller en liten avgang fra normalitet: den RMSE og fordommer avta som utvalgsstørrelsen øker. Likevel kan det sies at for disse to koeffisientene, med eksempel størrelse på 250 og normalitet vi får relativt nøyaktige estimater (Tang og Cui, 2012; Javali et al., 2011)., For GLB og GLBa koeffisienter, som utvalgsstørrelsen øker RMSE og fordommer har en tendens til å avta, men de opprettholder en positiv skjevhet for den tilstand av normalitet selv med stort utvalg størrelser av 1000 (Shapiro og ti Berge, 2000; ti Berge og Sočan, 2004; Sijtsma, 2009).
For test størrelse, er vi generelt observere en høyere RMSE og bias med 6 elementer enn med 12, noe som tyder på at høyere antall elementer, jo lavere RMSE og fordommer av estimatorer (Cortina, 1993). Generelt er trenden opprettholdes for både 6 og 12 elementer.,
Når vi ser på effekten av gradvis innlemme asymmetrisk elementer i datasettet, ser vi at α-koeffisienten er svært sensitive for asymmetrisk elementer, og disse resultatene er lik de som finnes av Sheng og Sheng (2012) og Grønn og Yang (2009b). Koeffisient ω presenterer lignende RMSE og bias verdiene til de av α, men litt bedre, selv med tau-ekvivalens. GLB og GLBa er funnet å presentere bedre estimater når testen frafallsskjevhet avviker fra verdier nær 0.
tatt i Betraktning at i praksis er det vanlig å finne asymmetriske data (Micceri, 1989; Norton et al.,, 2013; Ho og Yu, 2014), Sijtsma»s forslag (2009) ved hjelp av GLB som en reliability estimator synes velbegrunnet. Andre forfattere, som for eksempel Revelle og Zinbarg (2009) og Grønn og Yang (2009a), anbefaler bruk av ω, men denne koeffisienten bare har gitt gode resultater i den tilstand av normalitet, eller med lave andelen av utvalgsfeil elementer. I alle fall, disse koeffisientene er presentert større teoretisk og empirisk fordeler enn α. Likevel, vi anbefaler forskere å studere ikke bare punktlig estimater, men også til å gjøre bruk av intervall-estimering (Dunn et al., 2014).,
Disse resultatene er begrenset til den simulerte forhold, og det er antatt at det er ingen sammenheng mellom feil. Dette ville gjøre det nødvendig å gjennomføre ytterligere undersøkelser for å evaluere hvordan de ulike reliability koeffisienter med mer komplekse flerdimensjonale strukturer (Reise, 2012; Grønt og Yang, 2015) og i nærvær av ordenstallet og/eller kategoriske data hvor ikke-samsvar med forutsetningen om normalitet er normen.
Konklusjon
Når den samlede testresultater er normalfordelt (dvs., alle elementer er normalfordelt) ω bør være første valg, etterfulgt av α, siden de unngå overestimation problemer presentert av GLB. Imidlertid, når det er en lav eller moderat test frafallsskjevhet GLBa bør brukes. GLB er anbefalt når andelen av asymmetrisk elementer er høy, siden under disse betingelser for bruken av både α og ω som pålitelighet estimatorer er ikke tilrådelig, uansett eksempel størrelse.
Forfatter Bidrag
Utvikling av ideen om forskning og teoretiske rammeverk (DET, JA). Byggingen av det metodiske rammeverket (DET, JA)., Utvikling av R språket syntaks (DET, JA). Data-analyse og tolkning av data (DET, JA). Diskusjon av resultatene i lys av dagens teoretisk bakgrunn (JA, DET). Forberedelse og skriving av artikkel (JA, DET). Generelt, begge forfatterne har bidratt like mye til utviklingen av dette arbeidet.,
Midler
Den første forfatteren offentliggjort mottak av følgende finansiell støtte til forskning, forfatterskap, og/eller publisering av denne artikkelen: DET har mottatt økonomisk støtte fra den Chilenske Nasjonale Kommisjonen for Vitenskapelig og Teknologisk Forskning (CONICYT) «Becas Chile» Doktor Fellowship program (Grant nei: 72140548).
interessekonflikt Uttalelse
forfatterne erklærer at forskningen ble utført i fravær av kommersielle eller finansielle forhold som kan oppfattes som en potensiell interessekonflikt.
Cronbach, L. (1951)., Koeffisient alpha og den interne strukturen av tester. Psychometrika 16, 297-334. doi: 10.1007/BF02310555
CrossRef Full Tekst | Google Scholar
McDonald, R. (1999). Test Teori: en Enhetlig Behandling. Mahwah, NJ: Lawrence Erlbaum Associates.
Google Scholar
R Development Core Team (2013). R: Et Språk og Miljø for Statistical Computing. Wien: R Grunnlag for Statistiske beregningsmetoder.
Raykov, T. (1997)., Scale reliability, cronbach»s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package «psych.,»Tilgjengelig online på: http://org/r/psych-manual.pdf
Shapiro, A., og ti Berge, J. M. F. (2000). Den asymptotiske skjevhet av minimum spore faktor analyse, med søknader til den største nedre grensen for å pålitelighet. Psychometrika 65, 413-425. doi: 10.1007/BF02296154
CrossRef Full Tekst | Google Scholar
ti Berge, J. M. F., og Sočan, G. (2004). Den største nedre grensen for å påliteligheten til en test av hypotesen unidimensionality. Psychometrika 69, 613-625. doi: 10.,1007/BF02289858
CrossRef Full Tekst | Google Scholar
Woodhouse, B., og Jackson, P. H. (1977). Nedre grense for påliteligheten av total score på en test som består av ikke-homogene produkter: II: et søk fremgangsmåte for å finne den største nedre grensen. Psychometrika 42, 579-591. doi: 10.1007/BF02295980
CrossRef Full Tekst | Google Scholar
Vedlegg I
R-syntaks for å beregne pålitelighet koeffisienter fra Pearson ‘ s korrelasjon matriser., Korrelasjonen verdier utenfor diagonalen er beregnet ved å multiplisere faktor lasting av elementer: (1) tau-tilsvarende modell de er alle lik 0.3114 (λiλj = 0.558 × 0.558 = 0.3114) og (2) congeneric modell de varierer som en funksjon av ulike faktor lasting (f.eks., matriseelementet a1, 2 = λ1λ2 = 0.3 x 0.4 = 0.12). I begge eksempler er den sanne reliability er 0.731.
> omega(Cr,1)$alpha # standardisert Cronbach ‘ s α
0.731
> omega(Cr,1)$omega.tot # koeffisient ω sum
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach»s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731