Tilfeldige Variabler Prosjekter Lab, University of Utah

Posted on

«jeg, i alle fall, er overbevist om at Han ikke kaste terningene.,»

~ Albert Einstein

  • Tilfeldige Variabler
    • Diskrete Tilfeldige Variabler
    • Kontinuerlige Tilfeldige Variabler
    • Blandet Tilfeldige Variabler
  • Kumulativ Fordeling Funksjoner (CDF)
  • sannsynlighetstetthetsfunksjonen (PDF)
  • Interaktiv CDF/PDF Eksempel

Tilfeldige Variabler:

Si at du var til å ta en mynt fra lommen og kaste den opp i luften. Mens det knipser gjennom rommet, hva kan du si om sin fremtid?

Vil det land heads-up? Mynt?, Mer enn det, hvor lang tid vil det forbli i luften? Hvor mange ganger vil det sprette? Hvor langt fra der den første treffer bakken, vil det til slutt kommer til å hvile? For den saks skyld, vil det noensinne treffer bakken? Noen gang kommer til å hvile?

For noen slike spørsmål, vi kan og vil bosette seg på svarene lenge før observasjoner; vi er ganske sikker på at alvoret holder på og mynt vil lande. Men for andre har vi ikke noe valg, men å holde dom og snakke i mer vage begreper, dersom vi ønsker å si noe fornuftig om fremtiden i det hele tatt.,

Som forskere, det er, selvfølgelig, vår jobb å si noe nyttig (eller i det minste, autoritativt…), mens den metaforiske mynter av viktige fysiske systemet er fortsatt i luften. Krone eller mynt, kan det også være et spørsmål om liv eller død. Våre mynter kan for eksempel være ulike mulige kjølevæskestrømmen priser eller masser av uran i et kjernekraftverk. Vi bryr oss sterkt til å vite hva våre sjansene er at vi vil få whirring turbiner i stedet for en nedsmelting.,

Til en streng determinist, alle slike spill var avgjort lenge før noen mynt, metaforisk eller ikke, var stadig preget; vi rett og slett ikke ennå vet det. Hvis vi bare visste krefter brukes på en mynt»s kaste, sin eksakte fordeling av massen, de ulike minutters bevegelser av luften i rommet… Hvis vi visste alle at, så vil vi vet at spesielt myntkast hadde en 100% sjanse for landing på den måten det vil lande, og null sjanse til noe annet resultat.

Men vi, selvfølgelig, er ofte mangler enda en mentionable brøkdel av slik kunnskap om verden., Videre, det ser ut på meget små skalaer som strenge determinists er helt feil, det er ingen måte å forutsi når, for eksempel, et uran atom vil dele, og hvis en slik hendelse påvirker den større verden så at makro-event er virkelig uforutsigbar. Noen utfall virkelig er oppe i luften, urolig inntil de er en del av fortiden.

for å takle denne virkelighet, og for å være i stand til å beskrive den fremtidige tilstander av et system i noen nyttig måte, vi bruker tilfeldige variabler., En tilfeldig variabel er rett og slett en funksjon som er relatert hver mulige fysiske resultatet av et system til noen unike, ekte nummer. Det er tre typer av tilfeldige variabler: diskret, kontinuerlig og blandet. I de følgende avsnittene disse kategoriene vil bli kort diskutert og eksempler vil bli gitt.

Diskrete Tilfeldige Variabler:

Vurdere vår myntkast igjen. Vi kunne ha hoder eller haler som mulig resultater. Hvis vi definert en variabel, x, som antall hoder i et enkelt kast, så x kunne muligens være 1 eller 0, ingenting annet., En slik funksjon, x, ville være et eksempel på en diskret tilfeldig variabel. Slike tilfeldige variabler kan bare ta på diskrete verdier. Andre eksempler vil være mulig resultat på en graviditetstest, eller antall elever i en klasse rommet.

Kontinuerlige Tilfeldige Variabler:

Tilbake til myntkast, hva om vi ønsket å beskrive avstanden mellom der våre mynt kom til ro, og hvor den først traff bakken. Som avstand, x, ville være en kontinuerlig tilfeldig variabel fordi det kunne ta på et uendelig antall verdier i sammenhengende rekke av reelle tall., Mynten kunne reise 1 cm, eller 1,1 cm, eller 1.11 cm, eller av og på. Andre eksempler på kontinuerlige tilfeldige variabler ville være massen av stjerner i vår galakse, pH i havet farvann, eller botid i noen analytt i en gass chromatograph.

Blandet Tilfeldige Variabler:

Blandet tilfeldige variabler har både diskret og kontinuerlig komponenter. Slike tilfeldige variabler er sjelden forekommende. For et mulig eksempel, selv om du kan måle et eksempel på»s vekt, og bestemmer seg for at noen vekt, målt som en negativ verdi vil bli gitt en verdi på 0., På den måten vil den tilfeldige variabelen har en egen komponent i x = 0 og kontinuerlig komponent hvor x > 0.

Kumulativ Fordeling Funksjoner (CDF):

spørsmålet, selvfølgelig, dukker opp med hensyn til hvordan de best matematisk beskrive (og visuelt display) tilfeldige variabler. For de oppgaver vi bruker sannsynlighet tetthet funksjoner (PDF) og kumulativ tetthet funksjoner (CDF). Som CDFs er enklere å forstå for både diskrete og kontinuerlige tilfeldige variabler enn Pdf-filer, vil vi først forklare CDFs.

bør du Vurdere å kaste en rettferdig 6-sidded terninger., Vi ville ha en 1 i 6 sjanse til å få noen av de mulige verdiene av tilfeldig variabel (1, 2, 3, 4, 5, eller 6). Hvis vi plottet de mulige verdiene på x-aksen og plotte sannsynligheten for måling av hver bestemt verdi, x, eller en verdi som er mindre enn x på y-aksen, vil vi ha det CDF av tilfeldige variable.

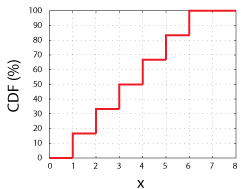
CDF for en Rettferdig 6-Sidded Terninger. Vær oppmerksom på at hvert trinn er på en høyde av 16.67%, eller 1 i 6.

Denne funksjonen, CDF(x), rett og slett forteller oss at oddsen for å måle hvilken som helst verdi opp til og med x., Som sådan, alle CDFs alle må ha disse egenskapene:

  1. EN CDF må være lik 0 når x = -∞, og tilnærmingen 1 (eller 100%) som x nærmer seg +∞. Enkelt sagt, ut av alle mulige utfall, må det være et utfall; sjansen for å kaste en seks-kantede terningen og får en verdi mellom -∞ og ∞ er 100%.
  2. skråningen av en CDF må alltid være lik eller større enn null. For eksempel, bør du vurdere sjansen for å kaste en 6-sidded terninger (virkelig eller ikke) og skaffe en verdi mellom 0 og 4., Den sjansen kan umulig være mer enn sjansen for å få en verdi mellom 0 og 5, fordi oddsen for en 1, 2 eller 3 landing med bildesiden opp er selvfølgelig alltid kommer til å være en brøkdel av oddsen for å få en 1, 2, 3, eller 4.

For et eksempel på en kontinuerlige tilfeldige variable, følgende appleten viser normalfordelt CDF.,div>

-5 5
x

This important distribution is discussed elsewhere., Bare vær oppmerksom på at egenskapene til en CDF er beskrevet ovenfor, og forklarte for en diskret tilfeldig variabel hold for kontinuerlige tilfeldige variabler, så vel.

For mer intuitiv eksempler på egenskaper av CDFs, se interaktiv eksempel nedenfor. Også, interaktive plott av mange andre CDFs viktig til feltet av statistikk og brukes på dette nettstedet kan bli funnet her.

Sannsynligheten Tetthet Funksjoner (PDF):

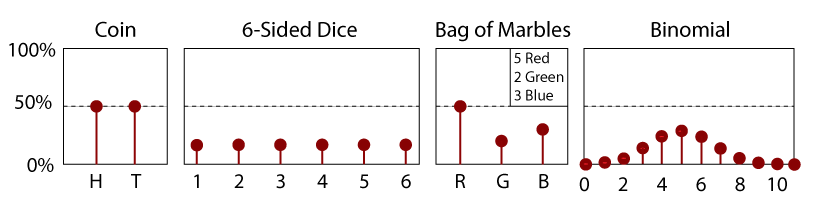
PDF for en Rettferdig 6-Sidded Terninger.

EN PDF-fil er rett og slett den deriverte av en CDF., Dermed en PDF-fil er også en funksjon av en tilfeldig variabel, x, og dens størrelse vil være noen indikasjon på den relative sannsynligheten for å måle en bestemt verdi. Som det er skråningen av en CDF, en PDF-fil må alltid være positiv, for det er ingen negative odds for enhver hendelse. Videre, og per definisjon, området under kurven av en PDF-fil(x) mellom -∞ og x er lik sin CDF(x). Som sådan, er området mellom to verdier x1 og x2 gir sannsynligheten for å måle en verdi i dette området.

følgende appleten viser et eksempel på PDF-filen for en normalfordelt tilfeldige variable, x.,

Normal PDF

mean:

stdev:

f(x):

x:

p
d
f		 0.,
-5 5
x

Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above.,

Også vurdere forskjellen mellom kontinuerlig og diskret PDF. Mens en diskret PDF (slik som vist over i terninger) vil gi deg oddsen for å oppnå et bestemt resultat, sannsynligheter med kontinuerlig Pdf-filer er spørsmål om utvalg, ikke diskrete punkter. For eksempel, det er helt klart en 1 i 6 (16.6%) sjanse for å rulle en 3 på en terning, som kan sees i sin PDF-fil. Men hva er oddsen for å måle nøyaktig null med en tilfeldig variabel har en normal PDF og betyr null, som vist ovenfor? Selv om det er den verdien der PDF-er størst, og sjansen for å måle nøyaktig 0.00000..,. er kanskje counter intuitivt, null. Oddsen for å måle noen bestemt tilfeldig nummer ut til uendelig presisjon er, faktisk, et null.

Med en kontinuerlig PDF-fil du kan i stedet spørre hva oddsen er at du vil måle mellom to verdier for å oppnå en sannsynlighet som er større enn null. For å finne denne sannsynligheten er vi rett og slett bruke det CDF av våre tilfeldig variabel., Fordi det CDF forteller oss at oddsen for å måle en verdi eller noe lavere enn denne verdien, for å finne sannsynligheten for å måle mellom to verdier, x1 og x2 (der x1 > x2) vi rett og slett nødt til å ta med verdien av det CDF på x1 og trekke fra verdien av CDF på x2. For eksempel, ved hjelp av normal CDF i applet ovenfor (med μ=0 og σ=1), hvis vi ønsket å vite oddsen for måling mellom 0,01 og 0,02 til vi finner CDF(x=0.1)=53.9828% og CDF(x=0.2)=57.9260%. Så forskjellen, CDF(0.2)-CDF(0.1), gir oss odds på ca 3,9% av måler en x mellom 0.1 og 0.2.,

For mer intuitive visuelle eksempler på egenskaper for Pdf-filer, se interaktiv eksempel nedenfor. Også, interaktive plott av mange viktige Pdf-filer som brukes på dette nettstedet kan sees her.

Legg igjen en kommentar

Din e-postadresse vil ikke bli publisert. Obligatoriske felt er merket med *