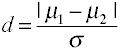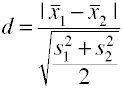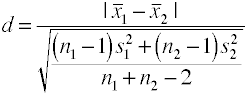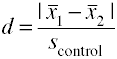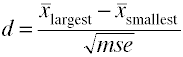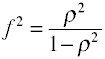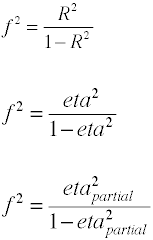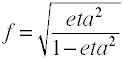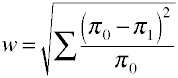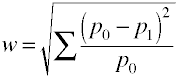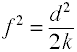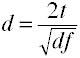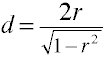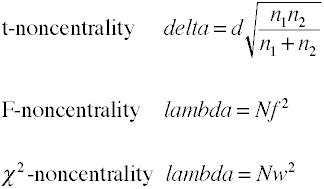Eén gebruik van effectgrootte is een gestandaardiseerde index die onafhankelijk is van de steekproefgrootte en de omvang van het verschil tussen populaties of de relatie tussen verklarende en responsvariabelen kwantificeert. Een ander gebruik van effect grootte is het gebruik ervan in het uitvoeren vanpower analyse.
effectgrootte voor verschil in gemiddelden
effectgrootte voor verschillen in gemiddelden wordt gegeven door de d van Cohen wordt gedefinieerd in termen van populatiegemiddelden (µs) en een populatiestandaarddeviatie (σ), zoals hieronder weergegeven.,
Er zijn verschillende manieren waarop men σ kan schatten aan de hand van steekproefgegevens die leiden tot meerdere varianten binnen de D-familie van Cohen.
gebruikmakend van de root mean square standaardafwijking
gebruikmakend van de gepoolde standaardafwijking (Hedges’ g)
deze versie van Cohen’ s d gebruikt de gepoolde standaardafwijking en is ook bekend als heggen ” g.,
u kunt deze waarde eenvoudig uit een anova-programma verkrijgen door de vierkantswortel van de meansquare-fout te nemen, die ook bekend staat als de root mean square-fout.
met behulp van de controlegroep standaardafwijking (glas’ Δ)
een andere versie van Cohen’ s d met behulp van de standaardafwijking voor de controlegroep wordt ook wel glas ‘ Δ genoemd.,
meer dan twee groepen
wanneer er meer dan twee groepen zijn, gebruiken we het verschil tussen de grootste en de kleinste waarde gedeeld door de vierkantswortel van de gemiddelde vierkantfout.
effectgrootte voor F-ratio ‘ s in regressieanalyse
voor OLS-regressie is de maat voor effectgrootte F, die door Cohen als volgt wordt gedefinieerd.,
opnieuw zijn er verschillende manieren waarop de effectgrootte kan worden berekend uit voorbeeldgegevens. Merk op dat η2 een andere naam is voor R2.
effectgrootte voor F-ratio ‘ s in variantieanalyse
de effectgrootte die wordt gebruikt bij variantieanalyse wordt gedefinieerd door de ratio van populatiestandaarddeviaties.,
hoewel Cohen ‘ s f als hierboven is gedefinieerd, wordt deze meestal berekend door de vierkantswortel van f2 te nemen.
effectgrootte voor χ2 uit contingency tables
opnieuw beginnen we met de definitieformule in termen van populatiewaarden.Effectgrootte w is de vierkantswortel van de gestandaardiseerde chi-kwadraatstatistiek.,
en zo wordt W berekend met behulp van voorbeeldgegevens.
Hier is een tabel met voorgestelde waarden voor lage, gemiddelde en hoge effecten (Cohen, 1988). Deze waarden mogen niet als absoluut worden beschouwd en moeten worden geïnterpreteerd binnen de context van uw onderzoeksprogramma. De waarden voor grote effecten worden vaak overschreden in de praktijk met waarden Cohen ‘ s d groter dan 1,0 niet ongewoon.,Echter, met behulp van zeer grote effect maten in prospectieve power analyse is waarschijnlijk niet een goed idee asit zou kunnen leiden tot onder aangedreven studies.,formules
waar k = aantal groepen
Converteren t tot d voor twee onafhankelijke groepen
Converteren r d voor twee onafhankelijke groepen
Noncentrality schattingen
Power-analyse met behulp van analytische methoden vereisen een schatting van noncentrality die basicallythe effect grootte vermenigvuldigd met een sample size factor., Hier zijn enkele formules voor het schatten van noncentraliteit.
voorbeeld vermogensanalyse
Hier is een voorbeeld dat effectgrootte en niet-centraliteit samenbrengt in een vermogensanalyse.
overweeg een eenrichtingsanalyse van variantie met drie groepen (k = 3). Als we verwachten dat andeta2 gelijk is .,12 in dat geval zal de effectgrootte
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
bij een geprojecteerde steekproefgrootte van 60 is de schatting van niet-centraliteit
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
De teller vrijheidsgraden is k-1 = 3-1 = 2 terwijl de noemer df N-k = 60-3 = 57 is.De kritische waarde van F met 2 en 57 vrijheidsgraden is 3,16. Wat resulteert in een macht van
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
dus een n van 60 en effectgrootte van.369 levert een geprojecteerde kracht van ongeveer .7.
We kunnen de kracht van verbeteren .7 door gebruik te maken van een geprojecteerde steekproefgrootte van 75 in plaats van 60., Met dezelfde effectgrootte van.369, krijgen we een nieuwe niet-centraliteitsschatting van
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
De teller vrijheidsgraden blijven hetzelfde terwijl de noemer df nu gelijk is aan N-k = 75-3 = 72.De kritische waarde van F met 2 en 72 vrijheidsgraden van 3,12. Deze keer is het vermogen
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
wat binnen aanvaardbare onderzoekslimieten ligt.
merk op dat verschillende stat-pakketten verschillende namen en een andere volgorde van argumenten gebruiken in de functie die we noncentralFtail noemen. U moet de documentatie lezen die met uw software wordt geleverd.,
Becker, L. Psychologie 590 course notes. Bekeken 19 Jun 2009 <http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen, J. 1988. Statistische vermogensanalyse voor de gedragswetenschappen. Hillsdale, New Jersey: Lawrence Erlbaum Associates