de regels die bepalen hoe gehele getallen te vermenigvuldigen en te delen zijn zeer vergelijkbaar. In deze les zullen we ons richten op de vermenigvuldiging van gehele getallen.
regels over het vermenigvuldigen van gehele getallen
Stap 1: vermenigvuldig hun absolute waarden.
Stap 2: Bepaal het teken van het uiteindelijke antwoord (in dit geval wordt het het product genoemd omdat we vermenigvuldigen) onder de volgende voorwaarden.
- Voorwaarde 1: als de tekenen van de twee getallen hetzelfde zijn, is het product altijd een positief getal.,
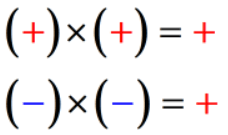
- voorwaarde 2: als de tekenen van de twee getallen verschillen, is het product altijd een negatief getal.
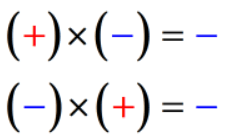
voorbeelden van gehele getallen
Voorbeeld 1: vermenigvuldig de gehele getallen hieronder.
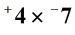
oplossing: haal eerst de absolute waarde van elk getal.,
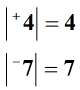
vermenigvuldig of zoek het product van de absolute waarden.
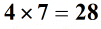
bepaal ten slotte het teken van het definitieve antwoord. De regel stelt dat als de tekens van de twee gehele getallen verschillend zijn, het uiteindelijke antwoord negatief zal zijn.
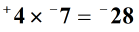
Voorbeeld 2: vermenigvuldig de gehele getallen hieronder.,
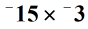
oplossing: vermenigvuldig de absolute waarden van de twee getallen.
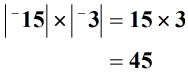
aangezien we gehele getallen met hetzelfde teken vermenigvuldigen, moet het uiteindelijke antwoord (product) positief zijn.
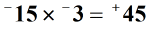
Voorbeeld 3: Zoek het product van de drie gehele getallen hieronder.,
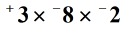
oplossing: we kunnen ook drie of meer gehele getallen vermenigvuldigen. We hoeven alleen maar twee gehele getallen tegelijk te vermenigvuldigen. Laat me een haakje plaatsen om aan te geven welke twee getallen we eerst gaan vermenigvuldigen. Het product van + 3 en -8 is gelijk aan-24. Het is negatief omdat de tekens anders zijn. Vermenigvuldig dan-24 bij -2 om +48 te krijgen. Onthoud, het product van twee gehele getallen met hetzelfde teken is altijd positief.,
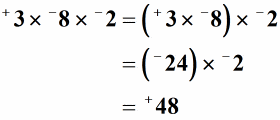
oefen met werkbladen
u bent wellicht ook geïnteresseerd in:
gehele optelling
gehele aftrekking
integer deling