De α-coëfficiënt is de meest gebruikte procedure voor het schatten van betrouwbaarheid in toegepast onderzoek. Zoals Sijtsma (2009) stelt, is zijn populariteit zodanig dat Cronbach (1951) vaker als referentie wordt aangehaald dan het artikel over de ontdekking van de DNA-dubbele helix., Niettemin zijn de beperkingen ervan bekend (Lord and Novick, 1968; Cortina, 1993; Yang and Green, 2011), Enkele van de belangrijkste zijn de veronderstellingen van ongecorreleerde fouten, Tau-equivalentie en normaliteit.
the assumption of uncorrelated errors (the error score of any pair of items is uncorrelated) is a hypothesis of Classical Test Theory (Lord and Novick, 1968), violation of which may imply the presence of complex multidimensional structures required estimation procedures which account this complexity including (e.g. Tarkkonen and Vehkalahti, 2005; Green And Yang, 2015)., Het is belangrijk om de onjuiste overtuiging dat de α-coëfficiënt een goede indicator is voor de unidimensionaliteit uit de wereld te helpen, omdat de waarde ervan hoger zou zijn als de schaal eendimensionaal zou zijn. In feite is precies het tegenovergestelde het geval, zoals werd aangetoond door Sijtsma (2009), en de toepassing ervan in dergelijke omstandigheden kan leiden tot een zwaar overschatting van de betrouwbaarheid (Raykov, 2001). Daarom moet voor de berekening van α worden nagegaan of de gegevens in eendimensionale modellen passen.
de aanname van Tau-equivalentie (d.w.z.,, dezelfde werkelijke score voor alle testitems, of gelijke factorbelasting van alle items in een factormodel) is een vereiste voor α om gelijkwaardig te zijn aan de betrouwbaarheidscoëfficiënt (Cronbach, 1951). Als de aanname van Tau-equivalentie wordt geschonden, zal de werkelijke betrouwbaarheidswaarde worden onderschat (Raykov, 1997; Graham, 2006) met een bedrag dat kan variëren tussen 0,6 en 11,1% afhankelijk van de ernst van de overtreding (Green And Yang, 2009a). Werken met gegevens die aan deze aanname voldoen is over het algemeen niet haalbaar in de praktijk (Teo and Fan, 2013); het congeneric model (I. E.,, verschillende factor belastingen) is de meer realistische.
de eis voor multivariante normaliteit is minder bekend en beïnvloedt zowel de puntuele betrouwbaarheidsschatting als de mogelijkheid om betrouwbaarheidsintervallen vast te stellen (Dunn et al., 2014). Sheng and Sheng (2012) merkte onlangs op dat wanneer de verdelingen scheef en/of leptokurtisch zijn, een negatieve bias wordt geproduceerd wanneer de coëfficiënt α wordt berekend; vergelijkbare resultaten werden gepresenteerd door Green And Yang (2009b) in een analyse van de effecten van niet-normale verdelingen bij het schatten van betrouwbaarheid., Studie van Scheve problemen is belangrijker als we zien dat in de praktijk onderzoekers gewoonlijk werken met schuine schalen (Micceri, 1989; Norton et al., 2013; Ho and Yu, 2014). Bijvoorbeeld, Micceri (1989) schatte dat ongeveer 2/3 van het vermogen en meer dan 4/5 van de psychometrische metingen vertoonde ten minste matige asymmetrie (dat wil zeggen, scheefheid rond 1). Ondanks dit, is de impact van scheefheid op de schatting van de betrouwbaarheid weinig onderzocht.,gezien de overvloedige literatuur over de beperkingen en vooroordelen van de α-coëfficiënt (Revelle and Zinbarg, 2009; Sijtsma, 2009, 2012; Cho and Kim, 2015; Sijtsma and Van der Ark, 2015), rijst de vraag waarom onderzoekers α blijven gebruiken wanneer er alternatieve coëfficiënten bestaan die deze beperkingen overwinnen. Het is mogelijk dat de overmaat aan procedures voor het schatten van betrouwbaarheid die in de vorige eeuw is ontwikkeld, het debat heeft doen wankelen. Dit zou nog worden verergerd door de eenvoud van het berekenen van deze coëfficiënt en de beschikbaarheid ervan in commerciële software.,
de moeilijkheid om de PXX “betrouwbaarheidscoëfficiënt ligt in zijn definitie pxx” =σt2 σ σx2 te schatten, die de werkelijke score in de variantie-teller omvat wanneer deze van nature niet waarneembaar is. De α-coëfficiënt probeert deze niet waarneembare afwijking van de covariantie tussen de items of componenten te benaderen. Cronbach (1951) toonde aan dat bij afwezigheid van Tau-equivalentie De α-coëfficiënt (of Guttman”s lambda 3, die gelijk is aan α) een goede ondergrens benadering was., Wanneer de veronderstellingen dus worden geschonden, vertaalt het probleem zich in het vinden van de best mogelijke ondergrens; inderdaad wordt deze naam gegeven aan de grootste ondergrens methode (GLB) die de best mogelijke benadering is vanuit een theoretische hoek (Jackson en Agunwamba, 1977; Woodhouse en Jackson, 1977; Shapiro en ten Berge, 2000; Sočan, 2000; ten Berge en Sočan, 2004; Sijtsma, 2009). Revelle en Zinbarg (2009) zijn echter van mening dat ω een betere ondergrens geeft dan GLB., Er is dus een open discussie over de vraag welke van deze twee methoden de beste ondergrens geeft; bovendien is de kwestie van niet-normaliteit niet uitputtend onderzocht, zoals in dit werk wordt besproken.
ω-coëfficiënten
McDonald (1999) stelde de wt-coëfficiënt voor het schatten van de betrouwbaarheid voor uit een factorieel analysekader, dat formeel kan worden uitgedrukt als:
waar λj de belasting van item j is, λj2 de gemeenschappelijkheid van item j is en ψ gelijk is aan de uniciteit., De WT-coëfficiënt, door de lambda ‘ s in zijn formules op te nemen, is geschikt zowel wanneer Tau-equivalentie (d.w.z. gelijke factorbelasting van alle testitems) bestaat (wt valt wiskundig samen met α), als wanneer items met verschillende discriminaties aanwezig zijn in de representatie van de constructie (d.w.z. verschillende factorbelasting van de items: congenere metingen). Bijgevolg corrigeert wt de onderschatting van α wanneer de aanname van Tau-equivalentie wordt geschonden (Dunn et al., 2014) en verschillende studies tonen aan dat het een van de beste alternatieven is voor het schatten van betrouwbaarheid (Zinbarg et al.,, 2005, 2006; Revelle and Zinbarg, 2009), hoewel tot op heden de werking ervan in scheefheid niet bekend is.
wanneer er correlatie bestaat tussen fouten, of er meer dan één latente dimensie in de gegevens is, wordt de bijdrage van elke dimensie aan de totale variantie geschat, waarbij de zogenaamde hiërarchische ω (wh) wordt verkregen die ons in staat stelt om de ergste overschatting bias van α met multidimensionale gegevens te corrigeren (zie Tarkkonen en Vehkalahti, 2005; Zinbarg et al., 2005; Revelle and Zinbarg, 2009)., Coëfficiënten wh en wt zijn equivalent in unidimensionale gegevens, dus we zullen verwijzen naar deze coëfficiënt gewoon als ω.
Greatest Lower Bound (GLB)
Sijtsma (2009) toont in een reeks studies aan dat een van de krachtigste schatters van betrouwbaarheid GLB—afgeleid door Woodhouse and Jackson (1977) uit de aannames van de klassieke Testtheorie (Cx = Ct + Ce)—een inter-item covariantiematrix voor waargenomen itemscores Cx. Het bestaat uit twee delen: de som van de inter-item covariantie matrix voor item true scores Ct; en de inter-item error covariance matrix Ce (ten Berge and Sočan, 2004)., De uitdrukking is:
waarbij σx2 de testvariantie is en tr (Ce) verwijst naar het spoor van de covariantiematrix tussen items die zo moeilijk te schatten is. Een oplossing is geweest om factoriële procedures zoals Minimum Rank Factor analyse (een procedure bekend als glb.fa). Meer recent is de GLB algebraïsche (GLBa) procedure ontwikkeld op basis van een algoritme bedacht door Andreas Moltner (Moltner and Revelle, 2015)., Volgens Revelle (2015a) neemt deze procedure de vorm aan die het meest trouw is aan de oorspronkelijke definitie van Jackson en Agunwamba (1977), en heeft het extra voordeel dat het een vector invoert om de items op gewicht te wegen (Al-Homidan, 2008).
ondanks zijn theoretische sterke punten is GLB zeer weinig gebruikt, hoewel enkele recente empirische studies hebben aangetoond dat deze coëfficiënt betere resultaten oplevert dan α (Lila et al., 2014) en α En ω (Wilcox et al., 2014)., Niettemin, in kleine steekproeven, onder de aanname van normaliteit, neigt het om de ware betrouwbaarheidswaarde te overschatten (Shapiro en ten Berge, 2000); nochtans blijft het functioneren onder niet-normale omstandigheden onbekend, met name wanneer de verdelingen van de items asymmetrisch zijn.
rekening houdend met de hierboven gedefinieerde coëfficiënten en de vooroordelen en beperkingen van elk daarvan, is het doel van deze werkzaamheden de robuustheid van deze coëfficiënten te evalueren in aanwezigheid van asymmetrische elementen, rekening houdend met de aanname van Tau-equivalentie en de steekproefgrootte.,
Methodes
het Genereren van Gegevens
De gegevens zijn gegenereerd met behulp van R (R Development Core Team, 2013) en RStudio (Racine, 2012) software, het volgen van de faculteit model:
waar Xij is de gesimuleerde reactie van het onderwerp dat ik in punt j, λjk is het laden van item j in Factor k (die werd gegenereerd door de unifactorial model); Fk is de latente factor gegenereerd door een standaard normale verdeling (gemiddelde 0 en variantie 1), en ej is de willekeurige meetfout van elk item ook het volgen van een standaard normale verdeling.,
Scheve items: Standaard normale Xij werden omgevormd tot het genereren van niet-normale verdelingen met behulp van de procedure voorgesteld door Headrick (2002) het toepassen van de vijfde orde polynoom verandert:
Gesimuleerde Voorwaarden
Voor het beoordelen van de prestaties van de betrouwbaarheid van de coëfficiënten (α, ω, GLB en GLBa) we werkten met drie steekproeven (250, 500, 1000), twee test maten: klein (6 items) en lange (12 items), twee voorwaarden van tau-equivalentie (één met tau-equivalentie en één zonder, d.w.z. de,, congeneric) en de progressieve integratie van asymmetrische items (van alle items zijn normaal tot alle items zijn asymmetrisch). In de korte proef werd de betrouwbaarheid vastgesteld op 0,731, hetgeen in aanwezigheid van Tau-equivalentie wordt bereikt met zes punten met factorbelasting = 0,558; terwijl het congenere model wordt verkregen door factorbelasting in te stellen op waarden van 0.3, 0.4, 0.5, 0.6, 0.7, en 0.8 (Zie bijlage I). In de lange test van 12 items werd de betrouwbaarheid ingesteld op 0.,845 met dezelfde waarden als in de korte test voor zowel Tau-equivalentie als het congenerische model (in dit geval waren er twee items voor elke waarde van lambda). Op deze manier werden 120 condities gesimuleerd met 1000 replica ‘ s in elk geval.
Data-analyse
de belangrijkste analyses werden uitgevoerd met behulp van de psych (Revelle, 2015b) en Gparotatie (Bernaards en Jennrich, 2015) pakketten, waarmee α en ω kunnen worden geschat. Voor het schatten van GLB werden twee geautomatiseerde benaderingen gebruikt: glb.fa (Revelle, 2015a) en glb.,algebraïsch (Moltner and Revelle, 2015), de laatste werkte door auteurs als Hunt and Bentler (2015).
om de nauwkeurigheid van de verschillende schatters in het herstellen van betrouwbaarheid te evalueren, hebben we het Root Mean Square of Error (RMSE) en de bias berekend. De eerste is het gemiddelde van de verschillen tussen de geschatte en de gesimuleerde betrouwbaarheid en wordt geformaliseerd als:
waarbij ρ^ de geschatte betrouwbaarheid voor elke coëfficiënt is, ρ de gesimuleerde betrouwbaarheid en Nr het aantal replica ‘ s., De % bias wordt begrepen als het verschil tussen het gemiddelde van de geschatte betrouwbaarheid en de gesimuleerde betrouwbaarheid en wordt gedefinieerd als:
In beide indices, hoe groter de waarde, hoe groter de onnauwkeurigheid van de schatter, maar in tegenstelling tot RMSE, kan de bias positief of negatief zijn; in dit geval wordt aanvullende informatie verkregen over de vraag of de coëfficiënt de gesimuleerde betrouwbaarheidsparameter onderschat of overschat., Op aanbeveling van Hoogland en Boomsma (1998) werden waarden van RMSE < 0,05 en % bias < 5% aanvaardbaar geacht.
resultaten
de belangrijkste resultaten zijn te zien in Tabel 1 (6 items) en Tabel 2 (12 items). Deze tonen de RMSE en % bias van de coëfficiënten in Tau-equivalentie en congeneric Voorwaarden, en hoe de scheefheid van de testverdeling toeneemt met de geleidelijke integratie van asymmetrische items.
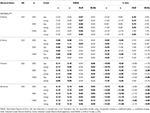
Tabel 1., RMSE en Bias met Tau-equivalentie en congeneric conditie voor 6 items, drie Monster maten en het aantal scheef items.
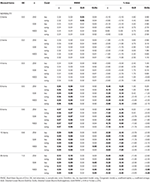
Tabel 2. RMSE en Bias met Tau-equivalentie en congeneric conditie voor 12 items, drie Monster maten en het aantal scheef items.
alleen onder voorwaarden van Tau-equivalentie en normaliteit (scheefheid < 0,2) wordt waargenomen dat de α-Coëfficiënt De gesimuleerde betrouwbaarheid correct schat, zoals ω., In congeneren corrigeert ω de onderschatting van α. Zowel GLB als GLBa vertonen een positieve bias onder normale omstandigheden, maar GLBa vertoont ongeveer ½ % minder bias dan GLB (zie Tabel 1). Als we kijken naar de steekproefgrootte, zien we dat als de testgrootte toeneemt, de positieve bias van GLB en GLBa afneemt, maar nooit verdwijnt.
in asymmetrische omstandigheden zien we in Tabel 1 dat zowel α als ω een onaanvaardbare prestatie vertonen met toenemende RMSE en onderschattingen die bias > 13% kunnen bereiken voor de α-coëfficiënt (tussen 1 en 2% lager voor ω)., De GLB-en GLBa-coëfficiënten geven een lagere RMSE wanneer de test scheef is of het aantal asymmetrische items toeneemt (zie tabellen 1 en 2). De GLB-coëfficiënt geeft betere schattingen wanneer de test scheefheidswaarde van de test rond 0,30 is; GLBa is zeer vergelijkbaar, met betere schattingen Dan ω met een test scheefheidswaarde rond 0,20 of 0,30. Echter, wanneer de scheefheid waarde stijgt tot 0,50 of 0,60, GLB presenteert betere prestaties dan GLBa. De testomvang (6 of 12 punten) heeft een veel belangrijker effect dan de steekproefomvang op de nauwkeurigheid van de schattingen.,
discussie
in deze studie werden vier factoren gemanipuleerd: Tau-equivalentie of congenerisch model, steekproefgrootte (250, 500, en 1000), het aantal testpunten (6 en 12) en het aantal asymmetrische items (van 0 asymmetrische items tot alle items die asymmetrisch zijn) om de robuustheid te evalueren ten opzichte van de aanwezigheid van asymmetrische gegevens in de vier geanalyseerde betrouwbaarheidscoëfficiënten. Deze resultaten worden hieronder besproken.,
bij Tau-equivalentie convergeren de α-En ω-coëfficiënten, maar bij afwezigheid van Tau-equivalentie (congeneer) geeft ω altijd betere schattingen en kleinere RMSE-en % – bias Dan α. In deze meer realistische toestand (Green And Yang, 2009a; Yang and Green, 2011) wordt α een negatief bevooroordeelde betrouwbaarheids-estimator (Graham, 2006; Sijtsma, 2009; Cho and Kim, 2015) en ω heeft altijd de voorkeur boven α (Dunn et al., 2014). In het geval van niet-schending van de aanname van normaliteit, ω is de beste schatter van alle beoordeelde coëfficiënten (Revelle en Zinbarg, 2009).,
wat de steekproefgrootte betreft, merken we op dat deze factor een klein effect heeft bij normaliteit of een lichte afwijking van normaliteit: de RMSE en de bias nemen af naarmate de steekproefgrootte toeneemt. Niettemin kan worden gezegd dat Voor deze twee coëfficiënten, met steekproefgrootte van 250 en normaliteit verkrijgen we relatief nauwkeurige schattingen (Tang and Cui, 2012; Javali et al., 2011)., Voor de GLB en GLBa coëfficiënten, als de steekproefgrootte verhoogt de RMSE en de bias de neiging om te verminderen; maar ze handhaven een positieve bias voor de toestand van normaliteit, zelfs met grote steekproefgrootte van 1000 (Shapiro en ten Berge, 2000; ten Berge en Sočan, 2004; Sijtsma, 2009).
voor de testgrootte zien we in het algemeen een hogere RMSE en bias met 6 items dan met 12, wat suggereert dat hoe hoger het aantal items, hoe lager de RMSE en de bias van de schatters (Cortina, 1993). Over het algemeen wordt de trend voor zowel 6 als 12 items gehandhaafd.,
wanneer we kijken naar het effect van het geleidelijk opnemen van asymmetrische items in de gegevensverzameling, zien we dat de α-coëfficiënt zeer gevoelig is voor asymmetrische items; deze resultaten zijn vergelijkbaar met die gevonden door Sheng and Sheng (2012) en Green And Yang (2009b). De coëfficiënt ω vertoont vergelijkbare RMSE-en bias-waarden als die van α, maar iets beter, zelfs bij Tau-equivalentie. GLB en GLBa zijn gevonden om betere schattingen te presenteren wanneer de test scheefheid afwijkt van waarden dicht bij 0.
Overwegende dat het in de praktijk gebruikelijk is om asymmetrische gegevens te vinden (Micceri, 1989; Norton et al.,, 2013; Ho en Yu, 2014), Sijtsma ” s suggestie (2009) van het gebruik van GLB als een betrouwbaarheid estimator lijkt goed gefundeerd. Andere auteurs, zoals Revelle and Zinbarg (2009) en Green And Yang (2009a), bevelen het gebruik van ω aan, maar deze coëfficiënt leverde alleen goede resultaten op in de toestand van normaliteit, of met een laag aandeel van scheefheidsitems. Deze coëfficiënten leverden in ieder geval Grotere theoretische en empirische voordelen op dan α. Niettemin raden we onderzoekers aan om niet alleen punctuele schattingen te bestuderen, maar ook om gebruik te maken van interval schatting (Dunn et al., 2014).,
Deze resultaten zijn beperkt tot de gesimuleerde omstandigheden en er wordt aangenomen dat er geen correlatie tussen fouten is. Dit zou het noodzakelijk maken om verder onderzoek uit te voeren naar de werking van de verschillende betrouwbaarheidscoëfficiënten met complexere multidimensionale structuren (Reise, 2012; Green And Yang, 2015) en in de aanwezigheid van ordinale en/of categorische gegevens waarin niet-naleving van de aanname van normaliteit de norm is.
conclusie
wanneer de totale testscores normaal worden verdeeld (d.w.z., de eerste keuze zou moeten zijn, gevolgd door α, omdat zij de overschatting van GLB voorkomen. Echter, wanneer er een lage of matige test scheefheid GLBa moet worden gebruikt. GLB wordt aanbevolen wanneer het aandeel asymmetrische elementen hoog is, aangezien onder deze omstandigheden het gebruik van zowel α Als ω als betrouwbaarheidsinschatting, ongeacht de steekproefgrootte, niet aan te raden is.
Auteursbijdragen
ontwikkeling van het idee van onderzoek en theoretisch kader (IT, JA). Opbouw van het methodologisch kader (IT, JA)., Ontwikkeling van de R taal syntaxis (IT, JA). Gegevensanalyse en interpretatie van gegevens (IT, JA). Bespreking van de resultaten in het licht van de huidige theoretische achtergrond (Ja, IT). Voorbereiding en schrijven van het artikel (Ja, IT). In het algemeen hebben beide auteurs in gelijke mate bijgedragen aan de ontwikkeling van dit werk.,
financiering
De eerste auteur maakte de ontvangst bekend van de volgende financiële steun voor het onderzoek, het auteurschap en / of de publicatie van dit artikel: hij ontving financiële steun van de Chileense nationale commissie voor Wetenschappelijk en Technologisch Onderzoek (CONICYT) “Becas Chile” Doctoral Fellowship program (Grant no: 72140548).
belangenconflict verklaring
De auteurs verklaren dat het onderzoek werd uitgevoerd zonder enige commerciële of financiële relatie die als een potentieel belangenconflict kon worden opgevat.
Cronbach, L. (1951)., Coëfficiënt alfa en de interne structuur van de tests. Psychometrika 16, 297-334. doi: 10.1007 / BF02310555
CrossRef Full Text / Google Scholar
McDonald, R. (1999). Test theorie: een uniforme behandeling. Mahwah, NJ: Lawrence Erlbaum Associates.
Google Scholar
R Development Core Team (2013). R: een taal en omgeving voor statistische gegevensverwerking. Wenen: R Stichting statistische Informatica.
Raykov, T. (1997)., Scale reliability, cronbach”s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package “psych.,”Available online at: http://org/r/psych-manual.pdf
Shapiro, A., and ten Berge, J. M. F. (2000). De asymptotische bias van minimale sporenfactoranalyse, met toepassingen tot de grootste ondergrens van betrouwbaarheid. Psychometrika 65, 413-425. doi: 10.1007 / BF02296154
CrossRef Full Text / Google Scholar
ten Berge, J. M. F., and Sočan, G. (2004). De grootste ondergrens aan de betrouwbaarheid van een test en de hypothese van unidimensionaliteit. Psychometrika 69, 613-625. doi: 10.,1007 / BF02289858
CrossRef Full Text / Google Scholar
Woodhouse, B., and Jackson, P. H. (1977). Ondergrenzen voor de betrouwbaarheid van de totale score bij een test die bestaat uit niet-homogene items: II: een zoekprocedure om de grootste ondergrens te bepalen. Psychometrika 42, 579-591. doi: 10.1007 / BF02295980
CrossRef Full Text / Google Scholar
Appendix I
R syntaxis om betrouwbaarheidscoëfficiënten uit Pearson ‘ s correlatiematrices te schatten., De correlatiewaarden buiten de diagonaal worden berekend door de factorbelasting van de items te vermenigvuldigen: (1) Tau-equivalent model ze zijn allemaal gelijk aan 0,3114 (λiλj = 0,558 × 0,558 = 0,3114) en (2) congeneer model ze variëren als functie van de verschillende factorbelasting (bijvoorbeeld het matrixelement a1, 2 = λ1λ2 = 0,3 × 0,4 = 0,12). In beide voorbeelden is de werkelijke betrouwbaarheid 0,731.
> Omega(Cr,1)$alpha # standardized Cronbach ” s α
0,731
> Omega(Cr,1)$omega.tot # coëfficiënt ω totaal
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach”s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731