een regressiemodel voor Overlevingsdata
Ik schreef eerder over het berekenen van de Kaplan–Meier curve voor overlevingsdata. Als een niet-parametrische schatter, het doet een goed werk van het geven van een snelle blik op de survival curve voor een dataset. Echter, wat het je niet laat doen is het model van de impact van covarianten op overleving. In dit artikel zullen we ons richten op het Cox Proportional Hazards model, een van de meest gebruikte modellen voor overlevingsdata.
We gaan dieper in op het berekenen van de schattingen., Dit is waardevol omdat we zullen zien dat de schattingen alleen afhangen van de volgorde van fouten en niet van hun werkelijke tijden. We zullen ook kort enkele lastige kwesties bespreken over causale gevolgtrekking die speciaal zijn voor overlevingsanalyse.
we denken meestal over overlevingsdata in termen van overlevingscurven zoals hieronder.,
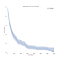
op de x-as hebben we de tijd in dagen. Op de y-as, hebben we (een schatter voor) het percentage (technisch, proportie) van proefpersonen in de populatie die “overleven” tot die tijd. Overleven kan figuurlijk of letterlijk zijn., Het zou kunnen zijn of mensen een bepaalde leeftijd bereiken, of een machine het een bepaalde tijd maakt zonder af te breken, of het zou kunnen zijn of iemand een bepaalde tijd werkloos blijft na het verliezen van zijn baan.
cruciaal is dat de complicatie in overlevingsanalyse is dat bij sommige proefpersonen hun “dood” niet is waargenomen. Ze kunnen nog in leven zijn, een machine kan nog steeds functioneren, of iemand kan nog steeds werkloos zijn op het moment dat de gegevens worden verzameld., Dergelijke observaties worden “rechts-gecensureerd” genoemd en het omgaan met censuur betekent dat survival analyse verschillende statistische instrumenten vereist.
We geven de overlevende functie aan als S, een functie van de tijd. De output is het percentage proefpersonen dat overleeft op tijd t. (nogmaals, het is technisch een verhouding tussen 0 en 1, maar Ik zal de twee woorden door elkaar gebruiken). Voor de eenvoud zullen we de technische aanname maken dat als we lang genoeg wachten, alle onderwerpen zullen “sterven.”
We zullen de onderwerpen indexeren met een subscript zoals i of j., Het falen keer van de hele bevolking, wordt dit aangegeven met een vergelijkbare subscript op de variabele tijd t.

Een andere subtiliteit is om te overwegen is of we de behandeling van de tijd als discrete (van week tot week, zeggen) of continu. Filosofisch gesproken meten we de tijd alleen in discrete stappen (tot op de dichtstbijzijnde seconde, zeg maar)., Gewoonlijk vertellen onze gegevens ons alleen of iemand in een bepaald jaar is overleden of dat een machine op een bepaalde dag uitvalt. Ik zal heen en weer gaan tussen de discrete en continue gevallen in het belang van het houden van de uiteenzetting zo duidelijk mogelijk.
wanneer we proberen de effecten van covariabelen (bijvoorbeeld leeftijd, geslacht, ras, machinefabrikant) te modelleren, zullen we doorgaans geïnteresseerd zijn in het begrijpen van het effect van de covariabele op de Gevarenratio. De gevarenratio is de momentane kans op falen/overlijden/toestandstransitie op een bepaald tijdstip t, afhankelijk van het feit dat ze al zo lang hebben overleefd., We zullen het λ(t) aanduiden. Tijd als discreet behandelen:
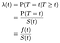
waarbij f de totale kansdichtheid van falen is op tijdstip t. we kunnen de discrete en continue gevallen verenigen door deltafuncties toe te staan in de kansdichtheid “functie”. Het resultaat λ = f / S is dus hetzelfde voor het continue geval.
laten we een voorbeeld repareren., Laten we eens kijken naar de context van een klinische proef waarbij een medicijn in eerste instantie zorgt dat een ziekte in remissie gaat. We zullen zeggen dat het medicijn “mislukt” voor een onderwerp wanneer de ziekte voor een onderwerp begint te vorderen. Ten slotte, stel dat de ziektestatus van proefpersonen elke week wordt gemeten. Dan als λ (3) = 0,1, dat betekent dat er een 10% kans dat, Voor een bepaald onderwerp, als ze nog steeds in remissie vóór week 3, hun ziekte zal beginnen te vorderen in week 3. De overige 90% blijft in remissie.,
Vervolgens is de Algemene kansdichtheidsfunctie f gewoon de afgeleide van S met betrekking tot tijd. (Nogmaals, als de tijd discreet is, is f gewoon de som van sommige deltafuncties).,341fa8b2″>
Dit betekent dat als we weten dat de Hazard-functie, kunnen we het oplossen van deze differentiaalvergelijking voor S:
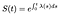
Als de tijd is discreet, de integraal van een som van delta functies gewoon verandert in een som van de risico ‘ s op elke discrete tijd.,
Oké, dat vat de notatie en basisconcepten samen die we nodig zullen hebben. Laten we verder gaan met het bespreken van modellen.
niet-, Semi-en volledig-parametrische modellen
zoals ik al eerder zei, zijn we meestal geïnteresseerd in het modelleren van de Hazard Rate λ.
in een niet-parametrisch model maken we geen aannames over de functionele vorm van λ. De Kaplan-Meier-Curve is in dit geval de maximale Waarschijnlijkheidsschatting. Het nadeel is dat dit het moeilijk maakt om effecten van covariaten te modelleren. Het is een beetje als het gebruik van een scatter plot om het effect van een covariant te begrijpen., Niet per se zo nuttig als een volledig parametrisch model zoals een lineaire regressie.
in een volledig parametrisch model maken we een aanname voor de precieze functionele vorm van λ. Een bespreking van de volledig parametrische modellen is een volledig artikel op zich, maar het is de moeite waard een zeer korte discussie. De onderstaande tabel toont drie van de meest voorkomende volledig parametrische modellen. Elk wordt gegeneraliseerd door de volgende, gaande van 1 tot 2 tot 3 parameters. De functionele vorm voor de gevarenfunctie wordt weergegeven in de middelste kolom. De logaritme van de gevarenfunctie wordt ook weergegeven in de laatste kolom., Alle parameters (ɣ, α, μ) worden verondersteld positief te zijn, behalve dat μ 0 zou kunnen zijn in de gegeneraliseerde Weibull-verdeling (die de Weibull-verdeling reproduceert).

als we naar de logaritme kijken, zien we dat het exponentiële model ervan uitgaat dat de hazard-functie constant is. Het Weibull-model gaat ervan uit dat het toeneemt als α>1, constant Als α=1, en afneemt als α<1., Het gegeneraliseerde Weibull model begint op dezelfde manier als het Weibull model (aan het begin ln S = 0). Daarna komt er een extra term μ.
het probleem met deze modellen is dat ze sterke veronderstellingen maken over de gegevens. In bepaalde contexten, kunnen er redenen zijn om te geloven dat deze modellen zijn een goede pasvorm. Maar met deze en verschillende andere opties die beschikbaar zijn, is er een groot risico op het trekken van onjuiste conclusies als gevolg van een verkeerde specificatie van het model.
daarom is het Cox Proportional Hazards, een semi-parametrisch model zo populair., Er worden geen functionele veronderstellingen gemaakt over de vorm van de gevarenfunctie; in plaats daarvan worden functionele-vorm veronderstellingen gemaakt over de effecten van de covarianten alleen.,
Het Cox Proportional Gevaren Model
Het Cox Proportional Gevaren Model wordt meestal gegeven in termen van de tijd t, covariate vector x, en de coëfficiënt van de vector β als
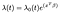
waar de λₒ is een willekeurige functie van de tijd, de baseline hazard. Het puntproduct van X en β wordt genomen in de exponent net als in standaard lineaire regressie., Ongeacht de covariabele waarden delen alle proefpersonen hetzelfde basisrisico λₒ. Daarna worden aanpassingen gemaakt op basis van de covariaten.
interpretatie van de resultaten
stel voor de minuut dat we een Cox Proportional Hazards model hebben aangepast aan onze gegevens, die bestond uit
- Een kolom waarin de tijd voor elke proefpersoon wordt gespecificeerd
- Een kolom waarin wordt gespecificeerd of de proefpersoon “geobserveerd” werd (dat is mislukt, of, in ons voorkeursvoorbeeld, dat zijn ziekte zich heeft ontwikkeld). Een waarde van 1 betekent dat het onderwerp zijn ziekte had vooruitgang., Een waarde van 0 betekent dat de ziekte zich op het laatste observatietijdstip niet had ontwikkeld. De observatie werd gecensureerd.
- kolommen voor onze covariaten X.
Na de pasvorm krijgen we waarden voor β. Stel bijvoorbeeld voor de eenvoud dat er één covariant is. Een waarde van β=0,1 betekent dat een toename van de covariabele met een hoeveelheid van 1 leidt tot een ongeveer 10% hoge kans op ziekteprogressie op een bepaald moment., De exacte waarde is in feite

Voor kleine waarden van β, de waarde van β zelf is een vrij goede benadering van de exacte toename in gevaar. Voor grotere waarden van β moet het exacte bedrag worden berekend.
een andere manier om β=0,1 uit te drukken is dat, naarmate x toeneemt, het gevaar toeneemt met een snelheid van 10% per toename van x met 1. De grotere 10.,52% komt voort uit (continue) compounding, net als bij samengestelde rente.
ook betekent β = 0 geen effect, en β negatief betekent dat er minder risico is naarmate de covariabele toeneemt. Merk op dat, in tegenstelling tot in standaard regressies, er geen intercept term is. In plaats daarvan wordt het intercept geabsorbeerd in het basisrisico λₒ, dat ook kan worden geschat (zie hieronder).
ten slotte, ervan uitgaande dat we de baseline hazard function hebben geschat, kunnen we de survivor function construeren.,
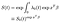
de basislijn functie wordt verhoogd tot de macht van de EXP(xßß) factor afkomstig van de covariaten. Er moet enige voorzichtigheid worden betracht bij het interpreteren van de overlevingsfunctie bij baseline, die ruwweg de rol speelt van de interceptterm in een regelmatige lineaire regressie. Als de covariaten gecentreerd zijn (gemiddelde 0) dan vertegenwoordigt het de overlevingsfunctie voor het “gemiddelde” subject.,
schatting van het Cox Proportional Hazards Model
in de jaren zeventig stelde David Cox, een Britse wiskundige, een manier voor om β te schatten zonder het basisrisico λₒ te moeten schatten. Nogmaals, het baseline gevaar kan achteraf worden geschat. Zoals eerder vermeld, zullen we zien dat het de volgorde van de waargenomen mislukkingen is die telt, niet de tijden zelf.
alvorens in de schatting te springen, is het de moeite waard om de verbanden te bespreken. Aangezien we meestal alleen gegevens in discrete stappen observeren, is het mogelijk dat twee fouten tegelijkertijd kunnen optreden., Bijvoorbeeld, twee machines kunnen falen in dezelfde week, en de opname wordt alleen gemaakt op een wekelijkse basis. Deze banden maken de analyse van de situatie vrij ingewikkeld zonder veel inzicht toe te voegen. Daarom zal ik de schattingen afleiden in het geval van geen banden.
bedenk dat onze gegevens bestaan uit waarnemingen van een aantal fouten op een discreet tijdstip. Laat R (t) wijzen op de populatie “in gevaar” op tijdstip t. als een subject in onze studie heeft gefaald (ziekte verergerd, bijvoorbeeld) voor tijdstip t, zijn ze niet “in gevaar.,”Ook, als een onderwerp in onze studie heeft hun observatie gecensureerd op een moment voor tijd t, ze zijn ook niet “in gevaar.”
op de gebruikelijke manier willen we een waarschijnlijkheidsfunctie construeren (Wat is de waarschijnlijkheid dat we de gegevens die we hebben waargenomen, gezien de covariaten en coëfficiënten) en die vervolgens optimaliseren om een maximale waarschijnlijkheid estimator te krijgen.
voor elke afzonderlijke tijd waarin we een storing van subject j zagen, is de kans dat die optreedt, gegeven het feit dat er een storing is opgetreden, lager. De som wordt overgenomen door alle personen die op tijdstip j een risico lopen.,

merk op dat het basisrisico λₒ is weggevallen! Heel handig. Om deze reden is de waarschijnlijkheid die we construeren slechts een gedeeltelijke waarschijnlijkheid. Merk ook op dat de tijden helemaal niet verschijnen., De term voor subject j hangt alleen af van welke subjecten op tijdstip j nog in leven zijn, wat op zijn beurt alleen afhangt van de volgorde waarin de subjecten worden gecensureerd of zien falen.
De gedeeltelijke waarschijnlijkheid is natuurlijk gewoon het product van deze termen, één voor elke fout die we waarnemen (geen termen voor gecensureerde observaties).,
De log gedeeltelijke kans is dan
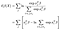
De pasvorm is uitgevoerd met standaard numerieke methoden, bijvoorbeeld in de python package statsmodels en de variantie-covariantie matrix van de ramingen wordt gegeven door de (inverse van de Fisher Informatie Matrix. Niets spannends hier.,
het schatten van de overlevings-functie bij baseline
nu we de coëfficiënten hebben geschat, kunnen we de overlevings-functie schatten. Dit eindigt als zeer vergelijkbaar met het schatten van een Kaplan-Meier curve.
we postuleren termen α geïndexeerd door i. op tijdstip i moet de overlevings-curve bij baseline afnemen met een fractie α die het percentage proefpersonen met een verhoogd risico vertegenwoordigt dat op tijdstip i niet slaagt., In andere woorden
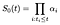
Voor het berekenen van de maximum likelihood schatter voor α, wij achten de kans bijdrage van het onderwerp dat ik dat niet op het moment dat ik en afzonderlijk de bijdrage van degenen die worden gecensureerd op tijdstip i.
Voor een onderwerp dat niet op het moment dat ik de kans wordt gegeven door de kans dat ze in leven zijn, op het moment dat ik minder de kans dat ze leven bij de volgende keer dat ik+1. (We gaan er Tijdelijk van uit dat de tijden zijn geordend).,
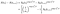
Als ze worden gecensureerd op het moment dat ik de bijdrage is alleen de kans dat ze levend zijn, op het moment nadat ik, dat wil zeggen dat zij nog niet gestorven., Dit is gewoon
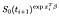
Er is een extra termijn van de onderwerpen die werden waargenomen (d.w.z. waargenomen om te falen in plaats van censored)., De log waarschijnlijkheid wordt
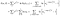
Ik ben een beetje slordig geweest over het bijhouden van eindpunten (i vs.i+1), maar het zal allemaal werken.
Er zijn alleen α-termen voor proefpersonen waarvan we zagen dat ze faalden., Onderscheidend met betrekking tot α-j en uitgaande van geen banden, krijgen we een bijdrage van de som aan de linkerzijde alleen voor personen die op tijdstip j leven, en een enkele bijdrage van de term aan de rechterzijde.,kwa 0 betekent dat we kunnen verkrijgen van de maximum likelihood schattingen voor α met onze schatting voor β als de oplossing voor de verschillende vergelijkingen, één voor elk onderwerp dat werd waargenomen te mislukken:
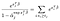
Extensies en Waarschuwingen
Er is veel meer over te zeggen Cox Proportionele Gevaren modellen, maar ik zal proberen om dingen kort en noem een paar dingen.,
men kan bijvoorbeeld rekening houden met tijdsafhankelijke regressoren, en dit is mogelijk.
het andere cruciale ding om in gedachten te houden is weggelaten variabele bias. In standaard lineaire regressie, weggelaten variabelen niet gecorreleerd met de regressoren zijn geen groot probleem. Dit geldt niet voor de overlevingsanalyse. Stel dat we twee even grote en bemonsterde subpopulaties in onze gegevens hebben, elk met een constant hazard rate, één is 0,1 en de andere is 0,5. In eerste instantie zullen we een hoog hazard rate zien (het gemiddelde, slechts 0,3)., Naarmate de tijd vordert, zal de populatie met een hoog risicopercentage de populatie verlaten en zullen we een risicopercentage waarnemen dat daalt naar 0,1. Als we de variabele die deze twee populaties vertegenwoordigt weglaten, zal onze basislijn gevarenratio helemaal in de war zijn.