
Pythagoras
meer dan 2000 jaar geleden was er een verbazingwekkende ontdekking over driehoeken:
wanneer een driehoek een rechte hoek heeft (90°) …
… en vierkanten zijn gemaakt op elk van de drie zijden,…
… dan heeft het grootste vierkant precies dezelfde oppervlakte als de andere twee vierkanten bij elkaar!,
Het heet “Pythagoras” Theorema” en kan geschreven worden in een korte vergelijking:
a2 + b2 = c2
Opmerking:
- c is de langste zijde van de driehoek
- a en b zijn de twee andere zijden
Definitie
De langste zijde van de driehoek wordt genoemd de “schuine zijde”, zodat de formele definitie is:
In een rechthoekige driehoek:het kwadraat van de schuine zijde gelijk is aan
de som van de kwadraten van de twee andere zijden.,
zeker … ?
laten we eens kijken of het echt werkt met een voorbeeld.

Waarom is dit nuttig?
als we de lengte van twee zijden van een rechthoekige driehoek kennen, kunnen we de lengte van de derde zijde vinden. (Maar vergeet niet het werkt alleen op rechthoekige driehoeken!)
Hoe gebruik ik het?,
Schrijf het als een vergelijking:
 |
a2 + b2 = c2 |
Dan we gebruik van algebra te vinden van de ontbrekende waarde, zoals in deze voorbeelden:
U kunt ook lezen over Kwadraten en vierkantswortels uit te vinden waarom √169 = 13
Het werkt het andersom ook: als de drie zijden van een driehoek maken a2 + b2 = c2, dan is de driehoek een rechthoekige.,
en u kunt de stelling zelf bewijzen !
pak papier pen en schaar, gebruik dan de volgende animatie als leidraad:
- teken een rechthoekige driehoek op het papier, waardoor er veel ruimte overblijft.,
- Tekenen van een vierkant langs de schuine zijde (de langste zijde)
- Tekenen van dezelfde grootte plein aan de andere kant van de schuine zijde
- Tekenen van lijnen zoals aangegeven op de animatie, zoals deze:

- Knip de vormen
- zorgen dat u kunt aantonen dat het grote vierkant heeft dezelfde oppervlakte als de twee pleinen aan de andere zijden
Andere, heel Eenvoudig, Het bewijs
Hier is een van de oudste bewijzen dat het vierkant op de lange zijde is hetzelfde gebied als de andere pleinen.,
bekijk de animatie en let op wanneer de driehoeken beginnen te schuiven.
u kunt de animatie een paar keer bekijken om te begrijpen wat er gebeurt.
De paarse driehoek is de belangrijkste.
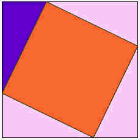 |
wordt | 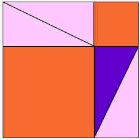 |

