“Ik ben er in ieder geval van overtuigd dat het gooit geen dobbelstenen.,”
~ Albert Einstein
- Random Variabelen
- Discrete Random Variabelen
- Continue Random Variabelen
- Gemengde Random Variabelen
- Cumulatieve verdelingsfuncties (CDF)
- kansdichtheidsfunctie (PDF)
- Interactieve CDF/PDF-Voorbeeld
Random Variabelen:

Zeggen dat je met een munt uit je zak en gooi het in de lucht. Terwijl het door de ruimte draait, wat zou je kunnen zeggen over zijn toekomst?
zal het land heads up? Munt?, Meer dan dat, hoe lang blijft het in de lucht? Hoe vaak zal het stuiteren? Hoe ver van waar het de grond raakt zal het uiteindelijk tot rust komen? Wat dat betreft, zal het ooit de grond raken? Ooit tot rust gekomen?
voor sommige van dergelijke vragen kunnen we al lang voor observaties antwoorden vinden en doen we dat ook; we zijn er vrij zeker van dat de zwaartekracht het zal houden en dat de munt zal landen. Maar voor anderen hebben we geen andere keuze dan te oordelen en in meer vage termen te spreken, als we iets nuttigs over de toekomst willen zeggen.,
als wetenschappers is het natuurlijk onze taak om iets nuttigs (of op zijn minst gezaghebbend) te zeggen…), terwijl de metaforische munten van belangrijke fysieke systeem zijn nog steeds in de lucht. Kop of munt kan zelfs een kwestie van leven of dood zijn. Onze munten kunnen bijvoorbeeld verschillende mogelijke koelvloeistofdebieten of massa ‘ s uranium in een kerncentrale zijn. We willen graag weten wat onze kansen zijn dat we draaiende turbines krijgen in plaats van een kernsmelting.,
voor een strikte determinist werden al dergelijke weddenschappen afgewikkeld lang voordat een munt, metaforisch of niet, ooit geslagen werd; we weten het gewoon nog niet. Als we alleen maar wisten de krachten toegepast op een munt ‘ s toss, De exacte verdeling van de massa, de verschillende minuten bewegingen van de lucht in de kamer… Als we dat allemaal wisten, dan zouden we weten dat bepaalde toss een 100% kans had om te landen zoals het zal landen, en geen kans op een andere uitkomst.
maar we missen natuurlijk vaak zelfs een noemenswaardige fractie van dergelijke kennis van de wereld., Bovendien lijkt het op zeer kleine schaal dat strikte deterministen absoluut ongelijk hebben; er is geen manier om te voorspellen wanneer, bijvoorbeeld, een uraniumatoom zal splitsen, en als een dergelijke gebeurtenis de grotere wereld beïnvloedt, dan is die macro-gebeurtenis echt onvoorspelbaar. Sommige resultaten zijn echt in de lucht, onrustig totdat ze deel uitmaken van het verleden.
om met deze realiteit om te gaan en om de toekomstige toestanden van een systeem op een nuttige manier te kunnen beschrijven, gebruiken we willekeurige variabelen., Een willekeurige variabele is gewoon een functie die elke mogelijke fysieke uitkomst van een systeem relateert aan een uniek, reëel getal. Als zodanig zijn er drie soorten willekeurige variabelen: discreet, continu en gemengd. In de volgende paragrafen zullen deze categorieën kort worden besproken en zullen voorbeelden worden gegeven.
Discrete willekeurige variabelen:
overweeg onze toss opnieuw. We kunnen kop of munt hebben als mogelijke uitkomst. Als we een variabele, x, definiëren als het aantal koppen in een enkele worp, dan kan x mogelijk 1 of 0 zijn, niets anders., Een dergelijke functie, x, zou een voorbeeld zijn van een discrete willekeurige variabele. Dergelijke willekeurige variabelen kunnen alleen discrete waarden aannemen. Andere voorbeelden zijn de mogelijke resultaten van een zwangerschapstest, of het aantal studenten in een klaslokaal.
continue willekeurige variabelen:
terug naar de toss, wat als we de afstand wilden beschrijven tussen waar onze munt tot rust kwam en waar hij voor het eerst de grond raakte. Die afstand, x, zou een continue willekeurige variabele zijn omdat het een oneindig aantal waarden zou kunnen aannemen binnen het continue bereik van reële getallen., De munt kan reizen 1 cm, of 1,1 cm, of 1.11 cm, of op en op. Andere voorbeelden van continue willekeurige variabelen zijn de massa van sterren in ons melkwegstelsel, de pH van oceaanwater, of de verblijftijd van een analyt in een gaschromatograaf.
gemengde willekeurige variabelen:
gemengde willekeurige variabelen hebben zowel discrete als continue componenten. Dergelijke willekeurige variabelen worden zelden aangetroffen. Voor een mogelijk voorbeeld, hoewel, kunt u het meten van het gewicht van een monster en beslissen dat elk gewicht gemeten als een negatieve waarde zal worden gegeven een waarde van 0., Op die manier heeft de willekeurige variabele een discrete component op x = 0 en een continue component waar x > 0.
cumulatieve distributiefuncties (CDF):
de vraag rijst natuurlijk hoe willekeurige variabelen het best wiskundig te beschrijven (en visueel weer te geven). Voor deze taken maken we gebruik van waarschijnlijkheidsdichtheidsfuncties (PDF) en cumulatieve dichtheidsfuncties (CDF). Aangezien CDFs eenvoudiger te begrijpen zijn voor zowel discrete als continue willekeurige variabelen dan PDF ‘ s, zullen we eerst CDFs uitleggen.
overweeg het gooien van een eerlijke 6-sidded dobbelsteen., We zouden een 1 op 6 kans hebben om een van de mogelijke waarden van de willekeurige variabele te krijgen (1, 2, 3, 4, 5, 6). Als we deze mogelijke waarden op de x-as plotten en de waarschijnlijkheid van het meten van elke specifieke waarde, x, of een waarde kleiner dan x op de y-as plotten, zullen we de CDF van de willekeurige variabele hebben.
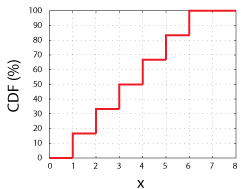
CDF voor een eerlijke 6-Sidded dobbelsteen. Merk op dat elke stap is een hoogte van 16,67%, of 1 op 6.
Deze functie, CDF (x), vertelt ons eenvoudig de kansen van het meten van een waarde tot en met x., Als zodanig moeten alle CDF ‘ s deze kenmerken hebben:
- een CDF moet gelijk zijn aan 0 wanneer x = -∞, en benadering 1 (of 100%) als x nadert +∞. Simpel gezegd, van alle mogelijke uitkomsten moet er een uitkomst zijn; de kans op het gooien van een zeszijdige dobbelsteen en het krijgen van een waarde tussen -∞ en ∞ is 100%.
- de helling van een CDF moet altijd gelijk zijn aan of groter zijn dan nul. Denk bijvoorbeeld aan de kans op het gooien van een 6-sidded dobbelsteen (eerlijk of niet) en het verkrijgen van een waarde tussen 0 en 4., Die kans kan onmogelijk meer zijn dan de kans op het verkrijgen van een waarde tussen 0 en 5, omdat de kansen van een 1, 2, of 3 landing gezicht omhoog zijn, natuurlijk, altijd een fractie van de kansen op het krijgen van een 1, 2, 3, of 4.
voor een voorbeeld van een continue willekeurige variabele toont het volgende applet de normaal gedistribueerde CDF.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Merk gewoon op dat de kenmerken van een CDF hierboven beschreven en uitgelegd voor een discrete willekeurige variabele hold voor continue willekeurige variabelen ook.
voor meer intuïtieve voorbeelden van de eigenschappen van CDFs, zie het interactieve voorbeeld hieronder. Ook interactieve percelen van vele andere CDF ‘ s belangrijk voor het gebied van de statistiek en gebruikt op deze site kan hier worden gevonden.
Kansdichtheidsfuncties (PDF):
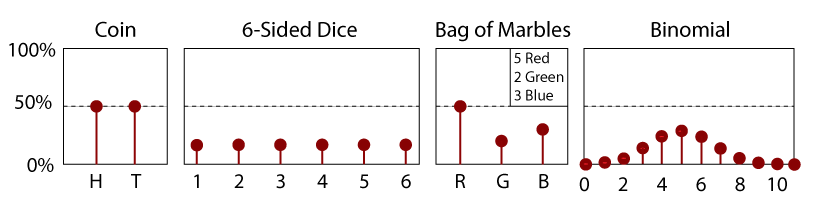
PDF voor een eerlijke 6-Sidded dobbelsteen.
een PDF is gewoon de afgeleide van een CDF., Een PDF is dus ook een functie van een willekeurige variabele, x, en zijn grootte zal een indicatie zijn van de relatieve waarschijnlijkheid van het meten van een bepaalde waarde. Omdat het de helling van een CDF is, moet een PDF altijd positief zijn; er zijn geen negatieve kansen voor een gebeurtenis. Bovendien is per definitie het oppervlak onder de kromme van een PDF(x) tussen -∞ en x gelijk aan zijn CDF(x). Als zodanig geeft het gebied tussen twee waarden x1 en x2 de kans om een waarde binnen dat bereik te meten.
de volgende applet toont een voorbeeld van de PDF voor een normaal gedistribueerde willekeurige variabele, x.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., overweeg ook het verschil tussen een continue en discrete PDF. Hoewel een discrete PDF (zoals hierboven getoond voor dice) je de kans geeft om een bepaald resultaat te behalen, zijn waarschijnlijkheden met continue PDF ‘ s Zaken van bereik, niet van discrete punten. Bijvoorbeeld, er is duidelijk een 1 op 6 (16,6%) kans op het gooien van een 3 op een dobbelsteen, zoals te zien is in de PDF. Maar wat is het vreemde van het meten van precies nul met een willekeurige variabele met een normale PDF en gemiddelde van nul, zoals hierboven getoond? Ook al is het de waarde waar de PDF het grootst is, de kans om precies 0,00000 te meten..,. is, misschien contra-intuïtief, nul. De kans dat een willekeurig getal oneindig nauwkeurig wordt gemeten, is in feite nul. met een continue PDF kunt u in plaats daarvan vragen wat de kans is dat u tussen twee waarden zult meten om een waarschijnlijkheid te verkrijgen die groter is dan nul. Om deze kans te vinden gebruiken we gewoon de CDF van onze willekeurige variabele., Omdat de CDF ons het oneven vertelt van het meten van een waarde of iets lager dan die waarde, om de waarschijnlijkheid te vinden van het meten tussen twee waarden, x1 en x2 (waarbij x1 > x2), moeten we gewoon de waarde van de CDF op x1 nemen en daarvan de waarde van de CDF op x2 Aftrekken. Bijvoorbeeld, met behulp van de normale CDF in de applet hierboven (Met μ = 0, en σ = 1), als we wilden weten de kansen van het meten tussen 0,01 en 0,02 vinden we CDF(x=0,1)=53,9828% en CDF(x=0,2)=57,9260%. Dan geeft het verschil, CDF(0.2)-CDF(0.1), ons de kansen van ongeveer 3.9% van het meten van een x tussen 0,1 en 0,2., voor meer intuïtieve, visuele voorbeelden van de eigenschappen van PDF ‘ s, zie het interactieve voorbeeld hieronder. Ook interactieve percelen van vele belangrijke PDF ‘ s die op deze site worden gebruikt, zijn hier te zien. |
|||||||||||||||||