Conteúdo – funções de densidade de Probabilidade

Conteúdo

funções de densidade de Probabilidade

A função de densidade de probabilidade (pdf) \(f(x)\) de uma variável aleatória contínua \(X\) é definido como a derivada da cdf \(F(x)\):

\

por Isso, às vezes, é útil considerar o cdf \(F(x)\) em termos de pdf \(f(x)\):

\

O pdf \(f(x)\) tem duas propriedades importantes:

1. \(f(x) \geq 0\), para todo o \(x\)
2. \(\displaystyle\int_{-\infty}^{\infty} f(x)\;dx = 1\).,

uma variedade infinita de formas são possíveis para um pdf, uma vez que os únicos requisitos são as duas propriedades acima. O pdf pode ter um ou vários picos, ou nenhum pico em tudo; pode ter descontinuidades, ser feita de combinações de funções, e assim por diante. a figura 5 mostra um pdf com um único pico e alguma habilidade suave. Como é o caso de um pdf típico, o valor da função aproxima-se de zero como \(x \a \infty\) e \(x \a – \infty\).

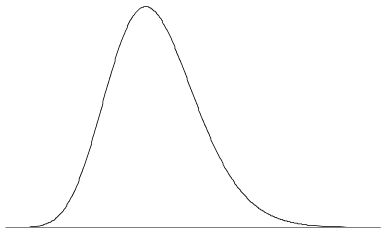
Figure 5: a pdf may look something like this.,

agora exploramos como as probabilidades relativas à variável aleatória contínua \(X\) se relacionam com o seu pdf. O resultado importante aqui é que

\_a^B.\]

Este resultado decorre do facto de ambos os lados serem iguais a \(F (b) – F(a)\).

notas.

• para uma variável aleatória contínua, devemos considerar a probabilidade de que ela se encontra em um intervalo. A importância deste resultado é que ele nos diz que, para encontrar a probabilidade, precisamos encontrar a área sob o pdf no intervalo dado.
• a área total sob o pdf é igual a 1., Então este resultado nos diz que, para aproximar a probabilidade de que a variável aleatória esteja em um dado intervalo, nós apenas temos que adivinhar a fração da área sob o pdf entre as extremidades do intervalo.
• este resultado fornece outra perspectiva sobre por que pdfs não pode ser negativo, uma vez que se fossem, uma probabilidade negativa poderia ser obtida, o que é impossível.
• o pdf é análogo, mas diferente de, a função de probabilidade (pf) para uma variável aleatória discreta. Um pf dá uma probabilidade, então não pode ser maior que um., Um pdf \(f (x)\), no entanto, pode dar um valor maior do que um para alguns valores de \(x\), uma vez que não é o valor de \(f(x)\), mas a área sob a curva que representa a probabilidade. Por outro lado, a altura da curva reflete a probabilidade relativa. Se \(f (b) = 2f (a)\), então uma observação próxima a \(b\) é aproximadamente duas vezes mais provável que uma observação próxima a \(a\).,

Próxima página – Conteúdo – Média e variância de uma variável aleatória contínua