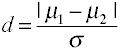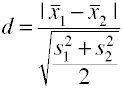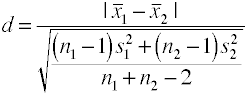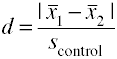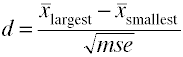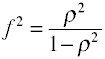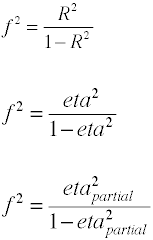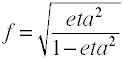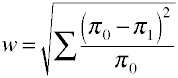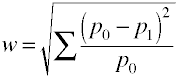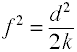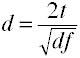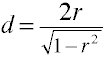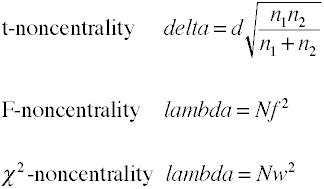uma utilização do tamanho do efeito é como um índice padronizado que é independente do tamanho da amostra e quantifica a magnitude da diferença entre as populações ou a relação entre as variáveis explicativas e de resposta. Outro uso do tamanho do efeito é o seu uso na análise do poder de execução.
tamanho do Efeito para a diferença no meio
tamanho do Efeito para as diferenças no meio é dada byCohen d é definido em termos de população significa (µs) e de uma população standarddeviation (σ), como mostrado abaixo.,
Usando o root mean square desvio padrão
Usando o pool de desvio-padrão (Hedge ” g)
Esta versão de Cohen d usa o pool de desvio padrão e também é conhecido como “Hedge” g.,
Você pode facilmente obter este valor a partir de uma anova programa tomando a raiz quadrada da meansquare de erro que também é conhecido como o erro médio quadrático.
Using the control group standard deviation (Glass’ Δ)
Another version of Cohen’s d using the standard deviation for the control group is also known asglass’ Δ.,
, em seguida, Mais dois grupos
Quando existem mais de dois grupos de utilizar a diferença entre o maior e smallestmeans dividido pela raiz quadrada da média do quadrado do erro.
Effect size for F-ratios in regression analysis
para a regressão OLS, a medida do tamanho dos efeitos é F, Que é definida por Cohen da seguinte forma.,
mais uma Vez há várias maneiras em que o tamanho do efeito pode ser calculada a partir de dados de exemplo. Notethat η2 é outro nome para R2.
tamanho do Efeito para a F-rácios de análise de variância
O tamanho do efeito utilizado na análise de variância é definida pela razão entre a população standarddeviations.,
tamanho do Efeito do χ2, a partir de tabelas de contingência
mais uma Vez vamos começar com a definição de fórmula em termos de valores da população.O tamanho do efeito w é a raiz quadrada da estatística padrão do Qui-quadrado.,
E aqui é como w é calculado usando dados de exemplo.
Aqui está uma tabela de valores sugeridos para baixo, médio e alto efeitos (Cohen, 1988). Estes valores não devem ser considerados absolutos e devem ser interpretados no contexto do seu programa de investigação. Os valores para efeitos grandes são frequentemente excedidos na prática, com valores de D de Cohen superiores a 1, 0 não incomuns.,No entanto, o uso de tamanhos de efeito muito grandes em análise de potência prospectiva não é provavelmente uma boa idéia, pois poderia levar a estudos sob energia.,fórmulas
, onde k = número de grupos
Converter t a d por dois grupos independentes
Converter em r a d por dois grupos independentes
Noncentrality estimativas
Poder de análise através de métodos analíticos requerem uma estimativa de noncentrality que é basicallythe tamanho de efeito multiplicado por uma amostra de tamanho fator., Aqui estão algumas fórmulas para estimar a não centralidade.
Exemplo de análise do poder
Aqui está um exemplo que reúne tamanho do efeito e noncentrality em uma análise do poder.
considere uma análise de Sentido Único da variância com três grupos (k = 3). Se esperarmos que o andeta2 seja igual .,12, caso em que o efeito será o tamanho
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
Com uma projeção do tamanho da amostra de 60 a estimativa de noncentrality é
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
O número de graus de liberdade k-1 = 3-1 = 2, enquanto que o denominador gl é N-k = 60-3 = 57.O valor crítico de F com 2 e 57 graus de liberdade é 3.16. O que resulta em um poder de
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
assim, um N de 60 e tamanho de efeito de .369 yields a projected power of about .7.
podemos melhorar a potência de .7 utilizando uma amostra projectada de 75 em vez de 60., Com o mesmo efeito Tamanho de.369, we get a new noncentrality estimate of
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
The numerator degrees of freedom remain the same while the denominator df now equal N-k = 75-3 = 72.O valor crítico de F com 2 e 72 graus de liberdade de 3.12. Desta vez a potência é
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
que está dentro de limites de pesquisa aceitáveis.
Por Favor, note que diferentes pacotes de estatísticas usam nomes diferentes e uma ordem diferente de argumentos na função a que chamamos noncentralFtail. Terá de ler a documentação que acompanha o seu software.,
Becker, L. Psychology 590 course notes. Viewed 19 Jun 2009 < http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen, J. 1988. Análise estatística de poder para as ciências comportamentais. Hillsdale, New Jersey: Lawrence Erlbaum Associates