O coeficiente α é o mais amplamente utilizado procedimento para a estimativa da confiabilidade na pesquisa aplicada. Como afirmado por Sijtsma (2009), sua popularidade é tal que Cronbach (1951) tem sido citado como uma referência mais frequentemente do que o artigo sobre a descoberta da dupla hélice do DNA., No entanto, suas limitações são bem conhecidas (Lord e Novick, 1968; Cortina, 1993; Yang e Green, 2011), algumas das mais importantes são as suposições de erros não correlacionados, Tau-equivalência e normalidade.
O pressuposto de não correlacionada erros (erro de pontuação de qualquer par de itens é não correlacionada) é uma hipótese da Teoria Clássica (Lord e Novick, 1968), violação de o que poderá implicar a presença de complexas estruturas multidimensionais que requerem procedimentos de estimação que tomar essa complexidade em conta (por exemplo, Tarkkonen e Vehkalahti, 2005; Green e Yang, 2015)., É importante arrancar a crença errônea de que o coeficiente α é um bom indicador de unidimensionalidade porque seu valor seria maior se a escala fosse unidimensional. Na verdade, o oposto é exatamente o caso, como foi mostrado por Sijtsma (2009), e sua aplicação em tais condições pode levar a confiabilidade ser fortemente sobrestimado (Raykov, 2001). Por conseguinte, antes de calcular α, É necessário verificar se os dados se encaixam em modelos unidimensionais.= = ver também = = * Tau-equivalência = = ligações externas = = ,, a mesma pontuação verdadeira para todos os itens de teste, ou igual carga de fator de todos os itens em um modelo fatorial) é um requisito para α ser equivalente ao coeficiente de confiabilidade (Cronbach, 1951). Se a suposição de tau-equivalência é violada a verdadeira confiabilidade valor vai ser subestimada (Raykov, 1997; Graham, 2006) por uma quantia que pode variar entre 0,6 e 11,1%, dependendo da gravidade da violação (Verde e Yang, 2009a). Trabalhar com dados que obedeçam a esta suposição não é geralmente viável na prática (Teo e Fan, 2013); o modelo congenérico (i.e.,, diferentes cargas de fator) é o mais realista.
O requisito de normalidade multivariante é menos conhecido e afecta tanto a estimativa da fiabilidade puntual como a possibilidade de estabelecer intervalos de confiança (Dunn et al., 2014). Sheng e Sheng (2012) observaram recentemente que quando as distribuições são distorcidas e/ou leptokurtic, uma polarização negativa é produzida quando o coeficiente α é calculado; resultados semelhantes foram apresentados por Verde e Yang (2009b), em uma análise dos efeitos da não-normalidade das distribuições na estimativa da confiabilidade., O estudo dos problemas de skewness é mais importante quando vemos que, na prática, os pesquisadores habitualmente trabalham com escamas skewed (Micceri, 1989; Norton et al., 2013; Ho e Yu, 2014). Por exemplo, Micceri (1989) estimou que cerca de 2/3 da capacidade e mais de 4/5 das medidas psicométricas exibiam pelo menos uma assimetria moderada (i.e. Apesar disso, o impacto da destreza na estimativa da fiabilidade foi pouco estudado.,
Considerando a abundante literatura sobre as limitações e os preconceitos do coeficiente α (Revelle e Zinbarg, 2009; Sijtsma, 2009, 2012; Cho e Kim, De 2015; Sijtsma e van der Arca, 2015), a pergunta que surge é: por que os pesquisadores continuam a usar α alternativas coeficientes de existir que superar essas limitações. É possível que o excesso de procedimentos para estimar a confiabilidade desenvolvido no século passado tenha oscurado o debate. Isto teria sido ainda agravado pela simplicidade de cálculo deste coeficiente e pela sua disponibilidade em softwares comerciais.,
A dificuldade de estimar o coeficiente de fiabilidade do pxx reside na sua definição PXX’=σt2∕σx2, que inclui a pontuação verdadeira no numerador de variância quando esta é, por natureza, não observável. O coeficiente α tenta aproximar esta variância não observável da covariância entre os itens ou componentes. Cronbach (1951) mostrou que, na ausência de equivalência tau, o coeficiente α (ou lambda 3 de Guttman, que é equivalente a α) era uma boa aproximação do limite inferior., Assim, quando as premissas são violados o problema traduz-se em encontrar a melhor limite inferior; na verdade, este nome é dado ao Maior limite Inferior do método (GLB) qual é a melhor possível aproximação de um ângulo teórico (Jackson e Agunwamba, 1977; Woodhouse, e Jackson, 1977; Shapiro e dez Berge, 2000; Sočan, 2000; ten Berge e Sočan, 2004; Sijtsma, 2009). No entanto, Revelle e Zinbarg (2009) consideram que ω dá um limite mais baixo do que o GLB., Há, portanto, um debate por resolver sobre qual destes dois métodos dá o melhor limite inferior; além disso, a questão da não-normalidade não foi exaustivamente investigada, como discute o presente trabalho.
ω Coeficientes
McDonald (1999) propôs o wt coeficiente para a estimativa de confiabilidade a partir de uma análise fatorial framework, que pode ser expresso formalmente como:
Onde λj é o carregamento do item j, λj2 é uma comunhão de item j e ψ equivale a singularidade., O coeficiente de wt, ao incluir as lambdas em suas fórmulas, é adequado tanto quando Tau-equivalência (isto é, cargas de fator iguais de todos os itens de teste) existe (WT coincide matematicamente com α), e quando itens com diferentes discriminações estão presentes na representação da construção (isto é, diferentes cargas de fator dos itens: medidas congenéricas). Consequentemente, a wt corrige o viés de subestimação de α quando a suposição de Tau-equivalência é violada (Dunn et al., 2014) e diferentes estudos mostram que é uma das melhores alternativas para estimar a confiabilidade (Zinbarg et al.,, 2005, 2006; Revelle e Zinbarg, 2009).
Quando existe correlação entre os erros, ou há mais do que uma dimensão latente nos dados, a contribuição de cada dimensão para a variância total explicada é estimada, obtendo-se o chamado hierárquica ω (wh), que nos permite corrigir o pior superestimação viés de α com dados multidimensionais (ver Tarkkonen e Vehkalahti, 2005; Zinbarg et al., 2005; Revelle and Zinbarg, 2009)., Coeficientes W e WT são equivalentes em dados unidimensionais, então vamos nos referir a este coeficiente simplesmente como ω.
a Maior limite Inferior (GLB)
Sijtsma (2009) mostra em uma série de estudos que um dos mais poderosos estimadores de confiabilidade é GLB—deduzido pelo Woodhouse e Jackson (1977), a partir de pressupostos da Teoria Clássica (Cx = Ct + Ce)—inter-item da matriz de covariância observada item pontuação Cx. Divide-se em duas partes: a soma da matriz de covariância entre itens para as pontuações verdadeiras do item Ct; e a matriz de covariância de erro entre itens Ce (ten Berge e Sočan, 2004)., Sua expressão é:
em que σx2 é a variância de teste e tr (Ce) refere-se ao traço da matriz de covariância de erro entre itens que se revelou tão difícil de estimar. Uma solução tem sido a utilização de procedimentos fatoriais, tais como análise de Fator de classificação mínima (um procedimento conhecido como glb.fa). Mais recentemente, o procedimento algébrico GLB (GLBa) foi desenvolvido a partir de um algoritmo concebido por Andreas Moltner (Moltner e Revelle, 2015)., De acordo com Revelle (2015a) este procedimento adota a forma que é mais fiel ao original de definição de Jackson e Agunwamba (1977), e tem a vantagem de introduzir um vetor de peso dos itens por importância (Al-Homidan, 2008).apesar dos seus pontos fortes teóricos, o GLB tem sido muito pouco utilizado, embora alguns estudos empíricos recentes tenham demonstrado que este coeficiente produz melhores resultados do que o α (Lila et al., 2014) e α e ω (Wilcox et al., 2014)., No entanto, em pequenas amostras, sob o pressuposto de normalidade, tende a sobrestimar o verdadeiro valor de confiabilidade (Shapiro e ten Berge, 2000); no entanto, o seu funcionamento em condições não normais permanece desconhecido, especificamente quando as distribuições dos itens são assimétricas.
Considerando os coeficientes definidos acima, e os preconceitos e limitações de cada um, o objeto deste trabalho é avaliar a robustez destes coeficientes, na presença de assimétrico itens, considerando, também, a suposição de tau-a equivalência e o tamanho da amostra.,
Métodos
de Geração de Dados
Os dados foram gerados usando o R (R Development Core Team, 2013) e RStudio (Racine, 2012) de software, seguindo o modelo fatorial:
onde Xij é a resposta simulada de assunto eu no item j, λjk é o carregamento do item j no Fator k (que foi gerado pelo modelo unifactorial); Fk é o fator latente gerado por um padrão de distribuição normal (média 0 e variância 1), e ej é a aleatória do erro de medição de cada item também seguir um padrão de distribuição normal.,
Distorcida itens: Padrão normal Xij foram transformados para gerar a não-normalidade das distribuições utilizando o procedimento proposto por Headrick (2002) a aplicação de quinta ordem polinomial transforma:
Condições Simuladas
Para avaliar o desempenho dos coeficientes de confiabilidade (α, ω, GLB e GLBa) nós trabalhamos com três tamanhos de amostra (250, 500, 1000), dois tamanhos: curto (6 itens) e longo (12 itens), duas condições de tau-equivalência (uma com tau-equivalência e um sem, i.é.,, congeneric) e a incorporação progressiva de itens assimétricos (de todos os itens sendo normal para todos os itens sendo assimétrico). No curto testar a confiabilidade foi fixado em 0.731, que na presença de tau-equivalência é atingido com seis itens com fator de cargas = 0.558; enquanto o congeneric modelo é obtido através da definição de fator de cargas em valores de 0.3, 0.4, 0.5, 0.6, 0.7, e 0,8 (ver Anexo I). No longo Teste de 12 itens a confiabilidade foi fixada em 0.,845 tomando os mesmos valores que no teste curto tanto para a Tau-equivalência quanto para o modelo congenérico (neste caso, havia dois itens para cada valor de lambda). Desta forma, foram simuladas 120 condições com 1000 réplicas em cada caso.
Análise de Dados
As principais análises foram realizadas utilizando o Psych (Revelle, 2015b) e GPArotation (Bernaards e Jennrich, 2015) pacotes, que permitem α e ω a ser estimado. Foram utilizadas duas abordagens computadorizadas para estimar o GLB: o glb.fa (Revelle, 2015a) e glb.,algebraic (Moltner and Revelle, 2015), este último trabalho de autores como Hunt e Bentler (2015).
A fim de avaliar a exatidão dos vários estimadores na recuperação da confiabilidade, calculamos o quadrado médio de erro raiz (RMSE) e o viés. A primeira é a média das diferenças entre a fiabilidade estimada e a simulada e é formalizada como:
Em Que ρ^ é a fiabilidade estimada para cada coeficiente, ρ a fiabilidade simulada e Nr o número de réplicas., O % viés é entendida como a diferença entre a média estimada de confiabilidade e simulação de confiabilidade e é definido como:
Em ambos os índices, quanto maior o valor, maior será a imprecisão do estimador, mas, ao contrário de RMSE, o viés pode ser positivo ou negativo; neste caso, informações adicionais poderão ser obtidas se o coeficiente de subestimar ou sobrestimar o simulado confiabilidade parâmetro., Seguindo a recomendação de Hoogland e Boomsma (1998) os valores de RMSE < 0,05 e % de viés < 5% foram considerados aceitáveis.
resultados
Os principais resultados podem ser vistos na Tabela 1 (6 itens) e na Tabela 2 (12 itens). Estes mostram a tendência RMSE e % dos coeficientes em Tau-equivalência e Condições congenéricas, e como a habilidade da distribuição de teste aumenta com a incorporação gradual de itens assimétricos.
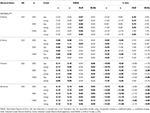
a Tabela 1., RMSE and Bias with tau-equivalence and congeneric condition for 6 items, three sample sizes and the number of skewed items.
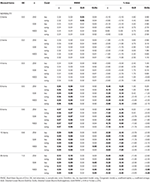
Tabela 2. RMSE and Bias with tau-equivalence and congeneric condition for 12 items, three sample sizes and the number of skewed items.
apenas em condições de Tau-equivalência e normalidade (skewness < 0,2) é observado que o coeficiente α estima a fiabilidade simulada corretamente, Como ω., Na condição congenérica ω corrige a subestimação de α. Tanto o GLB quanto o GLBa apresentam um viés positivo sob normalidade, no entanto o GLBa mostra aproximadamente ½ menor viés do que o GLB (Ver Tabela 1). Se considerarmos o tamanho da amostra, observamos que à medida que o tamanho do teste aumenta, o viés positivo do GLB e do GLBa diminui, mas nunca desaparece.
em condições assimétricas, vemos na Tabela 1 que tanto α Como ω apresentam um desempenho inaceitável com aumento da RM e subavaliações que podem chegar a viés > 13% para o coeficiente α (entre 1 e 2% mais baixo para ω)., Os coeficientes GLB e GLBa apresentam um valor RMSE inferior quando aumenta a inclinação do ensaio ou o número de itens assimétricos (ver quadros 1, 2). O coeficiente de GLB apresenta melhores estimativas quando o valor de distorção do ensaio é de cerca de 0,30; GLBa é muito semelhante, apresentando melhores estimativas do que ω Com um valor de distorção do ensaio de cerca de 0,20 ou 0,30. No entanto, quando o valor skewness aumenta para 0,50 ou 0,60, o GLB apresenta melhor desempenho do que o GLBa. O tamanho do teste (6 ou 12 items) tem um efeito muito mais importante do que o tamanho da amostra na precisão das estimativas.,
Discussão
neste estudo, quatro fatores foram manipuladas: tau-equivalência ou congeneric modelo, o tamanho da amostra (250, 500 e 1000), o número de itens de teste (6 e 12) e o número de assimétrico itens (a partir de 0 assimétrico itens para todos os itens que estão sendo assimétrico), a fim de avaliar a robustez para a presença de assimétrico de dados em quatro confiabilidade coeficientes analisados. Estes resultados são discutidos abaixo.,
em condições de equivalência tau, os coeficientes α e ω convergem, no entanto, na ausência de equivalência tau (congenérica), ω sempre apresenta melhores estimativas e menor tendência RMSE e % viés do que α. Neste mais realista condição, portanto, (Verde e Yang, 2009a; Yang e Verde, 2011), α torna-se um negativamente tendenciosa confiabilidade do estimador (Graham, 2006; Sijtsma, 2009; Cho e Kim, 2015) e ω é sempre preferível ao α (Dunn et al., 2014). No caso de não violação do pressuposto de normalidade, ω é o melhor estimador de todos os coeficientes avaliados (Revelle e Zinbarg, 2009).,
voltando-se para o tamanho da amostra, observamos que este fator tem um pequeno efeito sob normalidade ou um ligeiro afastamento da normalidade: a RMSE e o viés diminuem à medida que o tamanho da amostra aumenta. No entanto, pode-se dizer que para estes dois coeficientes, com tamanho de amostra de 250 e normalidade obtemos estimativas relativamente precisas (Tang e Cui, 2012; Javali et al., 2011)., Para o GLB e GLBa coeficientes, como o tamanho da amostra aumenta o RMSE e o preconceito tende a diminuir; no entanto, eles mantêm um viés positivo para a condição de normalidade, mesmo com grandes tamanhos de amostra de 1000 (Shapiro e dez Berge, 2000; ten Berge e Sočan, 2004; Sijtsma, 2009).
para o tamanho do teste geralmente observamos uma maior RMSE e viés com 6 itens do que com 12, sugerindo que quanto maior o número de itens, menor a RMSE e o viés dos estimadores (Cortina, 1993). Em geral, a tendência é mantida para 6 e 12 itens.,
Quando olhamos para o efeito de, progressivamente, incorporando assimétrico itens para o conjunto de dados, podemos observar que o coeficiente α é altamente sensível à assimétrico itens; estes resultados são semelhantes aos encontrados por Sheng e Sheng (2012) e Verde e Yang (2009b). Coeficiente ω apresenta valores RMSE e viés semelhantes aos de α, mas ligeiramente melhores, mesmo com Tau-equivalência. Verificou-se que o GLB e o GLBa apresentam melhores estimativas quando o desvio do ensaio se afasta de valores próximos de 0.
Considerando que na prática é comum encontrar dados assimétricos (Micceri, 1989; Norton et al.,, 2013; Ho e Yu, 2014), a sugestão de Sijtsma (2009) de usar o GLB como estimador de confiabilidade parece bem fundada. Outros autores, como Revelle e Zinbarg (2009) e Green e Yang (2009a), recomendam o uso de ω, No entanto este coeficiente só produziu bons resultados na condição de normalidade, ou com baixa proporção de itens skewness. Em qualquer caso, estes coeficientes apresentaram maiores vantagens teóricas e empíricas do que α. No entanto, recomendamos aos pesquisadores que estudem não apenas estimativas pontuais, mas também que façam uso da estimativa do intervalo (Dunn et al., 2014).,
estes resultados estão limitados às condições simuladas e presume-se que não há correlação entre erros. Isso seria necessário realizar mais pesquisas para avaliar o funcionamento dos vários coeficientes de confiabilidade com mais complexas estruturas multidimensionais (Reise, 2012; Verde e Yang, 2015) e na presença de ordinais e/ou dados categóricos em que a não-conformidade com a suposição de normalidade é a norma.
conclusão
quando as pontuações totais dos ensaios são normalmente distribuídas (i.e.,, todos os itens são normalmente distribuídos) ω deve ser a primeira escolha, seguido Por α, UMA vez que eles evitam os problemas de sobrestimação apresentados pelo GLB. No entanto, quando houver um baixo ou moderado teste de skewness GLBa deve ser usado. Recomenda-se o GLB quando a proporção de itens assimétricos é elevada, uma vez que nestas condições o uso de α e ω como estimadores de fiabilidade não é aconselhável, qualquer que seja o tamanho da amostra.
contribuições do autor
desenvolvimento da ideia de pesquisa e estrutura teórica (it, JA). Construção do quadro metodológico (it, JA)., Desenvolvimento da sintaxe da linguagem R (it, JA). Análise de dados e interpretação de dados (it, JA). Discussão dos resultados à luz do contexto teórico atual (JA, IT). Preparação e escrita do artigo (JA, IT). Em geral, ambos os autores contribuíram igualmente para o desenvolvimento deste trabalho.,o primeiro autor divulgou o recebimento do seguinte apoio financeiro para a pesquisa, autoria e/ou publicação deste artigo: recebeu apoio financeiro da Comissão Nacional de pesquisa científica e tecnológica (CONICYT) “Becas Chile” Doctoral Fellowship program (Grant no: 72140548).
Declaração de conflito de interesses
os autores declaram que a investigação foi realizada na ausência de quaisquer relações comerciais ou financeiras que possam ser interpretadas como um potencial conflito de interesses.
Cronbach, L. (1951)., Coeficiente alfa e estrutura interna dos ensaios. Psychometrika 16, 297-334. doi: 10.1007 / BF02310555
CrossRef Full Text/Google Scholar
McDonald, R. (1999). Test Theory: a Unified Treatment. Mahwah, NJ: Lawrence Erlbaum Associates.
Google Scholar
R Development Core Team (2013). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Raykov, T. (1997)., Scale reliability, cronbach”s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package “psych.,”Available online at: http://org/r/psych-manual.pdf
Shapiro, A., and ten Berge, J. M. F. (2000). O viés assintótico da análise mínima do fator vestigial, com aplicações para o maior limite inferior à confiabilidade. Psychometrika 65, 413-425. Doi: 10.1007/BF02296154
CrossRef Full Text | Google Scholar
ten Berge, J. M. F., And Sočan, G. (2004). O maior limite inferior à confiabilidade de um teste e à hipótese de unidimensionalidade. Psychometrika 69, 613-625. doi: 10.,1007 / BF02289858
CrossRef Full Text | Google Scholar
Woodhouse, B., and Jackson, P. H. (1977). Limites inferiores para a fiabilidade da pontuação total num teste composto por itens não homogéneos: II: um procedimento de pesquisa para localizar o limite inferior mais elevado. Psychometrika 42, 579-591. doi: 10.1007/BF02295980
CrossRef Full Text/Google Scholar
Appendix I
r syntax to estimate reliability coefficients from Pearson”s correlation matrices., A correlação de valores fora da diagonal são calculados multiplicando-se o fator de carregamento dos itens: (1) tau-modelo equivalente eles são todos iguais para 0.3114 (λiλj = 0.558 × 0.558 = 0.3114) e (2) congeneric modelo que variam em função de diferentes fator de carga (por exemplo, o elemento da matriz a1, 2 = λ1λ2 = 0.3 × 0.4 = 0.12). Em ambos os exemplos, a verdadeira fiabilidade é 0,731.
> omega(Cr,1)$alpha # padronizado Cronbach’s α
0.731
> omega(Cr,1)$omega.tot # coefficient ω total
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach”s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731