
Pitágoras
Mais de 2000 anos atrás, houve uma descoberta incrível sobre triângulos:
Quando um triângulo tem um ângulo reto (90°) …
… e Quadrados são feitos em cada um dos três lados …
… então o maior quadrado tem a mesma área que os outros dois quadrados juntos!,
Ele é chamado de “teorema de Pitágoras” Teorema” e pode ser escrito em um curto equação:
a2 + b2 = c2
Nota:
- c é o maior lado do triângulo
- a e b são os outros dois lados
Definição
O maior lado do triângulo é chamado de o “hipotenusa”, de modo que a definição formal é:
Em um ângulo direito do triângulo:
o quadrado da hipotenusa é igual a
a soma dos quadrados dos outros dois lados., claro … ?
vamos ” ver se realmente funciona usando um exemplo.

porque é que isto é útil?
se soubermos o comprimento de dois lados de um triângulo com ângulo direito, podemos encontrar o comprimento do terceiro lado. (Mas lembre-se que só funciona em triângulos de ângulo direito!)
como usá-lo?,
o Escrever como uma equação:
 |
a2 + b2 = c2 |
em Seguida, vamos usar a álgebra de encontrar qualquer valor em falta, como nestes exemplos:
Você também pode ler sobre Quadrados e Raízes Quadradas, para descobrir por √169 = 13
Ele funciona de outra maneira, também: quando os três lados de um triângulo tornar a2 + b2 = c2, então o triângulo é o ângulo direito.,
e você mesmo pode provar o teorema !
obter caneta e tesouras de papel, em seguida, usando a seguinte animação como um guia:
- desenhar um triângulo inclinado direito no papel, deixando muito espaço.,
- Desenhar um quadrado ao longo da hipotenusa (lado maior)
- Desenhar com o mesmo tamanho praça do outro lado da hipotenusa
- Desenhar linhas, como mostrado na animação, como este:

- Corte as formas
- Organizá-los de modo que você pode provar que o quadrado grande tem a mesma área que os dois quadrados sobre os lados
o Outro, Surpreendentemente Simples, Prova
Aqui é uma das mais antigas provas de que o quadrado sobre o lado mais longo tem a mesma área, como em outras praças.,
observe a animação, e preste atenção quando os triângulos começam a deslizar ao redor.
Você pode querer assistir a animação algumas vezes para entender o que está acontecendo.o triângulo roxo é o importante.
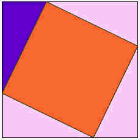 |
fica | 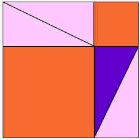 |

