8.1 Um exemplo histórico
Em seu livro, A Duas Novas Ciências, Galileu Galileia (1564-1642) dá vários argumentos, demonstrar que não pode haver tal coisa como real infinitos reais ou infinitesimais. Um de seus argumentos pode ser reconstruído da seguinte forma. Galileu propõe que tomemos como premissa que existe uma infinidade real de Números Naturais (os números naturais são os números inteiros positivos a partir de 1 em diante):
{1, 2, 3, 4, 5, 6, 7, ….,}
ele também propõe que tomemos como premissa que existe uma infinidade real dos quadrados dos números naturais.
{1, 4, 9, 16, 25, 36, 49, ….}
Agora, razões Galileu, note que estes dois grupos (hoje nós os chamaríamos de “conjuntos”) têm o mesmo tamanho. Podemos ver isso porque podemos ver que existe uma correspondência de um para um entre os dois grupos.,
| {1, | 2, | 3, | 4, | 5, | 6, | 7, ….,div> | |
| {1, | 4, | 9, | 16, | 25, | 36, | 49, …} |
Se a gente pode associar a cada número natural com um e somente um número quadrado, e se podemos associar a cada número quadrado com um e somente um número natural, então estes conjuntos devem ser do mesmo tamanho.,mas espere um momento, diz Galileu. Há, obviamente, muito mais números naturais do que números quadrados. Isto é, cada número quadrado está na lista de números naturais, mas muitos dos números naturais não estão na lista de números quadrados. Os seguintes números estão todos na lista de números naturais, mas não na lista de números quadrados.
{2, 3, 5, 6, 7, 8, 10, ….,}
assim, por razões de Galileu, se há muitos números no grupo dos números naturais que não estão no grupo dos números quadrados, e se não há números no grupo dos números quadrados que não estão nos números naturais, então os números naturais são maiores do que os números quadrados. E se o grupo dos números naturais é maior que o grupo dos números quadrados, então os números naturais e os números quadrados não são do mesmo tamanho.,
chegamos a duas conclusões: o conjunto dos números naturais e o conjunto dos números em quadrados do mesmo tamanho; e, o conjunto dos números naturais e o conjunto dos números em quadrados não são do mesmo tamanho. Isso é contraditório.
Galileu argumenta que a razão pela qual chegamos a uma contradição é porque assumimos que existem infinidades reais. Conclui, portanto, que não existem infinidades reais.
8.2 provas Indiretas
nossa lógica ainda não é forte o suficiente para provar alguns argumentos válidos. Considere o seguinte argumento como um exemplo.,
(P→(QvR))
Q
R
P
Este argumento parece válido. Pela primeira premissa sabemos: se P fosse verdadeiro, então (Q v R) seria verdadeiro. Mas então Q ou R ou ambos seriam verdade. E pela segunda e terceira premissas sabemos: Q é falso E R é falso. Assim, não pode ser que (Q v R) seja verdade, e assim não pode ser que P seja verdade.
Podemos verificar o argumento usando uma tabela verdade. A nossa mesa será complexa porque uma das nossas premissas é complexa.,
In any kind of situation in which all the premises are true, the conclusion is true., Isto é: as premissas são todas verdadeiras apenas na última fila. Para essa linha, a conclusão também é verdadeira. Então, este é um argumento válido.
mas demore um minuto e tente provar este argumento. Nós começar com

E agora estamos parados. Não podemos aplicar nenhuma das nossas regras. Aqui está um argumento válido de que não fizemos nosso sistema de raciocínio forte o suficiente para provar.existem várias formas de corrigir este problema e de tornar o nosso sistema de raciocínio suficientemente forte., Uma das soluções mais antigas é introduzir um novo método de prova, tradicionalmente chamado “reductio ad absurdum”, o que significa uma redução ao absurdo. Este método também é muitas vezes chamado de “prova indireta” ou “derivação indireta”.
A idéia é que nós assumimos a negação de nossa conclusão, e então mostrar que uma contradição resulta. Uma contradição é mostrada quando provamos alguma sentença Ψ, e sua negação Ψ. Isto pode ser qualquer frase. O ponto é que, dado o princípio da bivalência, devemos ter provado algo falso. Pois Se Ψ é verdadeiro, então Ψ é falso; E Se Ψ é verdadeiro, então Ψ é falso., Nós não precisamos saber o que é falso (Ψ Ou Ψ); é suficiente saber que um deles deve ser.
lembre-se que nós construímos o nosso sistema lógico para que ele não possa produzir uma falsidade a partir de afirmações verdadeiras. A fonte da falsidade que produzimos na derivação indireta deve, portanto, ser alguma falsidade que acrescentamos ao nosso argumento. E o que acrescentamos ao nosso argumento é a negação da conclusão. Assim, a conclusão deve ser verdadeira.,
A forma do argumento é a seguinte:

Tradicionalmente, o pressuposto para a derivação indireta também tem sido comumente chamado de “o pressuposto para a reductio”.como exemplo concreto, podemos provar o nosso caso de perplexidade.

assumimos a negação da nossa conclusão na Linha 4. A conclusão que acreditávamos que estava correta era P, e a negação disto é P. na linha 7, provamos R., Tecnicamente, terminámos nessa altura, mas gostaríamos de ser gentis com qualquer um que tentasse compreender a nossa prova, por isso repetimos a linha 3 para que as frases R E R estejam lado a lado, e é muito fácil ver que algo correu mal. Isto é, se provamos tanto R como R, então provamos algo falso.o nosso raciocínio agora é assim. O que correu mal? A linha 8 é um uso correto de repetição; a linha 7 vem de um uso correto de modus tollendo ponens; a linha 6 de um uso correto de modus ponens; a linha 5 de um uso correto de negação dupla., Portanto, não cometemos um erro no nosso raciocínio. Usámos as linhas 1, 2 e 3, mas essas são premissas que concordámos assumir que estão correctas. Isto deixa a Linha 4. Essa deve ser a fonte da minha contradição. Deve ser falso. Se a Linha 4 é falsa, então P é verdadeiro.algumas pessoas consideram as provas indiretas menos fortes do que as provas diretas. Há muitas e complexas razões para isso. Mas, pela nossa lógica proposicional, nenhuma destas razões se aplica. Isto porque é possível provar que nossa lógica proposicional é consistente., Isto significa que é possível provar que a nossa lógica proposicional não pode provar uma falsidade a menos que se introduza primeiro uma falsidade no sistema. (Geralmente não é possível provar que sistemas lógicos ou matemáticos mais poderosos e avançados são consistentes, a partir de dentro desses sistemas; por exemplo, não se pode provar em aritmética que a aritmética é consistente. Dado que podemos estar certos da consistência da lógica proposicional, podemos estar certos de que em nossa lógica proposicional uma prova indireta é uma boa forma de raciocínio., Sabemos que, se provarmos a falsidade, devemos ter introduzido a falsidade; e se estivermos confiantes em todas as outras suposições (isto é, as premissas) de nossa prova, exceto a suposição de derivação indireta, então podemos estar confiantes de que esta suposição de derivação indireta deve ser a fonte da falsidade.
uma nota sobre terminologia é necessária aqui. A palavra “contradição” é usada de forma ambígua na maioria das discussões lógicas. Pode significar uma situação como vemos acima, onde duas sentenças são afirmadas, e essas sentenças não podem ser ambas verdadeiras., Ou pode significar uma única frase que não pode ser verdade. Um exemplo de tal frase é (P^P)., A tabela verdade desta frase é:
| P | P | (P ^ P) |
|---|---|---|
| T | F | F |
| F | T | F |
Assim, esse tipo de frase pode nunca ser verdadeira, independentemente do significado de P.,
para evitar ambiguidades, neste texto, sempre chamaremos uma única frase que não pode ser verdadeira uma “frase contraditória”. Assim, (P^P) é uma frase contraditória. Situações em que duas sentenças são afirmadas que não podem ser ambas verdadeiras serão chamadas de “contradição”.
8.3 nosso exemplo, e outros exemplos
podemos reconstruir uma versão do argumento de Galileu agora. Usaremos a seguinte chave.
P: existem infinidades reais (incluindo os números naturais e os números quadrados).,
Q: Existe uma correspondência de um para um entre os números naturais e os números quadrados.
r: o tamanho do conjunto dos números naturais e o tamanho do conjunto dos números quadrados são os mesmos.
S: todos os números quadrados são números naturais.
T: alguns dos números naturais não são números quadrados.
U: há mais números naturais do que números quadrados.,
Com esta chave, o argumento será traduzido:
(P→Q)
(Q→R)
(P→(S^T))
((S^T)→U)
(U→R)
P
E podemos provar este é um argumento válido usando indireta derivação:

Na linha 6, partimos do pressuposto de P porque Galileu acreditava que P e teve como objetivo provar que a P. Que é, ele acredita que não há real infinitos, e então assumido que era falso acreditar que não é o caso que não existem efetivamente infinitos. Esta falsidade levará a outras falsidades, expondo-se.,
para os interessados: Galileu concluiu que não existem infinidades reais, mas existem infinidades potenciais. Assim, ele argumentou, não é o caso de que todos os números naturais existem (em algum sentido de “existir”), mas é verdade que você poderia contar números naturais para sempre. Muitos filósofos antes e depois de Galileu defenderam esta visão; é semelhante a uma visão defendida por Aristóteles, que era um importante lógico e filósofo escrevendo quase dois mil anos antes de Galileu.,
Note que em um argumento como este, você poderia raciocinar que não a suposição para derivação indireta, mas sim uma das premissas era a fonte da contradição. Hoje, a maioria dos matemáticos acredita nisso sobre o argumento de Galileu. Um lógico e matemático chamado Georg Cantor (1845-1918), o inventor da teoria dos conjuntos, argumentou que conjuntos infinitos podem ter subconjuntos próprios do mesmo tamanho., Isto é, Cantor negou a premissa 4 acima: embora todos os números quadrados sejam números naturais, e nem todos os números naturais são números quadrados, não é o caso que estes dois conjuntos são de tamanho diferente. Cantor aceitou no entanto a premissa 2 acima, e, portanto, acreditava que o tamanho do conjunto de Números Naturais e o tamanho do conjunto de números quadrados é o mesmo. Hoje, usando o raciocínio de Cantor, matemáticos e lógicos estudam o infinito, e desenvolveram um grande corpo de conhecimento sobre a natureza do infinito. Se isto lhe interessa, veja a secção 17.5.,consideremos outro exemplo para ilustrar a derivação indirecta. Um conjunto muito útil de teoremas são hoje chamados “Teoremas de Morgan”, em homenagem ao lógico Augustus De Morgan (1806-1871). Não podemos afirmar plenamente, até o capítulo 9, mas podemos afirmar que os seus equivalentes em inglês: DeMorgan observado que (PvQ) e (P^Q) são equivalentes, e também que (P^Q) e (PvQ) são equivalentes. Dado isto, deve ser um teorema de nossa linguagem que (PvQ)→(P^Q)). Vamos provar isto.
A fórmula inteira é condicional, então vamos usar uma derivação condicional., Nossa prova deve assim começar:
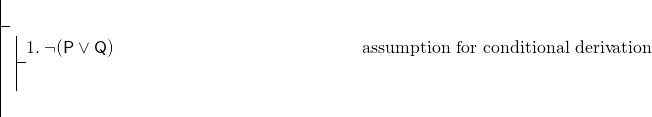
para completar a derivação condicional, devemos provar (P^Q). Esta é uma conjunção, e a nossa regra para mostrar conjunções é a adjunção. Uma vez que usar esta regra pode ser a nossa melhor maneira de mostrar (P^Q), podemos apontar para mostrar P e, em seguida, mostrar Q, e, em seguida, executar adjunção. Mas, obviamente, temos muito pouco com que trabalhar – apenas a linha 1, que é uma negação. Em tal caso, é tipicamente sábio tentar uma prova indireta. Começa com uma prova indirecta de P.,

agora precisamos encontrar uma contradição, qualquer contradição. Mas já há uma óbvia. A linha 1 diz que nem P nem Q é verdade. Mas a linha 3 diz que P é verdade. Temos de tornar esta contradição explícita, encontrando uma fórmula e a sua negação. Podemos fazer isto com adição.

para completar a prova, vamos usar esta estratégia novamente.

iremos provar os teoremas de Morgan como problemas para o Capítulo 9.,
Aqui está uma regra geral para fazer provas: ao provar uma derivação condicional, sempre faça derivação condicional; caso contrário, tente derivação direta; se isso falhar, então, tente derivação indireta.
8.4 problemas
- Complete as seguintes provas. Cada um exigirá uma derivação indireta. Os últimos dois são desafiadores.
- Prove os seguintes teoremas.
- (P^P).
- ((P→P)^(P→P)).
- (P→(P^Q)).
- ((P^Q)→(P→Q)).
- Em inglês coloquial normal, escreva o seu próprio argumento válido com pelo menos duas premissas., Seu argumento deve ser apenas um parágrafo (não uma lista ordenada de sentenças ou qualquer outra coisa que se pareça com lógica formal). Traduza-o em lógica proposicional e prove que é válido usando uma derivação indireta.
Esta tradução do título do livro de Galileu tornou-se a mais comum, embora uma mais literal teria sido discursos matemáticos e demonstrações. As traduções do livro incluem Drake (1974).