“eu estou convencido que Ele não jogue dados.,”
~ Albert Einstein
- Variáveis Aleatórias
- Discreta Variáveis Aleatórias
- Contínuo de Variáveis Aleatórias
- Misto de Variáveis Aleatórias
- Funções de Distribuição Cumulativa (CDF)
- Função de Densidade de Probabilidade (PDF)
- Interativo CDF/PDF Exemplo
Variáveis Aleatórias:

Dizer que você estava para levar uma moeda de seu bolso e de lançá-lo no ar. Enquanto ele gira através do espaço, o que você poderia dizer sobre o seu futuro?vai aterrar de cabeça erguida? Coroa?, Mais do que isso, quanto tempo vai ficar no ar? Quantas vezes vai saltar? A que distância de onde chega ao chão, vai finalmente descansar? Já agora, alguma vez vai cair no chão? Já Vieste descansar?
para algumas dessas questões, podemos e podemos estabelecer-nos em Respostas muito antes das observações; temos quase a certeza de que a gravidade vai aguentar e a moeda vai pousar. Mas, para os outros, não temos outra alternativa senão julgar e falar em termos mais vagos, se quisermos dizer alguma coisa de útil sobre o futuro.,como cientistas, é nosso trabalho dizer algo útil (ou, no mínimo, autoritário…), enquanto as moedas metafóricas de importante sistema físico ainda estão no ar. Cara ou coroa pode até ser uma questão de vida ou morte. As nossas moedas podem ser, por exemplo, vários caudais de fluido de arrefecimento ou massas de urânio numa central nuclear. Preocupamo-nos muito em saber quais são as nossas hipóteses de conseguirmos turbinas em vez de uma fusão.,
para um determinista rigoroso, todas essas apostas foram liquidadas muito antes de qualquer moeda, metafórica ou não, ter sido cunhada; simplesmente ainda não sabemos. Se ao menos soubéssemos as forças aplicadas no lançamento de uma moeda, a sua distribuição exacta da massa, os vários movimentos mínimos de ar na sala… Se soubéssemos tudo isso, saberíamos que o lançamento da moeda tinha 100% de hipóteses de aterrar da forma que aterrasse, e nenhuma hipótese de qualquer outro resultado.
mas nós, é claro, estamos muitas vezes sem uma fração mencionável de tal conhecimento do mundo., Além disso, parece em escalas excessivamente pequenas que deterministas estritos estão absolutamente errados; não há maneira de prever quando, por exemplo, um átomo de urânio irá se dividir, e se tal evento afeta o mundo maior, então esse evento macro é verdadeiramente imprevisível. Alguns resultados realmente estão no ar, perturbados até que façam parte do passado.
A fim de lidar com esta realidade e ser capaz de descrever os futuros Estados de um sistema de alguma forma útil, usamos variáveis aleatórias., Uma variável aleatória é simplesmente uma função que relaciona cada resultado físico possível de um sistema a um número real único. Como tal, existem três tipos de variáveis aleatórias: discreta, contínua e mista. Nas secções seguintes, estas categorias serão brevemente discutidas e serão apresentados exemplos.
variáveis aleatórias discretas:
considere o nosso lançamento da moeda novamente. Poderíamos ter cabeças ou caudas como possíveis resultados. Se definirmos uma variável, x, como o número de cabeças em um único arremesso, então x poderia possivelmente ser 1 ou 0, nada mais., Tal função, x, seria um exemplo de uma variável aleatória discreta. Tais variáveis aleatórias só podem assumir valores discretos. Outros exemplos seriam os possíveis resultados de um teste de gravidez, ou o número de alunos em uma sala de aula.
variáveis aleatórias contínuas:
de volta ao lançamento da moeda, e se desejássemos descrever a distância entre onde a nossa moeda veio a repousar e onde bateu pela primeira vez no chão. Essa distância, x, seria uma variável aleatória contínua porque poderia assumir um número infinito de valores dentro da Gama contínua de números reais., A moeda pode viajar 1 cm, ou 1,1 cm, ou 1,11 cm, ou entre e entre. Outros exemplos de variáveis aleatórias contínuas seriam a massa de estrelas em nossa galáxia, o pH das águas oceânicas, ou o tempo de residência de algum analito em um cromatógrafo gasoso.
variáveis aleatórias mistas:
variáveis aleatórias mistas têm componentes discretos e contínuos. Tais variáveis aleatórias são encontradas com pouca frequência. Para um possível exemplo, no entanto, você pode estar medindo o peso de uma amostra e decidir que qualquer peso medido como um valor negativo será dado um valor de 0., Dessa forma, a variável aleatória tem um componente discreto A x = 0 e componente contínuo onde x > 0.
funções de distribuição cumulativa (CDF):
a questão, é claro, surge sobre como descrever matematicamente (e visualmente exibir) variáveis aleatórias. Para essas tarefas, usamos funções de densidade de probabilidade (PDF) e funções de densidade cumulativa (CDF). Como os CDFs são mais simples de compreender para variáveis aleatórias discretas e contínuas do que PDFs, vamos primeiro explicar CDFs.
considere lançar um dado justo com 6 lados., Nós teríamos uma chance de 1 em 6 de obter qualquer um dos valores possíveis da variável aleatória (1, 2, 3, 4, 5, ou 6). Se nós plotarmos esses valores possíveis no eixo x e plotarmos a probabilidade de medir cada valor específico, x, ou qualquer valor menor que x no eixo y, teremos o CDF da variável aleatória.
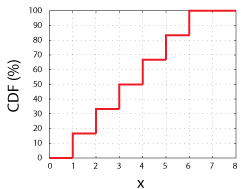
CDF para um dado Justo Com 6 lados. Note que cada passo é uma altura de 16,67%, ou 1 em 6.
Esta função, CDF(x), simplesmente nos diz as probabilidades de medir qualquer valor até e incluindo X., Como tal, todos os CDF devem ter estas características:
- um CDF deve igual a 0 quando x= -∞, e aproximação 1 (ou 100%) quando x se aproxima +∞. Simplificando, de todos os resultados possíveis, deve haver um resultado; a chance de lançar um dado de seis lados e obter um valor entre -∞ e ∞ é de 100%.
- o declive de um CDF deve ser sempre igual ou superior a zero. Por exemplo, considere a chance de lançar um dado de 6 lados (justo ou não) e obter um valor entre 0 e 4., Essa chance não pode ser mais do que a chance de obter um valor entre 0 e 5, porque as chances de um 1, 2, ou 3 aterrissagem viradas para cima são, é claro, sempre vai ser uma fração das chances de obter um 1, 2, 3, ou 4.
para um exemplo de uma variável aleatória contínua, a seguinte applet mostra o CDF normalmente distribuído.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Basta notar que as características de um CDF descrito acima e explicado para uma variável aleatória discreta hold para variáveis aleatórias contínuas também.
para exemplos mais intuitivos das propriedades dos CDFs, veja o exemplo interativo abaixo. Além disso, gráficos interativos de muitos outros CDFs importantes para o campo de estatísticas e usados neste site podem ser encontrados aqui.
Probability Density Functions (PDF):
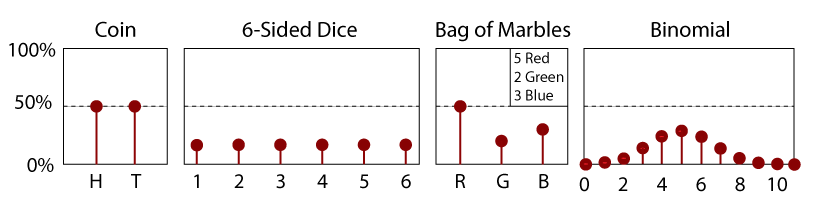
PDF for a Fair 6-Sidded Dice.
A PDF é simplesmente a derivada de um CDF., Assim, um PDF é também uma função de uma variável aleatória, x, e sua magnitude será alguma indicação da probabilidade relativa de medir um determinado valor. Como é a inclinação de um CDF, um PDF deve ser sempre positivo; não há probabilidades negativas para qualquer evento. Além disso, e por definição, a área sob a curva de um PDF(x) entre -∞ e x é igual ao seu CDF(x). Como tal, a área entre dois valores x1 e x2 dá a probabilidade de medir um valor dentro desse intervalo.
a seguinte applet mostra um exemplo do PDF para uma variável aleatória normalmente distribuída, X.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., também considere a diferença entre um PDF contínuo e discreto. Enquanto um PDF discreto (como o mostrado acima para Dados) lhe dará as chances de obter um resultado particular, probabilidades com PDFs contínuos são questões de alcance, Não pontos discretos. Por exemplo, há claramente uma chance de 1 em 6 (16,6%) de rolar um 3 em um dado, como pode ser visto em seu PDF. Mas qual é o estranho de medir exatamente zero com uma variável aleatória com um PDF normal e média de zero, como mostrado acima? Embora seja o valor onde o PDF é o maior, a chance de medir exatamente 0,00000..,. é, talvez contra intuitivamente, zero. As probabilidades de medir qualquer número aleatório em particular para uma precisão infinita são, de facto, zero. com um PDF contínuo você pode, em vez disso, perguntar quais são as probabilidades que você vai medir entre dois valores para obter uma probabilidade que é maior do que zero. Para encontrar essa probabilidade nós simplesmente usamos o CDF de nossa variável aleatória., Porque o CDF nos conta o estranho de medição de um valor ou qualquer coisa menor do que esse valor, para encontrar a probabilidade de medição entre dois valores, x1 e x2 (onde x1 > x2), basta tomar o valor de FCD em x1 e subtrair o valor da CDF em x2. Por exemplo, usando o CDF normal no applet acima (com μ=0 e σ=1), se quiséssemos conhecer as probabilidades de medição entre 0,01 e 0,02 encontramos CDF(x=0.1)=53.9828% e CDF(x=0.2)=57.9260%. Em seguida, a diferença, CDF(0,2)-CDF(0,1), nos dá a probabilidade de cerca de 3,9% de medir um x entre 0,1 e 0,2., para exemplos visuais mais intuitivos das propriedades de PDFs, veja o exemplo interativo abaixo. Além disso, gráficos interativos de muitos PDFs importantes usados neste site podem ser vistos aqui. |
|||||||||||||||||