α coeficient este cel mai utilizat pe scară largă de proceduri pentru estimarea fiabilității în cercetarea aplicată. După cum a declarat Sijtsma (2009), popularitatea sa este de așa natură încât Cronbach (1951) a fost citat ca referință mai frecvent decât articolul despre descoperirea ADN-ului dublu helix., Cu toate acestea, limitările sale sunt bine cunoscute (Lord și Novick, 1968; Cortina, 1993; Yang și Green, 2011), unele dintre cele mai importante fiind ipotezele erorilor necorelate, tau-echivalența și normalitatea.
ipoteza necorelate erori (eroare scor de orice pereche de elemente este necorelat) este o ipoteză de Test Clasic de Teorie (Domnul și Novick, 1968), încălcarea care poate sugera prezența de complexe, multidimensionale structuri care necesită proceduri de estimare care să ia această complexitate în considerare (de exemplu, Tarkkonen și Vehkalahti, 2005; Verde și Yang, 2015)., Este important să se dezrădăcineze credința eronată că coeficientul α este un bun indicator al unidimensionalității, deoarece valoarea sa ar fi mai mare dacă scara ar fi unidimensională. De fapt, exact opusul este cazul, așa cum a arătat Sijtsma (2009), iar aplicarea sa în astfel de condiții poate duce la supraestimarea fiabilității (Raykov, 2001). În consecință, înainte de calcularea α este necesar să se verifice dacă datele se potrivesc modelelor unidimensionale.
ipoteza echivalenței tau (adică.,, același scor adevărat pentru toate elementele de testare sau încărcări egale ale tuturor elementelor dintr-un model factorial) este o cerință ca α să fie echivalent cu coeficientul de fiabilitate (Cronbach, 1951). Dacă ipoteza echivalenței tau este încălcată, valoarea reală a fiabilității va fi subestimată (Raykov, 1997; Graham, 2006) cu o sumă care poate varia între 0,6 și 11,1% în funcție de gravitatea încălcării (Green și Yang, 2009a). Lucrul cu date care respectă această ipoteză nu este, în general, viabil în practică (Teo și Fan, 2013); modelul congeneric (adică.,, diferite sarcini factor) este mai realist.
cerința pentru normalitatea multivariantă este mai puțin cunoscută și afectează atât estimarea fiabilității puntuale, cât și posibilitatea stabilirii intervalelor de încredere (Dunn et al., 2014). Sheng și Sheng (2012) a observat recent că, atunci când distribuțiile sunt asimetrice și/sau leptocurtice, o polarizare negativă este produsă atunci când coeficientul α se calculează; rezultate similare au fost prezentate de Verde și Yang (2009b) într-o analiză a efectelor non-distribuții normale în estimarea fiabilității., Studiul problemelor de înclinare este mai important atunci când vedem că, în practică, cercetătorii lucrează în mod obișnuit cu scale înclinate (Micceri, 1989; Norton et al., 2013; Ho și Yu, 2014). De exemplu, Micceri (1989) a estimat că aproximativ 2/3 din capacitate și peste 4/5 din măsurile psihometrice au prezentat o asimetrie cel puțin moderată (adică o înclinare în jurul valorii de 1). În ciuda acestui fapt, impactul skewness asupra estimării fiabilității a fost puțin studiat.,
având în Vedere abundente literatura de specialitate cu privire la limitările și prejudecățile de α coeficient (Revelle și Zinbarg, 2009; Sijtsma, 2009, 2012; Cho și Kim, 2015; Sijtsma și van der Arca, 2015), apare întrebarea de ce cercetatorii continua să utilizați α, atunci când alternativă coeficienți care există depăși aceste limitări. Este posibil ca excesul de proceduri de estimare a fiabilității dezvoltat în ultimul secol a oscured dezbaterea. Acest lucru ar fi fost agravată în continuare de simplitatea calculării acestui coeficient și disponibilitatea acestuia în software-uri comerciale.,
dificultatea estimării pxx’ coeficientul de fiabilitate locuiește în definiția sa pxx’=σt2∕σx2, care include adevărat scorul în varianța numărător atunci când acest lucru este prin natura neobservabile. Coeficientul α încearcă să aproximeze această variație neobservabilă de covarianța dintre elemente sau componente. Cronbach (1951) a arătat că, în absența tau-echivalență, coeficientul α (sau Guttman”s lambda 3, care este echivalent cu α) a fost o bună aproximare limită inferioară., Astfel, atunci când ipotezele sunt încălcate problema se traduce în găsirea celor mai bune limita inferioară; într-adevăr, acest nume este dat de cea mai Mare limită Inferioară metoda (GLB) care este cea mai bună aproximare de un teoretice unghi (Jackson și Agunwamba, 1977; Woodhouse și Jackson, 1977; Shapiro și ten Berge, 2000; Sočan, 2000; ten Berge și Sočan, 2004; Sijtsma, 2009). Cu toate acestea, Revelle și Zinbarg (2009) consideră că ω oferă o limită inferioară mai bună decât GLB., Prin urmare, există o dezbatere nerezolvată cu privire la care dintre aceste două metode oferă cea mai bună limită inferioară; în plus, problema non-normalității nu a fost investigată exhaustiv, așa cum se discută în prezenta lucrare.
ω Coeficienții
McDonald (1999) a propus wt coeficientul de estimare a fiabilității de la o analiză factorială cadru, care poate fi exprimată în mod oficial ca:
Unde λj este de încărcare a elementului j, λj2 este comuniune de elementul j și ψ echivaleaza cu unicitatea., Coeficientul wt, prin includerea Lambda-urilor în formulele sale, este adecvat atât atunci când există tau-echivalență (adică încărcări egale ale tuturor elementelor de testare) (wt coincide matematic cu α), cât și atunci când elementele cu discriminări diferite sunt prezente în reprezentarea construcției (adică încărcări diferite ale elementelor: măsurători congenerice). În consecință, wt corectează prejudecata de subestimare a α atunci când ipoteza echivalenței tau este încălcată (Dunn et al., 2014) și diferite studii arată că este una dintre cele mai bune alternative pentru estimarea fiabilității (Zinbarg et al.,, 2005, 2006; Revelle și Zinbarg, 2009), deși până în prezent funcționarea sa în condiții de înclinare nu este cunoscută.
atunci Când există o corelație între erori, sau există mai mult de o dimensiune latentă în date, contribuția fiecărui dimensiune totală varianța explicată este estimat, obținând așa-numitele ierarhic ω (wh), care ne permite pentru a corecta cel mai rău supraestimarea de polarizare α cu date multidimensionale (a se vedea Tarkkonen și Vehkalahti, 2005; Zinbarg et al., 2005; Revelle și Zinbarg, 2009)., Coeficienții wh și wt sunt echivalenți în date unidimensionale, deci ne vom referi la acest coeficient pur și simplu ca ω.
cea mai Mare limită Inferioară (GLB)
Sijtsma (2009) arată într-o serie de studii care una dintre cele mai puternice estimatori de fiabilitate este GLB—a dedus de Woodhouse și Jackson (1977) de la ipotezele Clasice de Testare Teorie (Cx = Ct + Ce)—o inter-itemi matricea de covarianta pentru observate item Cx. Se descompune în două părți: suma matricei de covarianță inter-item pentru item true scores Ct; și matricea de covarianță de eroare inter-item ce (ten Berge și Sočan, 2004)., Expresia sa este:
în cazul în care σx2 este testul de varianță și tr(Ce) se referă la urma de inter-element de eroare matricei de covarianță, care s-a dovedit atât de dificil de estimat. O soluție a fost utilizarea procedurilor factoriale, cum ar fi analiza factorului de rang minim (o procedură cunoscută sub numele de glb.fa). Mai recent, procedura algebrică GLB (GLBa) a fost dezvoltată dintr-un algoritm conceput de Andreas Moltner (Moltner și Revelle, 2015)., Potrivit Revelle (2015a) această procedură se adoptă forma care este cel mai fidel originalului definiție de Jackson și Agunwamba (1977), și are avantajul de a introduce un vector de greutate elementele de importanță (Al-Homidan, 2008).în ciuda punctelor sale forte teoretice, GLB a fost foarte puțin utilizat, deși unele studii empirice recente au arătat că acest coeficient produce rezultate mai bune decât α (Lila et al., 2014) și α și ω (Wilcox et al., 2014)., Cu toate acestea, în eșantioane mici, în ipoteza normalității, tinde să supraestimeze valoarea reală a fiabilității (Shapiro și ten Berge, 2000); cu toate acestea, funcționarea sa în condiții non-normale rămâne necunoscută, în special atunci când distribuțiile elementelor sunt asimetrice.având în vedere coeficienții definiți mai sus și prejudecățile și limitările fiecăruia, obiectul acestei lucrări este de a evalua robustețea acestor coeficienți în prezența elementelor asimetrice, luând în considerare și ipoteza tau-echivalenței și a mărimii eșantionului.,
Metode
Generarea de Date
datele au fost generate folosind R (R Dezvoltarea Echipei de Bază, 2013) și RStudio (Racine, 2012) software-ul, după modelul factorial:
în cazul în care Xij este simulat de răspuns a subiectului i din elementul j, λjk este de încărcare a elementului j în Factorul k (care a fost generat de s model); Fk este factor latent generat de o distribuție normală normată (în medie 0 și varianță 1), ej este aleatoare de măsurare eroare de fiecare element, de asemenea, urmează o distribuție normală normată.,
Denaturate elemente: Standard normal Xij au fost transformate pentru a genera non-distribuții normale folosind procedura propusă de Headrick (2002) aplicarea de al cincilea ordin polinomial transformă:
Simulate Condiții
Pentru a evalua performanța de fiabilitate coeficienții (α, ω, GLB și GLBa) am lucrat cu trei dimensiuni de probă (250, 500, 1000), testare două dimensiuni: scurt (6 itemi) și lung (12 articole), două condiții de tau-echivalența (una cu tau-echivalență și unul fără, adică,, congeneric) și încorporarea progresivă a elementelor asimetrice (de la toate elementele fiind normale la toate elementele fiind asimetrice). În scurt test de fiabilitate a fost stabilit la 0.731, care în prezența tau-echivalența este realizată cu șase elemente cu factor loadings = 0.558; în timp ce congenere model este obținut prin stabilirea factor loadings la valori de 0.3, 0.4, 0.5, 0.6, 0.7, și 0,8 (a se vedea Apendicele I). În testul lung de 12 elemente, fiabilitatea a fost stabilită la 0.,845 luând aceleași valori ca în testul scurt atât pentru tau-echivalența, cât și pentru modelul congeneric (în acest caz au existat două elemente pentru fiecare valoare a lambda). În acest fel au fost simulate 120 de condiții cu 1000 de replici în fiecare caz.
Analiza Datelor
principalele analize au fost efectuate folosind Psych (Revelle, 2015b) și GPArotation (Bernaards și Jennrich, 2015) pachete, care permite α și ω să fie estimată. Două abordări computerizate au fost utilizate pentru estimarea GLB: glb.fa (Revelle, 2015a) și glb.,algebric (Moltner și Revelle, 2015), acesta din urmă a lucrat de autori precum Hunt and Bentler (2015).pentru a evalua acuratețea diferiților estimatori în recuperarea fiabilității, am calculat pătratul Mediu rădăcină al erorii (RMSE) și părtinirea. Prima este media diferențelor dintre fiabilitatea estimată și cea simulată și este formalizată ca:
unde ρ^ este fiabilitatea estimată pentru fiecare coeficient, ρ fiabilitatea simulată și Nr numărul de replici., A % prejudecată este înțeles ca diferență între valoarea medie a estimat fiabilitate și simulate fiabilitatea și este definit ca:
În ambele indici, cea mai mare valoarea, cu atât mai mare inexactitate de estimator, dar spre deosebire de RMSE, prejudecată poate fi pozitiv sau negativ; în acest caz, informații suplimentare-ar fi obținut dacă coeficientul este subestimarea sau supraestimarea simulat fiabilitate parametru., În urma recomandării Hoogland și Boomsma (1998) valorile RMSE < 0,05 și % prejudecată < 5% au fost considerate acceptabile.
rezultate
rezultatele principale pot fi văzute în tabelul 1 (6 elemente) și Tabelul 2 (12 elemente). Acestea arată părtinirea RMSE și % a coeficienților în condiții de echivalență tau și congenerice și modul în care înclinarea distribuției testului crește odată cu încorporarea treptată a elementelor asimetrice.
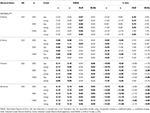
Tabelul 1., RMSE și Bias cu tau-echivalență și condiție congenerică pentru 6 articole, trei dimensiuni ale eșantionului și numărul de articole înclinate.
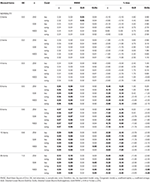
Tabelul 2. RMSE și Bias cu tau-echivalență și condiție congenerică pentru 12 articole, trei dimensiuni ale eșantionului și numărul de articole înclinate.
Numai în condiții de tau-echivalență și normalitate (skewness < 0.2) se observă că α coeficientul de estimări simulate fiabilitate corect, ca ω., În starea congenerică ω corectează subestimarea α. Atât GLB, cât și GLBa prezintă o tendință pozitivă în cadrul normalității, cu toate acestea, GLBa prezintă o tendință de aproximativ ½ % mai mică decât GLB (a se vedea tabelul 1). Dacă luăm în considerare dimensiunea eșantionului, observăm că, pe măsură ce mărimea testului crește, prejudecata pozitivă a GLB și GLBa se diminuează, dar nu dispare niciodată.
În asimetric condiții, vom vedea în Tabelul 1 că ambele α și ω prezent inacceptabil de performanță cu creșterea RMSE și subestimări care poate ajunge la bias > 13% pentru α coeficient (între 1 și 2% mai mici pentru ω)., Coeficienții GLB și GLBa prezintă un RMSE mai mic atunci când testul de înclinare sau numărul de elemente asimetrice crește (a se vedea tabelele 1, 2). Coeficientul GLB prezintă estimări mai bune atunci când valoarea de testare a testului este de aproximativ 0,30; GLBa este foarte asemănătoare, prezentând estimări mai bune decât ω, cu o valoare de testare în jurul valorii de 0,20 sau 0,30. Cu toate acestea, atunci când valoarea skewness crește la 0, 50 sau 0, 60, GLB prezintă performanțe mai bune decât GLBa. Dimensiunea testului (6 sau 12 ítems) are un efect mult mai important decât dimensiunea eșantionului asupra preciziei estimărilor.,
Discuții
În acest studiu a patru factori au fost manipulate: tau-de echivalență sau de congeneri modelul, dimensiunea eșantionului (250, 500 și 1000), numărul de elemente de testare (6 și 12) și numărul de elemente asimetrice (de la 0 asimetric articole la toate elementele fiind asimetric), în scopul de a evalua robustețea prezenței asimetrice de date în patru coeficienți de fiabilitate analizate. Aceste rezultate sunt discutate mai jos.,
în condiții de tau-echivalență, coeficienții α și ω converg, cu toate acestea, în absența tau-echivalență (congeneric), ω prezintă întotdeauna estimări mai bune și RMSE mai mici și % părtinire decât α. În acest mai realist starea aceea (Verde și Yang, 2009a; Yang și Verde, 2011), α devine un negativ părtinitoare fiabilitate estimator (Graham, 2006; Sijtsma, 2009; Cho și Kim, 2015) și ω este întotdeauna de preferat să α (Dunn et al., 2014). În cazul nerespectării presupunerii normalității, ω este cel mai bun estimator al tuturor coeficienților evaluați (Revelle și Zinbarg, 2009).,revenind la dimensiunea eșantionului, observăm că acest factor are un efect mic sub normalitate sau o ușoară abatere de la normalitate: RMSE și părtinirea se diminuează pe măsură ce mărimea eșantionului crește. Cu toate acestea, se poate spune că pentru acești doi coeficienți, cu dimensiunea eșantionului de 250 și normalitate obținem estimări relativ exacte (Tang și Cui, 2012; Javali et al., 2011)., Pentru GLB și GLBa coeficienți, în dimensiunea eșantionului crește RMSE și prejudecată tind să se diminueze; cu toate acestea se menține o prejudecată pozitivă pentru starea de normalitate, chiar și cu eșantioane de dimensiuni mari de 1000 (Shapiro și ten Berge, 2000; ten Berge și Sočan, 2004; Sijtsma, 2009).
pentru dimensiunea testului observăm în general o RMSE și o părtinire mai mare cu 6 articole decât cu 12, sugerând că cu cât numărul de articole este mai mare, cu atât RMSE este mai mic și părtinirea estimatorilor (Cortina, 1993). În general, tendința este menținută atât pentru 6, cât și pentru 12 articole.,
Când ne uităm la efectul progresiv încorporează elemente asimetrice în setul de date, observăm că α coeficient este extrem de sensibil la asimetrice elemente; aceste rezultate sunt similare cu cele găsite de Sheng și Sheng (2012) și Verde și Yang (2009b). Coeficientul ω prezintă valori similare RMSE și bias cu cele ale α, dar puțin mai bune, chiar și cu tau-echivalență. GLB și GLBa sunt găsite pentru a prezenta estimări mai bune atunci când testul skewness se îndepărtează de la valori apropiate de 0.având în vedere că în practică este comună găsirea datelor asimetrice (Micceri, 1989; Norton et al.,, 2013; Ho și Yu, 2014), sugestia Sijtsma (2009) de utilizare a GLB ca estimator de fiabilitate pare bine întemeiată. Alți autori, cum ar fi Revelle și Zinbarg (2009) și Verde și Yang (2009a), se recomanda utilizarea de ω, cu toate acestea acest coeficient produs numai bun rezultate în starea de normalitate, sau cu procent redus de asimetrie elemente. În orice caz, acești coeficienți au prezentat avantaje teoretice și empirice mai mari decât α. Cu toate acestea, recomandăm cercetătorilor să studieze nu numai estimări punctuale, ci și să utilizeze estimarea intervalului (Dunn et al., 2014).,aceste rezultate sunt limitate la condițiile simulate și se presupune că nu există o corelație între erori. Acest lucru ar face necesară efectuarea unor cercetări suplimentare pentru a evalua funcționarea diferiților coeficienți de fiabilitate cu structuri multidimensionale mai complexe (Reise, 2012; Green și Yang, 2015) și în prezența datelor ordinale și/sau categorice în care nerespectarea presupunerii normalității este norma.
concluzie
când scorurile totale ale testelor sunt distribuite în mod normal (adică.,, toate elementele sunt distribuite în mod normal) ω ar trebui să fie prima alegere, urmată de α, deoarece evită problemele de supraestimare prezentate de GLB. Cu toate acestea, atunci când există un test scăzut sau moderat skewness GLBa trebuie utilizat. GLB este recomandat atunci când proporția de elemente asimetrice este mare, deoarece în aceste condiții utilizarea atât α cât și ω ca estimatori de fiabilitate nu este recomandabilă, indiferent de dimensiunea eșantionului.dezvoltarea ideii de cercetare și a cadrului teoretic (IT, JA). Construcția cadrului metodologic (IT, JA)., Dezvoltarea sintaxei limbajului R (IT, JA). Analiza datelor și interpretarea datelor (IT, JA). Discutarea rezultatelor în lumina fundalului teoretic actual (JA, IT). Pregătirea și scrierea articolului (JA, IT). În general, ambii autori au contribuit în mod egal la dezvoltarea acestei lucrări.,
de Finanțare
primul autor dezvăluite primirea următoarele sprijin financiar pentru cercetare, calitatea de autor și/sau publicarea acestui articol: A primit sprijin financiar din partea Chilian Comisia Națională pentru Cercetare Științifică și Tehnologică (CONICYT) „Becas Chile” Doctorat Fellowship program (Grant nr: 72140548).
Declarație privind conflictul de interese
autorii declară că cercetarea a fost efectuată în absența oricăror relații comerciale sau financiare care ar putea fi interpretate ca un potențial conflict de interese.Cronbach, L. (1951)., Coeficientul alfa și structura internă a testelor. Psychometrika 16, 297-334. doi: 10.1007/BF02310555
CrossRef Textul Complet | Google Scholar
McDonald, R. (1999). Teoria testului: un tratament unificat. Lawrence Erlbaum Associates.Google Scholar
echipa de bază de dezvoltare R (2013). R: un limbaj și un mediu pentru calculul statistic. Viena: Fundația R pentru calcul statistic.
Raykov, T. (1997)., Scale reliability, cronbach”s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package „psych.,”Disponibil online la: http://org/r/psych-manual.pdf
Shapiro, A., și ten Berge, J. M. F. (2000). Părtinirea asimptotică a analizei factorului minim de urme, cu aplicații la cea mai mare limită inferioară la fiabilitate. Psychometrika 65, 413-425. doi: 10.1007/BF02296154
CrossRef Textul Complet | Google Scholar
ten Berge, J. M. F., și Sočan, G. (2004). Cea mai mare limită inferioară a fiabilității unui test și a ipotezei unidimensionalității. Psychometrika 69, 613-625. doi: 10.,1007/BF02289858
CrossRef Textul Complet | Google Scholar
Woodhouse, B., și Jackson, P. H. (1977). Limite inferioare pentru fiabilitatea scorului total pe un test compus din elemente neomogene: II: o procedură de căutare pentru a localiza cea mai mare limită inferioară. Psychometrika 42, 579-591. doi: 10.1007/BF02295980
CrossRef Textul Complet | Google Scholar
Apendicele I
R sintaxa pentru a estima coeficienții de fidelitate de la Pearson”s matrici de corelație., Corelația valorilor în afara diagonalei sunt calculate prin înmulțirea factorului de încărcare de elemente: (1) tau-model echivalent acestea sunt toate egale cu 0.3114 (λiλj = 0.558 × 0.558 = 0.3114) și (2) congenere modelul ele pot varia în funcție de diferite factorul de încărcare (de exemplu, matricea element a1, 2 = λ1λ2 = 0.3 × 0.4 = 0.12). În ambele exemple adevărata fiabilitate este 0.731.
> omega(Cr,1)$alfa # standardizate Cronbach”s α
0.731
> omega(Cr,1)$omega.tot # coeficientul ω total
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach”s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731