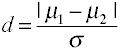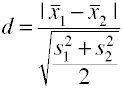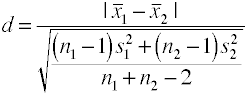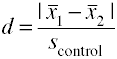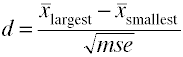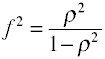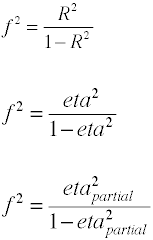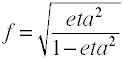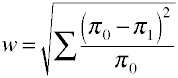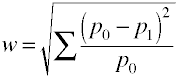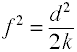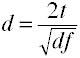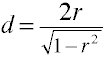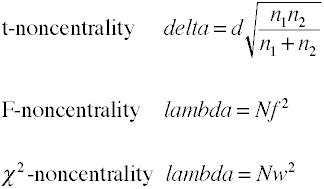o utilizare a dimensiunii efectului este ca un indice standardizat care este independent de mărimea eșantionului și cuantifică magnitudinea diferenței dintre populații sau relația dintre variabilele explicative și de răspuns. O altă utilizare a dimensiunii efectului este utilizarea sa în efectuareaanaliza puterii.
mărimea Efectului pentru diferența în mijloc
mărimea Efectului pentru diferențele în mijloc este dat byCohen e d este definit în termeni de populație mijloace (µs) și o populație standarddeviation (σ), așa cum se arată mai jos.,
Există mai multe moduri diferite în care una ar putea estima σ de date eșantion whichleads mai multe variante în cadrul Cohen ‘ s d familie.
Folosind root mean square abaterea standard
Utilizarea reunite abaterea standard (Hedges’ g)
Această versiune a lui Cohen d utilizează reunite abaterea standard și este, de asemenea, cunoscut sub numele de Garduri vii’ g.,
puteți obține cu ușurință această valoare la o anova program prin luarea rădăcina pătrată a meansquare de eroare, care este, de asemenea, cunoscut sub numele de rădăcina medie pătrată eroare.
folosind deviația standard a grupului de control (sticlă ‘Δ)
o altă versiune a lui Cohen d folosind abaterea standard pentru grupul de control este, de asemenea, cunoscută sub denumirea de sticlă’ Δ.,
Mai mult de două grupuri
atunci Când există mai mult de două grupuri de a folosi diferența dintre cel mai mare și smallestmeans împărțită la rădăcina pătrată din valoarea medie pătrată eroare.
mărimea Efectului pentru F-rate în analiza de regresie
Pentru regresie OLS măsura efectele dimensiunea este F care este definit de către Cohen, după cum urmează.,
din nou, există mai multe moduri în care mărimea efectului poate fi calculat din datele eșantion. Notați că η2 este un alt nume pentru R2.
mărimea Efectului pentru F-rate în analiza de varianță
efectul de mărime utilizată în analiza de varianță este definit de raportul dintre populația standarddeviations.,
Deși Cohen f este definit ca mai sus este, de obicei, computedby având rădăcina pătrată a lui f2.
mărimea Efectului pentru χ2 de tabele de contingență
din nou, începem cu o definiție formula în termeni de populație valori.Dimensiunea efectului w este rădăcina pătrată a statisticii chi-pătrat standardizate.,
Și aici este modul în care w este calculat pe baza eșantionului de date.
Aici este un tabel de valori sugerate de joasă, medie și înaltă efecte (Cohen, 1988). Aceste valori nu ar trebuisă fie luate ca absolute și ar trebui interpretate în contextul programului dvs. de cercetare. Valorile pentruefectele mari sunt frecvent depășite în practică, cu valori D ale lui Cohen mai mari de 1,0, nu mai puțin frecvente.,Cu toate acestea, utilizarea unor dimensiuni de efect foarte mari în analiza potențială a puterii nu este probabil o idee bună, deoarece ar putea duce la studii sub putere.,formule
în cazul în care k = numărul de grupuri
Converti t a d pentru două grupuri independente
Converti r a d pentru două grupuri independente
non-centralității estimările
Analiza de putere folosind metode analitice necesită o estimare non-centralității care este basicallythe mărime a efectului înmulțit cu o mărime a eșantionului factor., Iată câteva formule pentru estimarea neconcentralității.
Exemplu analiza de putere
Aici este un exemplu care aduce împreună mărime a efectului și non-centralității într-o putere de analiză.luați în considerare o analiză unidirecțională a varianței cu trei grupuri (k = 3). Dacă ne așteptăm ca andeta2 să fie egal .,12 în cazul în care mărimea efectului va fi
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
Cu un proiectat eșantion de 60 de estimarea non-centralității este
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
numărătorul de grade de libertate este k-1 = 3-1 = 2, în timp ce numitorul df este N-k = 60-3 = 57.Valoarea critică a lui F cu 2 și 57 de grade de libertate este de 3,16. Ceea ce duce la o putere de
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
astfel, un N de 60 și dimensiunea efectului .369 produce o putere proiectată de aproximativ .7.
putem îmbunătăți pe puterea .7 utilizând o dimensiune proiectată a eșantionului de 75 în loc de 60., Cu aceeași dimensiune a efectului.369, vom obține o nouă estimare noncentrality de
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
gradele numărător de libertate rămân aceleași, în timp ce numitorul df acum Egal N-k = 75-3 = 72.Valoarea critică a lui F cu 2 și 72 de grade de libertate de 3,12. De data aceasta puterea este
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
care se află în limite acceptabile de cercetare.
vă rugăm să rețineți că diferite pachete stat folosesc nume diferite și o ordine diferită de argumente înfuncția pe care o numim noncentralFtail. Va trebui să citiți documentațiavine cu software-ul dvs.,Becker, L. Psihologie 590 note de curs. Vizualizate 19 Jun 2009 <http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen, J. 1988. Analiza statistică a puterii pentru științele comportamentale. Mai multe detalii aici