un Model de regresie pentru datele de supraviețuire
am scris anterior despre cum se calculează curba Kaplan–Meier pentru datele de supraviețuire. Ca estimator non-parametric, face o treabă bună de a da o privire rapidă asupra curbei de supraviețuire pentru un set de date. Cu toate acestea, ceea ce nu vă permite să faceți este să modelați impactul covariatelor asupra supraviețuirii. În acest articol, ne vom concentra pe modelul Cox proporțional Hazards, unul dintre cele mai utilizate modele pentru datele de supraviețuire.
vom intra în profunzime cu privire la modul de calculare a estimărilor., Acest lucru este valoros, deoarece vom vedea că estimările depind doar de ordonarea eșecurilor și nu de timpul lor real. De asemenea, vom discuta pe scurt câteva probleme dificile despre inferența cauzală care sunt speciale pentru analiza supraviețuirii.de obicei, ne gândim la datele de supraviețuire în ceea ce privește curbele de supraviețuire precum cea de mai jos.,
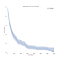
Pe axa x, avem timp în zile. Pe axa y, avem (un estimator pentru) procentul (din punct de vedere tehnic, proporția) subiecților din populație care „supraviețuiesc” până la acel moment. Supraviețuirea poate fi figurativă sau literală., Ar putea fi dacă oamenii trăiesc la o anumită vârstă, dacă o mașină face o anumită perioadă de timp, fără a rupe în jos, sau ar putea fi dacă cineva rămâne șomer o anumită perioadă de timp după ce și-a pierdut locul de muncă.în mod crucial, complicația în analiza supraviețuirii este că unii subiecți nu au” moartea ” lor observată. S-ar putea să fie încă în viață, o mașină ar putea funcționa în continuare sau cineva ar putea fi încă șomer la momentul colectării datelor., Astfel de observații sunt numite „corect cenzurate” și care se ocupă cu cenzura înseamnă că analiza de supraviețuire necesită diferite instrumente statistice.
noi denumim funcția supraviețuitor ca S, o funcție de timp. Producția sa este procentul de subiecți care au supraviețuit la momentul t. (din nou, este punct de vedere tehnic o proporție între 0 și 1, dar voi folosi cele două cuvinte alternativ). Pentru simplitate vom face presupunerea tehnică că, dacă așteptăm suficient de mult, toți subiecții vor ” muri.”
vom indexa subiecții cu un indice ca i sau j., Eșecul ori de întreaga populație va fi indicat cu același indice la variabila timp t.

O altă subtilitate să ia în considerare este dacă tratăm timp cât mai discret (săptămână de săptămână, să zicem) sau continuu. Din punct de vedere filosofic, măsurăm doar timpul în trepte discrete (până la cea mai apropiată secundă, să zicem)., În mod obișnuit, datele noastre ne vor spune doar dacă cineva a murit într-un anumit an sau dacă o mașină a eșuat într-o anumită zi. Voi merge înainte și înapoi între cazurile discrete și continue, în scopul de a menține expunerea cât mai clară posibil.când încercăm să modelăm efectele covariatelor (de exemplu, vârstă, sex, rasă, producător de mașini), vom fi de obicei interesați să înțelegem efectul covariatului asupra ratei de pericol. Rata de pericol este probabilitatea instantanee de eșec/deces / tranziție de stat la un moment dat t, condiționată de supraviețuirea deja atât de lungă., Vom indica λ (t). Tratarea timp, cât mai discret:
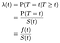
Unde f este în general densitatea de probabilitate de faptul că nu la momentul t. Putem unifica discrete și continue cazuri, permițându-delta funcțiile densitate de probabilitate „funcție”. Astfel, rezultatul λ = f / S este același pentru cazul continuu.
să fixăm un exemplu., Să luăm în considerare contextul unui studiu clinic în care un medicament determină inițial o boală să intre în remisie. Vom spune că medicamentul „nu reușește” pentru un subiect atunci când boala începe să progreseze pentru un subiect. În cele din urmă, să presupunem că starea bolii subiecților este măsurată în fiecare săptămână. Apoi, Dacă λ ( 3) = 0, 1, înseamnă că există o șansă de 10% ca, pentru un anumit subiect, dacă sunt încă în remisie înainte de săptămâna 3, boala lor va începe să progreseze în săptămâna 3. Celelalte 90% vor rămâne în remisie.,
în continuare, funcția generală de densitate de probabilitate f este doar derivata lui S în ceea ce privește timpul. (Din nou, dacă timpul este discret, f este doar suma unor funcții delta).,341fa8b2″>
Acest lucru înseamnă că, dacă știm Pericol funcție, putem rezolva această ecuație diferențială pentru S:
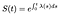
Dacă timpul este discret, integrala de o sumă de delta funcții doar se transformă într-o sumă de pericole la fiecare timp discret.,
bine, asta rezumă notația și conceptele de bază de care vom avea nevoie. Să trecem la discutarea modelelor.
modele Non-, Semi-și complet parametrice
așa cum am spus mai devreme, suntem de obicei interesați să modelăm rata de pericol λ.într-un model non-parametric, nu facem presupuneri despre forma funcțională a λ. Curba Kaplan-Meier este Estimatorul probabilității maxime în acest caz. Dezavantajul este că acest lucru face dificilă modelarea oricăror efecte ale covariatelor. Este un pic ca folosind un complot scatter pentru a înțelege efectul unui covariat., Nu este neapărat la fel de util ca un model complet parametric ca o regresie liniară.într-un model complet parametric, facem o presupunere pentru forma funcțională precisă a λ. O discuție a modelelor complet parametrice este un articol complet în sine, dar merită o discuție foarte scurtă. Tabelul de mai jos prezintă trei dintre cele mai comune modele complet parametrice. Fiecare este generalizat de următorul, mergând de la 1 la 2 la 3 parametri. Forma funcțională pentru funcția de pericol este prezentată în coloana din mijloc. Logaritmul funcției de pericol este prezentat și în ultima coloană., Se presupune că toți parametrii (ɣ, α, μ) sunt pozitivi, cu excepția faptului că μ ar putea fi 0 în distribuția generalizată Weibull (reproducând distribuția Weibull).

Se uită la logaritmul ne arată că modelul exponențial presupune că pericolul funcția este constantă. Modelul Weibull presupune că crește dacă α>1, constantă Dacă α=1 și descrescătoare Dacă α< 1., Modelul Weibull generalizat începe la fel ca modelul Weibull (la început ln s = 0). După aceea, un termen suplimentar μ intră.
problema cu aceste modele este că fac presupuneri puternice despre date. În anumite contexte, pot exista motive să credem că aceste modele sunt potrivite. Dar, cu aceste și alte câteva opțiuni disponibile, există un risc puternic de a trage concluzii incorecte din cauza specificării greșite a modelului.acesta este motivul pentru care riscurile proporționale Cox, un model semi-parametric este atât de popular., Nu se fac ipoteze funcționale cu privire la forma funcției de pericol; în schimb, se fac ipoteze funcționale cu privire la efectele covariatelor singure.,
Cox Proporțională a riscurilor Model
Cox Proporțională a riscurilor Model este dat, de obicei, în termeni de timp t, covariate vector x, și coeficientul de vectorul β
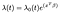
unde λₒ este o funcție arbitrară de timp, pe bază de pericol. Produsul punct al X și β este luat în exponent la fel ca în regresia liniară standard., Indiferent de valorile covariabile, toți subiecții au același risc inițial λₒ. Ulterior, ajustările se fac pe baza covariatelor.
Interpretarea Rezultatelor
să Presupunem pentru o clipă că ne-am potrivi un Cox Proporțională a riscurilor modelul datelor noastre, care a constat din
- O coloană specificarea timp pentru fiecare subiect
- O coloană în care se precizează dacă subiectul a fost „observat” (a nu au reușit, sau, în nostru preferat exemplu, pentru a avea boala lor de progres). O valoare de 1 înseamnă că subiectul a avut progresul bolii., O valoare de 0 înseamnă că, la ultimul timp de observație, boala nu a progresat. Observația a fost cenzurată.
- coloane pentru covariatele noastre X.
după potrivire, vom obține valori pentru β. De exemplu, să presupunem pentru simplitate că există un singur covariat. O valoare de β=0,1 înseamnă că o creștere a covariatului cu o cantitate de 1 conduce la o șansă mare de aproximativ 10% de progresie a bolii la un moment dat., Valoarea exactă este, de fapt,

Pentru valori mici ale lui β, valoarea lui β în sine este o foarte bună aproximare exactă a crește în pericol. Pentru valori mai mari ale β, trebuie calculată suma exactă.un alt mod de a exprima β = 0, 1 este că, pe măsură ce x crește, pericolul crește cu o rată de 10% pe creșterea x cu 1. Mai mare 10.,52% provine din compoundarea (continuă), la fel ca în cazul dobânzii compuse.
de asemenea, β=0 nu înseamnă niciun efect, iar β negativ înseamnă că există un risc mai mic pe măsură ce crește covariatul. Rețineți că, spre deosebire de regresiile standard, nu există un termen de interceptare. În schimb, interceptarea este absorbită în pericolul de bază λₒ, care poate fi, de asemenea, estimat (vezi mai jos).în cele din urmă, presupunând că am estimat funcția de pericol de bază, putem construi funcția supraviețuitor.,
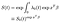
funcția de bază este ridicat la puterea a exp(xʹß) factor de covariabile. Trebuie acordată o atenție deosebită interpretării funcției supraviețuitorului de bază, care joacă aproximativ rolul termenului de interceptare într-o regresie liniară regulată. Dacă covariatele au fost centrate (media 0), atunci reprezintă funcția de supraviețuitor pentru subiectul „mediu”.,
Estimarea Cox Proporțională a riscurilor Model
În 1970, David Cox, un matematician Britanic, a propus o modalitate de a estima β fără a fi nevoie să estimeze valoarea inițială de pericol λₒ. Din nou, riscul inițial poate fi estimat ulterior. Așa cum am menționat mai devreme, vom vedea că este ordonarea eșecurilor observate care contează, nu vremurile în sine.înainte de a sări în estimare, merită să discutăm legăturile. Deoarece de obicei observăm datele doar în incremente discrete, este posibil ca două eșecuri să apară în același timp., De exemplu, două mașini ar putea eșua în aceeași săptămână, iar înregistrarea se face doar săptămânal. Aceste legături fac ca analiza situației să fie destul de complicată, fără a adăuga multă înțelegere. În consecință, voi deduce estimările în cazul în care nu există legături.reamintim că datele noastre constau în observații ale unor eșecuri de număr la un moment discret. Fie R (t) să denotă populația „la risc” la momentul t. dacă un subiect din studiul nostru a eșuat (boala a progresat, de exemplu) înainte de ora t, ei nu sunt „în pericol.,”De asemenea, dacă un subiect din studiul nostru și-a cenzurat observația la un moment dat înainte de ora t, ei nu sunt, de asemenea, „în pericol.”
în mod obișnuit, vrem să construim o funcție de probabilitate (care este probabilitatea că am fi observat datele pe care le-am făcut, având în vedere covariatele și coeficienții) și apoi să optimizăm asta pentru a obține un estimator de probabilitate maximă.
pentru fiecare moment discret când am observat un eșec al subiectului j, probabilitatea ca acesta să apară, având în vedere că a apărut un eșec, este mai jos. Suma este preluată de toți subiecții cu risc la momentul j.,

Observați că linia de bază de pericol λₒ a renuntat! Foarte convenabil. Din acest motiv, probabilitatea pe care o construim este doar o probabilitate parțială. Observați, de asemenea, că vremurile nu apar deloc., Termenul pentru subiectul j depinde numai de subiecții care sunt încă în viață la momentul j, care la rândul lor depinde numai de ordinea în care subiecții sunt cenzurați sau observați că nu reușesc.probabilitatea parțială este, desigur, doar produsul acestor Termeni, unul pentru fiecare eșec pe care îl observăm (fără termeni pentru observații cenzurate).,
jurnal parțială probabilitatea este apoi
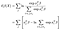
se potrivesc este făcut cu standard de metode numerice, de exemplu, în pachetul python statsmodels și matricea de varianță-covarianță pentru estimări este dat de (inversul) Fisher Informații Matrice. Nimic interesant aici.,
estimarea funcției de bază a supraviețuitorului
acum că am estimat coeficienții, putem estima funcția supraviețuitorului. Acest lucru sfârșește prin a fi foarte similar cu estimarea unei curbe Kaplan-Meier.
postulăm termenii α indexați de i.la momentul i, curba supraviețuitorului inițial ar trebui să scadă cu o fracție α reprezentând proporția subiecților cu risc care nu reușesc la momentul I., Cu alte cuvinte
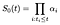
Pentru a calcula probabilitatea maximă estimator pentru α, considerăm probabilitatea contribuția la subiectul i, care nu reușește la timp m-am și separat contribuția la cei care sunt cenzurate la momentul i.
Pentru un subiect care nu reușește la timp, am, de probabilitate este dată de probabilitatea ca acestea sunt în viață la momentul i mai puțin probabilitatea ei sunt în viață la data viitoare i+1. (Presupunem temporar că orele sunt ordonate).,
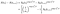
Dacă în schimb, ei sunt cenzurate la momentul i, contribuția este doar probabilitatea ei sunt în viață la momentul după ce eu, și anume că ei nu au murit încă., Aceasta este doar
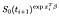
Nu este un termen suplimentar de subiecți care au fost observate (de exemplu, observat pentru a reuși în loc de cenzurat)., Jurnalul probabilitatea devine
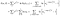
am fost un pic neglijent cu privire la urmărirea de obiective (i vs i+1), dar se va rezolva totul.
există doar Termeni α pentru subiecții pe care i-am observat că nu reușesc., Diferențiind în ceea ce privește α-j și presupunând că nu există legături, obținem o contribuție din suma din stânga numai pentru subiecții în viață la momentul j și o singură contribuție din termenul din dreapta.,qual la 0 înseamnă că putem obține estimări de probabilitate maximă pentru α folosind estimările noastre pentru β ca soluție la mai multe ecuații, una pentru fiecare subiect, care a fost observat pentru a reuși:
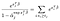
Extensii și Limitări
Există o mulțime mai multe de spus despre Cox Proporțională a riscurilor modele, dar voi încerca să păstreze lucrurile scurtă și menționa doar câteva lucruri.,de exemplu, este posibil să doriți să luați în considerare regresorii care variază în timp, iar acest lucru este posibil.un alt lucru crucial pentru a păstra în minte este omisă părtinire variabilă. În regresia liniară standard, variabilele omise necorelate cu regresorii nu sunt o mare problemă. Acest lucru nu este adevărat în analiza supraviețuirii. Să presupunem că avem două sub-populații de dimensiuni egale și eșantionate în datele noastre, fiecare cu o rată de pericol constantă, una este 0.1, iar cealaltă este 0.5. Inițial, vom vedea o rată mare de pericol (media, doar 0,3)., Odată cu trecerea timpului, populația cu o rată de pericol ridicată va părăsi populația și vom observa o rată de pericol care scade spre 0.1. Dacă am omis variabila reprezentând aceste două populații, rata noastră de risc de bază va fi dat peste cap.