8.1 Un exemplu istoric
În cartea sa, Cele Două Noi Științe, Galileo Galilea (1564-1642), oferă mai multe argumente pentru a demonstra că nu poate exista un astfel de lucru ca infinități actuale sau reale infinitesimals. Unul dintre argumentele sale poate fi reconstruit în felul următor. Galileo propune să luăm ca premisă faptul că există o infinitate reală de numere naturale (numerele naturale sunt numerele întregi pozitive de la 1):
{1, 2, 3, 4, 5, 6, 7, ….,}
el propune, de asemenea, să luăm ca premisă că există o infinitate reală a pătratelor numerelor naturale.
{1, 4, 9, 16, 25, 36, 49, ….}
acum, Galileo motive, rețineți că aceste două grupuri (astăzi le-am numi „seturi”) au aceeași dimensiune. Putem vedea acest lucru pentru că putem vedea că există o corespondență unu-la-unu între cele două grupuri.,
| {1, | 2, | 3, | 4, | 5, | 6, | 7, ….,div> | |
| {1, | 4, | 9, | 16, | 25, | 36, | 49, …} |
Dacă putem asocia fiecare număr natural cu unul și numai un singur număr de pătrate, și dacă putem asocia fiecare număr pătrat cu unul și numai un singur număr natural, atunci aceste seturi trebuie să fie de aceeași dimensiune.,
dar așteptați un moment, spune Galileo. Există, evident, foarte multe numere mai naturale decât există numere pătrate. Adică, fiecare număr pătrat se află în lista numerelor naturale, dar multe dintre numerele naturale nu se află în lista numerelor pătrate. Următoarele numere sunt toate în lista de numere naturale, dar nu în lista de numere pătrate.
{2, 3, 5, 6, 7, 8, 10, ….,}
deci, Galileo motive, în cazul în care există mai multe numere în grupul de numere naturale care nu sunt în grupul de numere pătrate, și dacă nu există numere în grupul de numere pătrate care nu sunt în numerele naturals, atunci numerele naturale este mai mare decât numerele pătrate. Și dacă grupul numerelor naturale este mai mare decât grupul numerelor pătrate, atunci numerele naturale și numerele pătrate nu au aceeași dimensiune.,
am ajuns la două concluzii: setul de numere naturale și setul de numere pătrate sunt de aceeași dimensiune; și, setul de numere naturale și setul de numere pătrate nu sunt de aceeași dimensiune. E contradictoriu.Galileo susține că motivul pentru care am ajuns la o contradicție este că am presupus că există infinități reale. Prin urmare, el concluzionează că nu există infinități reale.
8.2 dovezi indirecte
logica noastră nu este încă suficient de puternică pentru a dovedi unele argumente valide. Luați în considerare următorul argument ca exemplu.,
(P→(QvR))
Q
R
P
Acest argument pare valabil. Prin prima premisă știm: dacă P au fost adevărate, atunci așa ar fi (Q v R) fi adevărat. Dar atunci fie Q, fie R, fie ambele ar fi adevărate. Și prin a doua și a treia premisă știm: Q este fals și R este fals. Deci nu poate fi că (Q v R) este adevărat, și deci nu poate fi că P este adevărat.
putem verifica argumentul folosind un tabel de adevăr. Masa noastră va fi complexă, deoarece una dintre premisele noastre este complexă.,
In any kind of situation in which all the premises are true, the conclusion is true., Adică: premisele sunt adevărate numai în ultimul rând. Pentru acel rând, concluzia este, de asemenea, adevărată. Deci, acesta este un argument valid.dar să ia un minut și să încerce să dovedească acest argument. Începem cu

și acum suntem opriți. Nu putem aplica niciuna dintre regulile noastre. Iată un argument valid pe care nu l-am făcut sistemul nostru de raționament suficient de puternic pentru a dovedi.există mai multe modalități de a remedia această problemă și de a face sistemul nostru de raționament suficient de puternic., Una dintre cele mai vechi soluții este introducerea unei noi metode de dovadă, numită în mod tradițional „reductio ad absurdum”, ceea ce înseamnă o reducere la absurditate. Această metodă este adesea numită „dovadă indirectă”sau” derivare indirectă”.ideea este că presupunem negarea concluziei noastre și apoi arătăm că rezultă o contradicție. O contradicție este arătată atunci când dovedim o propoziție Ψ și negarea ei Ψ. Aceasta poate fi orice propoziție. Ideea este că, având în vedere principiul bivalenței, trebuie să fi dovedit ceva fals. Căci dacă Ψ este adevărat, atunci Ψ este fals; și Dacă Ψ este adevărat, atunci Ψ este fals., Nu trebuie să știm care este fals (Ψ sau Ψ); este suficient să știm că unul dintre ei trebuie să fie.amintiți-vă că ne-am construit sistemul logic astfel încât să nu poată produce o minciună din declarații adevărate. Sursa falsității pe care o producem în derivarea indirectă trebuie, prin urmare, să fie o minciună pe care am adăugat-o argumentului nostru. Și ceea ce am adăugat la argumentul nostru este negarea concluziei. Astfel, concluzia trebuie să fie adevărată.,
forma de argument este ca aceasta:

în mod Tradițional, ipoteza indirecte de derivare a fost, de asemenea, numit de obicei „adormirea maicii domnului pentru reductio”.
ca exemplu concret, putem dovedi cazul nostru nedumerit.

Am presupus negarea concluzia noastră pe linia 4. Concluzia pe care am crezut-o a fost corectă a fost P, iar negarea acestui lucru este P. în linia 7, am dovedit R., Tehnic, am terminat în acel moment, dar am dori să fim amabili cu oricine încearcă să înțeleagă dovada noastră, așa că repetăm linia 3, astfel încât propozițiile R și R să fie una lângă alta și este foarte ușor să vedem că ceva nu a mers bine. Adică, dacă am dovedit atât R, cât și R, atunci am dovedit ceva fals.
raționamentul nostru merge acum așa. Ce a mers prost? Linia 8 este o utilizare corectă a repetiției; linia 7 provine dintr-o utilizare corectă a Modus tollendo ponens; linia 6 dintr-o utilizare corectă a Modus ponens; linia 5 dintr-o utilizare corectă a negării duble., Deci, nu am făcut o greșeală în raționamentul nostru. Am folosit liniile 1, 2 și 3, dar acestea sunt premisele pe care am fost de acord să presupunem că sunt corecte. Aceasta lasă linia 4. Asta trebuie să fie sursa contradicției mele. Trebuie să fie fals. Dacă linia 4 este falsă, atunci P este adevărat.unii oameni consideră dovezile indirecte mai puțin puternice decât dovezile directe. Există multe și complexe motive pentru acest lucru. Dar, pentru logica noastră propozițională, niciunul dintre aceste motive nu se aplică. Acest lucru se datorează faptului că este posibil să dovedim că logica noastră propozițională este consecventă., Aceasta înseamnă că este posibil să dovedim că logica noastră propozițională nu poate dovedi o minciună decât dacă cineva introduce mai întâi o minciună în sistem. (În general, nu este posibil să se demonstreze că sistemele logice sau matematice mai puternice și avansate sunt consecvente, din interiorul acestor sisteme; de exemplu, nu se poate dovedi în aritmetică că aritmetica este consecventă.) Având în vedere că putem fi siguri de coerența logicii propoziționale, putem fi siguri că în logica propozițională o dovadă indirectă este o formă bună de raționament., Știm că dacă dovedim o minciună, trebuie să fi pus o minciună; și dacă suntem încrezători în toate celelalte ipoteze (adică premisele) dovezii noastre, cu excepția presupunerii pentru derivarea indirectă, atunci putem fi siguri că această presupunere pentru derivarea indirectă trebuie să fie sursa falsității.o notă despre terminologie este necesară aici. Cuvântul „contradicție” este folosit ambiguu în majoritatea discuțiilor logice. Poate însemna o situație așa cum vedem mai sus, în care se afirmă două propoziții, iar aceste propoziții nu pot fi adevărate., Sau poate însemna o singură propoziție care nu poate fi adevărată. Un exemplu de astfel de propoziție este (P^P)., Tabelul de adevăr pentru această teză este:
| P | P | (P ^ P) |
|---|---|---|
| T | F | F |
| F | T | F |
Astfel, acest tip de propoziție nu poate fi adevărată, indiferent de sensul de P.,pentru a evita ambiguitatea, în acest text, vom numi întotdeauna o singură propoziție care nu poate fi adevărată o „propoziție contradictorie”. Astfel, (P^P) este o propoziție contradictorie. Situațiile în care se afirmă două propoziții care nu pot fi adevărate vor fi numite „contradicție”.
8.3 exemplul nostru și alte exemple
putem reconstrui acum o versiune a argumentului lui Galileo. Vom folosi următoarea cheie.P: există infinități reale (inclusiv numerele naturale și numerele pătrate).,Q: există o corespondență unu-la-unu între numerele naturale și numerele pătrate.
R: dimensiunea setului de numere naturale și dimensiunea setului de numere pătrate sunt aceleași.
S: toate numerele pătrate sunt numere naturale.
T: unele dintre numerele naturale nu sunt numere pătrate.
U: există mai multe numere naturale decât numere pătrate.,
Cu această cheie, argumentul va fi tradus:
(P→Q)
(Q→R)
(P→(S^T))
((S^T)→U)
(U→R)
P
Și putem demonstra acest lucru este un argument valid prin utilizarea indirectă derivare:

Pe linia 6, ne-am asumat-P pentru că Galileo a crezut că P și menite să demonstreze că P. Care este, el crede că nu sunt reale infinituri, și așa a crezut că este fals să credem că nu este cazul că nu sunt reale infinituri. Această falsitate va duce la alte falsuri, expunându-se.,pentru cei interesați: Galileo a concluzionat că nu există infinități reale, dar există infinități potențiale. Astfel, el a motivat, nu este cazul ca toate numerele naturale să existe (într-un anumit sens de „există”), dar este adevărat că puteți număra numerele naturale pentru totdeauna. Mulți filozofi înainte și după Galileo au susținut această viziune; este similar cu o viziune a lui Aristotel, care a fost un logician și filozof important care a scris cu aproape două mii de ani înainte de Galileo.,rețineți că într-un argument ca acesta, ați putea argumenta că nu presupunerea pentru derivarea indirectă, ci mai degrabă una dintre premise a fost sursa contradicției. Astăzi, majoritatea matematicienilor cred acest lucru despre argumentul lui Galileo. Un logician și matematician pe nume Georg Cantor (1845-1918), inventatorul teoriei seturilor, a susținut că seturile infinite pot avea subseturi adecvate de aceeași dimensiune., Adică, Cantor a negat premisa 4 de mai sus: chiar dacă toate numerele pătrate sunt numere naturale și nu toate numerele naturale sunt numere pătrate, nu este cazul ca aceste două seturi să aibă dimensiuni diferite. Cantor a acceptat totuși premisa 2 de mai sus și, prin urmare, a crezut că dimensiunea setului de numere naturale și dimensiunea setului de numere pătrate este aceeași. Astăzi, folosind raționamentul lui Cantor, matematicienii și logicienii studiază infinitul și au dezvoltat un mare număr de cunoștințe despre natura Infinitului. Dacă acest lucru vă interesează, consultați secțiunea 17.5.,să luăm în considerare un alt exemplu pentru a ilustra derivarea indirectă. Un set foarte util de teoreme sunt astăzi numite „teoremele lui De Morgan”, după logicianul Augustus De Morgan (1806-1871). Nu putem afirma aceste integral până capitolul 9, dar putem statului echivalentul lor în limba engleză: DeMorgan a observat că (PvQ) si (P^Q) sunt echivalente, și, de asemenea, că (P^Q) și (PvQ) sunt echivalente. Având în vedere acest lucru, ar trebui să fie o teoremă a limbii noastre care ((PvQ)→(P^Q)). Să dovedim asta.
întreaga formulă este condiționată, deci vom folosi o derivare condiționată., Dovada noastră trebuie să înceapă astfel:
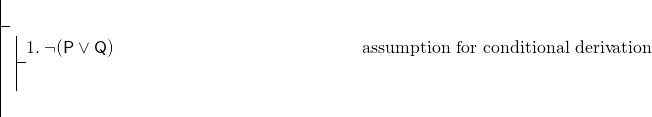
pentru a finaliza derivarea condiționată, trebuie să dovedim (P^Q). Aceasta este o conjuncție, Iar regula noastră pentru a arăta conjuncții este adjuvanța. Din moment ce folosind această regulă ar putea fi cel mai bun mod nostru de a arăta (P^Q), putem urmări pentru a arăta P și apoi arată Q, și apoi efectua adjunction. Dar, evident, avem foarte puțin pentru a lucra cu—doar linia 1, Care este o negare. Într-un astfel de caz, este de obicei înțelept să încerce o dovadă indirectă. Începeți cu o dovadă indirectă a lui P.,

acum trebuie să găsim o contradicție—orice contradicție. Dar există deja unul evident. Linia 1 spune că nici P, nici Q nu este adevărat. Dar linia 3 spune că P este adevărat. Trebuie să explicăm această contradicție găsind o formulă și negarea ei. Putem face acest lucru folosind adăugarea.

Pentru a finaliza dovada, vom folosi această strategie din nou.

Vom dovedi De Morgan teoreme și probleme pentru capitolul 9.,
Iată o regulă generală de bază pentru a face dovezi: atunci când dovediți o condiționalitate, faceți întotdeauna derivarea condiționată; în caz contrar, încercați derivarea directă; dacă aceasta nu reușește, atunci încercați derivarea indirectă.
8.4 probleme
- completați următoarele dovezi. Fiecare va necesita o derivare indirectă. Ultimele două sunt provocatoare.
- dovediți că următoarele sunt teoreme.
- (p^P).
- ((p→p)^(p→p)).
- (P→(P^Q)).
- ((p^Q)→(p→Q)).
- În engleză colocvială normală, scrieți propriul argument valid cu cel puțin două premise., Argumentul dvs. ar trebui să fie doar un paragraf (nu o listă ordonată de propoziții sau orice altceva care arată ca o logică formală). Traduceți-l în logică propozițională și dovediți că este valabil folosind o derivare indirectă.această traducere a titlului cărții lui Galileo a devenit cea mai comună, deși una mai literală ar fi fost discursurile și demonstrațiile matematice. Traducerile cărții includ Drake (1974).