
Pitagora
Peste 2000 de ani în urmă, acolo a fost o descoperire uimitoare despre triunghiuri:
atunci Când un triunghi are un unghi drept (90°) …
… și pătratele sunt făcute pe fiecare dintre eletrei laturi, …
… apoi, cel mai mare pătrat are exact aceeași zonă ca și celelalte două pătrate puse împreună!,
Acesta este numit „Pitagora” Teorema” și poate fi scris într-o scurtă formulă:
a2 + b2 = c2
Notă:
- c este cea mai lungă latură a triunghiului
- a și b sunt alte două părți
Definitie
Cea mai lungă latură a triunghiului este numit „ipotenuza”, astfel încât definiția formală este:
Într-un triunghi dreptunghic:
pătratul ipotenuzei este egal cu
suma pătratelor celorlalte două laturi.,
sigur … ?
Să vedem dacă funcționează cu adevărat folosind un exemplu.

de ce este util acest lucru?dacă cunoaștem lungimile a două laturi ale unui triunghi unghi drept, putem găsi lungimea celei de-a treia laturi. (Dar amintiți-vă că funcționează doar pe triunghiuri în unghi drept!)
cum îl folosesc?,
Scrie ca o ecuație:
 |
a2 + b2 = c2 |
Apoi vom folosi algebra pentru a găsi orice lipsă de valoare, ca în aceste exemple:
de asemenea, puteți citi despre Piețe și Rădăcini Pătrate pentru a afla de ce √169 = 13
functioneaza invers, prea: atunci când cele trei laturi ale unui triunghi fac a2 + b2 = c2, atunci triunghiul este dreptunghic.,
și puteți dovedi singur Teorema !
Obțineți stilou de hârtie și foarfece, apoi utilizați următoarea animație ca ghid:
- desenați un triunghi în unghi drept pe hârtie, lăsând mult spațiu.,
- a Desena un pătrat de-a lungul ipotenuzei (partea cea mai lunga)
- Trage aceleași dimensiuni pătrat pe de altă parte ipotenuzei
- a Desena linii cum se arată în animație, astfel:

- Taie forme
- Aranjați-le astfel încât să puteți dovedi că piața mare are aceeași zonă ca și cele două pătrate de pe alte părți
un Alt, Uimitor de Simplu, Dovada
Aici este una dintre cele mai vechi dovezi că piața pe latura lungă a aceeași zonă ca și alte piețe., urmăriți animația și acordați atenție atunci când triunghiurile încep să alunece. poate doriți să vizionați animația de câteva ori pentru a înțelege ce se întâmplă.
triunghiul violet este cel important.
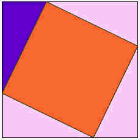 |
devine | 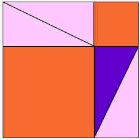 |

