„eu, în orice caz, sunt convins că El nu se arunca zarurile.,”
~ Albert Einstein
- Variabile Aleatoare
- Discrete Variabile Aleatoare
- Continuu Variabile Aleatoare
- Amestecat Variabile Aleatoare
- Cumulativ Funcțiile de Distribuție (CDF)
- Funcția Densității de Probabilitate (PDF)
- Interactive CDF/PDF Exemplu
Variabile Aleatoare:

să Zicem că ia o monedă din buzunar și aruncă-l în aer. În timp ce se răstoarnă prin spațiu, ce ai putea spune despre viitorul său?
va ateriza capul în sus? Pajură?, Mai mult decât atât, cât timp va rămâne în aer? De câte ori va sări? Cât de departe de locul în care va atinge primul pământ va ajunge în cele din urmă să se odihnească? De fapt, va lovi vreodată pământul? Ai venit vreodată să te odihnești?pentru unele astfel de întrebări, putem și ne putem baza pe răspunsuri cu mult înainte de observații; suntem destul de siguri că gravitația va ține și moneda va ateriza. Dar pentru alții nu avem de ales decât să judecăm și să vorbim în termeni mai vagi, dacă dorim să spunem ceva util despre viitor.,ca oameni de știință, este, desigur, treaba noastră să spunem ceva util (sau cel puțin autoritar…), în timp ce monedele metaforice ale sistemului fizic important sunt încă în aer. Cap sau Pajură poate fi chiar o chestiune de viață sau de moarte. Monedele noastre pot fi, de exemplu, diverse debite posibile de răcire sau mase de uraniu într-o centrală nucleară. Ne pasă foarte mult să știm care sunt șansele noastre că vom obține turbine zbârnâit în loc de un colaps.,
pentru un determinist strict, toate aceste pariuri au fost decontate cu mult înainte ca orice monedă, metaforică sau nu, să fie bătută vreodată; pur și simplu nu o știm încă. Dacă am ști doar forțele aplicate la aruncarea unei monede, distribuția exactă a masei, diferitele mișcări minuscule ale aerului din cameră… Dacă am ști toate acestea, atunci am ști că aruncarea monedelor a avut o șansă de 100% de a ateriza așa cum va ateriza și șanse zero de orice alt rezultat. dar, desigur, ne lipsește adesea chiar și o fracțiune menționabilă a unei astfel de cunoașteri a lumii., În plus, se pare că în extrem de solzi mici, care stricte determinists sunt absolut greșit; nu există nici o modalitate de a prezice când, de exemplu, un atom de uraniu se va împărți, și dacă un astfel de eveniment afectează mai mare lumea asta macro eveniment este cu adevărat imprevizibile. Unele rezultate sunt cu adevărat în aer, neliniștite până când fac parte din trecut. pentru a face față acestei realități și pentru a putea descrie stările viitoare ale unui sistem într-un mod util, folosim variabile aleatorii., O variabilă aleatoare este pur și simplu o funcție care se referă fiecare rezultat fizic posibil al unui sistem la un număr unic, real. Ca atare, există trei tipuri de variabile aleatorii: discrete, continue și mixte. În secțiunile următoare, aceste categorii vor fi discutate pe scurt și vor fi prezentate exemple.
variabile aleatoare Discrete:
luați în considerare din nou moneda noastră. Am putea avea cap sau Pajură ca rezultate posibile. Dacă am defini o variabilă, x, ca număr de capete într-o singură aruncare, atunci x ar putea fi 1 sau 0, nimic altceva., O astfel de funcție, x, ar fi un exemplu de variabilă aleatorie discretă. Astfel de variabile aleatorii pot lua doar valori discrete. Alte exemple ar fi rezultatele posibile ale unui test de sarcină sau numărul de elevi dintr-o sală de clasă.
variabile aleatoare continue:
înapoi la aruncarea monedei, dacă am dori să descriem distanța dintre locul în care moneda noastră a ajuns să se odihnească și locul în care a lovit prima dată pământul. Această distanță, x, ar fi o variabilă aleatoare continuă, deoarece ar putea prelua un număr infinit de valori în intervalul continuu de numere reale., Moneda ar putea călători 1 cm, sau 1,1 cm, sau 1,11 cm, sau pe și de pe. Alte exemple de variabile aleatorii continue ar fi masa stelelor din galaxia noastră, pH-ul apelor oceanice sau timpul de rezidență al unor analiți într-un cromatograf de gaze.
variabile aleatoare mixte:
variabilele aleatoare mixte au atât componente discrete, cât și continue. Astfel de variabile aleatorii sunt rareori întâlnite. Pentru un exemplu posibil, totuși, este posibil să măsurați greutatea unui eșantion și să decideți că orice greutate măsurată ca valoare negativă va primi o valoare de 0., În acest fel, variabila aleatorie are o Componentă discretă la x = 0 și o componentă continuă unde x > 0.
funcții de distribuție Cumulative (CDF):
întrebarea, desigur, apare cu privire la modul de a descrie cel mai bine matematic (și afișa vizual) variabile aleatoare. Pentru aceste sarcini folosim funcții de densitate de probabilitate (PDF) și funcții de densitate cumulativă (CDF). Deoarece CDF-urile sunt mai simple de înțeles atât pentru variabilele aleatorii discrete, cât și pentru cele continue decât PDF-urile, vom explica mai întâi CDF-urile.luați în considerare aruncarea unui zar echitabil cu 6 laturi., Am avea o șansă de 1 în 6 de a obține oricare dintre valorile posibile ale variabilei aleatoare(1, 2, 3, 4, 5, sau 6). Dacă trasăm acele valori posibile pe axa x și trasăm probabilitatea de a măsura fiecare valoare specifică, x sau orice valoare mai mică decât x pe axa y, vom avea CDF a variabilei aleatoare.
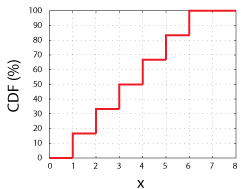
CDF pentru un Târg 6-Sidded Zaruri. Rețineți că fiecare pas este o înălțime de 16,67%, sau 1 din 6.
această funcție, CDF (x), ne spune pur și simplu cotele de măsurare a oricărei valori până la și inclusiv x., Ca atare, toate CDF-urile trebuie să aibă toate aceste caracteristici:
- un CDF trebuie să fie egal cu 0 când x = – ∞ și abordarea 1 (sau 100%) când x se apropie de +∞. Mai simplu spus, din toate rezultatele posibile, trebuie să existe un rezultat; șansa de a arunca un zar cu șase fețe și de a obține o valoare între -∞ și ∞ este de 100%.
- panta unui CDF trebuie să fie întotdeauna egală sau mai mare decât zero. De exemplu, luați în considerare șansa de a arunca un zar cu 6 laturi (corect sau nu) și de a obține o valoare între 0 și 4., Această șansă nu poate fi mai mult decât șansa de a obține o valoare între 0 și 5, deoarece șansele unei aterizări 1, 2 sau 3 cu fața în sus vor fi, desigur, întotdeauna o fracțiune din șansele de a obține un 1, 2, 3 sau 4.
pentru un exemplu de variabilă aleatoare continuă, următoarea applet arată CDF distribuit în mod normal.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Pur și simplu rețineți că caracteristicile unui CDF descrise mai sus și explicate pentru o variabilă aleatoare discretă dețin și pentru variabile aleatorii continue.
pentru exemple mai intuitive ale proprietăților CDF-urilor, consultați exemplul interactiv de mai jos. De asemenea, parcelele interactive ale multor alte CDF-uri importante pentru domeniul statisticilor și utilizate pe acest site pot fi găsite aici.
Funcții de Densitate de Probabilitate (PDF):
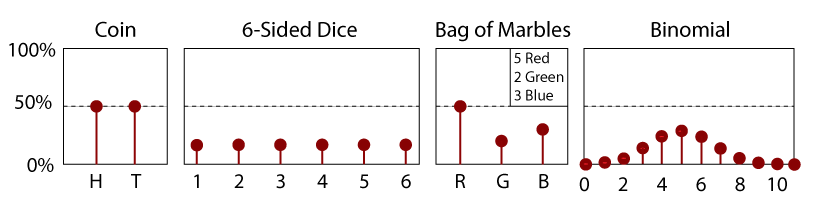
PDF pentru un Târg 6-Sidded Zaruri.
un PDF este pur și simplu derivatul unui CDF., Astfel, un PDF este, de asemenea, o funcție a unei variabile aleatoare, x, iar magnitudinea sa va fi o indicație a probabilității relative de măsurare a unei anumite valori. Deoarece este panta unui CDF, un PDF trebuie să fie întotdeauna pozitiv; nu există cote negative pentru niciun eveniment. În plus, prin definiție, aria de sub curba reprezentând un PDF(x) între -∞ și x este egală cu CDF(x). Ca atare, zona dintre două valori x1 și x2 dă probabilitatea de a măsura o valoare în acest interval.
următorul applet arată un exemplu de PDF pentru o variabilă aleatoare distribuită în mod normal, x.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., de asemenea, luați în considerare diferența dintre un PDF continuu și discret. În timp ce un PDF discret (cum ar fi cel arătat mai sus pentru zaruri) vă va oferi șansele de a obține un anumit rezultat, probabilitățile cu PDF-uri continue sunt chestiuni de gamă, Nu puncte discrete. De exemplu, există în mod clar o șansă de 1 în 6 (16,6%) de a rula un 3 pe un zar, așa cum se poate vedea în PDF-ul său. Dar care sunt ciudat de măsurare exact zero, cu o variabilă aleatoare având un PDF normal și medie de zero, așa cum se arată mai sus? Chiar dacă este valoarea în care PDF-ul este cel mai mare, șansa de a măsura exact 0.00000..,. este, poate contra intuitiv, zero. Șansele de a măsura un anumit număr aleatoriu la o precizie infinită sunt, de fapt, zero. cu un PDF continuu, puteți întreba în schimb care sunt șansele pe care le veți măsura între două valori pentru a obține o probabilitate mai mare decât zero. Pentru a găsi această probabilitate, folosim pur și simplu CDF-ul variabilei noastre aleatorii., Deoarece CDF ne spune cota măsurării unei valori sau ceva mai mic decât acea valoare, pentru a găsi probabilitatea măsurării între două valori, x1 și x2 (unde x1 > x2), trebuie doar să luăm valoarea CDF la x1 și să scădem din ea valoarea CDF la x2. De exemplu, folosind normal CDF în applet-ul de mai sus (cu μ=0, σ=1), dacă am dori să știm care sunt șansele de măsurare între 0,01 și 0,02 găsim CDF(x=0.1)=53.9828% și CDF(x=0.2)=57.9260%. Apoi diferența, CDF(0.2) – CDF(0.1), ne oferă cotele de aproximativ 3.9% din măsurarea unui x între 0.1 și 0.2., pentru exemple mai intuitive, vizuale ale proprietăților PDF-urilor, consultați exemplul interactiv de mai jos. De asemenea, parcelele interactive ale multor PDF-uri importante utilizate pe acest site pot fi văzute aici. |
|||||||||||||||||