Définitions de Statistique > ANOVA
Contenu:
- Le Test ANOVA
- Une ANOVA
- Deux ANOVA
- qu’est-Ce que MANOVA?
- Qu’est-ce que L’ANOVA factorielle?
- Comment exécuter un test ANOVA
- Anova vs. T
- mesures répétées ANOVA
- sphéricité
le Test ANOVA
qu’est-ce que L’ANOVA?, Regardez la vidéo pour une introduction, ou lisez la suite ci-dessous:
Vous avez toujours des problèmes? Chegg.com vous correspondra avec un tuteur (votre première leçon est gratuite!).
un test ANOVA est un moyen de savoir si les résultats d’une enquête ou d’une expérience sont significatifs. En d’autres termes, ils vous aident à déterminer si vous devez rejeter l’hypothèse nulle ou accepter l’hypothèse alternative.
fondamentalement, vous testez des groupes pour voir s’il y a une différence entre eux., Exemples de cas où vous pourriez vouloir tester différents groupes:
- Un groupe de patients psychiatriques essaie trois thérapies différentes: le counseling, les médicaments et le biofeedback. Vous voulez voir si une thérapie est meilleure que les autres.
- Un fabricant a deux processus différents pour fabriquer des ampoules. Ils veulent savoir si un processus est meilleur que l’autre.
- Les étudiants de différents collèges passent le même examen. Vous voulez voir si un collège surpasse l’autre.
que signifie « unidirectionnel” ou « bidirectionnel?,
unidirectionnel ou bidirectionnel fait référence au nombre de variables indépendantes (IVs) dans votre test D’analyse de Variance.
- unidirectionnel a une variable indépendante (avec 2 niveaux). Par exemple: marque de céréales,
- deux voies a deux variables indépendantes (il peut avoir plusieurs niveaux). Par exemple: marque de céréales, calories.
que sont les « groupes » ou les”niveaux »?
Les groupes ou niveaux sont des groupes différents au sein d’une même variable indépendante. Dans l’exemple ci — dessus, vos niveaux pour « brand of cereal” pourraient être Lucky Charms, Raisin Bran, Cornflakes-un total de trois niveaux., Vos niveaux de « Calories » pourraient être: sucré, non sucré — un total de deux niveaux.
disons que vous étudiez si un groupe de soutien alcoolique et un conseil individuel combinés sont le traitement le plus efficace pour réduire la consommation d’alcool. Vous pouvez diviser les participants à l’étude en trois groupes ou niveaux:
- médicaments uniquement,
- médicaments et conseils,
- conseils uniquement.
Ta variable dépendante serait le nombre de boissons alcoolisées consommées par jour.,
Si vos groupes ou niveaux ont une structure hiérarchique (chaque niveau a des sous-groupes uniques), utilisez une ANOVA imbriquée pour l’analyse.
que signifie « réplication”?
c’est si vous répliquez (c’est-à-dire Dupliquez) vos tests avec plusieurs groupes. Avec une ANOVA bidirectionnelle avec réplication, vous avez deux groupes et les individus de ce groupe font plus d’une chose (c’est-à-dire deux groupes d’étudiants de deux collèges qui passent deux tests). Si vous n’avez qu’un seul groupe prenant deux tests, vous utiliseriez sans réplication.
types de Tests.,
Il existe deux types principaux: unidirectionnel et bidirectionnel. Les tests bidirectionnels peuvent être avec ou sans réplication.
- ANOVA unidirectionnelle entre groupes: utilisée lorsque vous souhaitez tester deux groupes pour voir s’il y a une différence entre eux.
- ANOVA bidirectionnelle sans réplication: utilisée lorsque vous avez un groupe et que vous testez deux fois ce même groupe. Par exemple, vous testez un ensemble de personnes avant et après qu’elles prennent un médicament pour voir si cela fonctionne ou non.
- ANOVA bidirectionnelle avec réplication: deux groupes, et les membres de ces groupes font plus d’une chose., Par exemple, deux groupes de patients de différents hôpitaux essayant deux thérapies différentes.
retour en haut
ANOVA à Sens Unique
une ANOVA à Sens Unique est utilisée pour comparer deux moyennes de deux groupes indépendants (non liés) en utilisant la distribution F. L’hypothèse nulle pour le test est que les deux moyennes sont égales. Par conséquent, un résultat significatif signifie que les deux moyens sont inégaux.
exemples d’utilisation d’une ANOVA à Sens Unique
Situation 1: vous avez un groupe d’individus divisé au hasard en groupes plus petits et accomplissant différentes tâches., Par exemple, vous pourriez étudier les effets du thé sur la perte de poids et former trois groupes: le thé vert, le thé noir et pas de thé.
Situation 2: semblable à la situation 1, mais dans ce cas, les individus sont divisés en groupes en fonction d’un attribut qu’ils possèdent. Par exemple, vous pourriez étudier la force des jambes des personnes en fonction du poids. Vous pouvez diviser les participants en catégories de poids (obèses, en surpoids et normaux) et mesurer la force de leurs jambes sur une machine de musculation.,
Limitations de L’ANOVA à Sens Unique
une ANOVA à Sens Unique vous dira qu’au moins deux groupes étaient différents l’un de l’autre. Mais il ne vous dira pas quels groupes étaient différents. Si votre test renvoie une statistique F significative, vous devrez peut-être exécuter un test ad hoc (comme le test de différence la moins significative) pour vous dire exactement quels groupes avaient une différence de moyenne.
retour en haut
Anova bidirectionnelle
une ANOVA bidirectionnelle est une extension de l’ANOVA à Sens Unique. Avec un sens unique, vous avez une variable indépendante affectant une variable dépendante., Avec une ANOVA bidirectionnelle, il y a deux indépendants. Utilisez une ANOVA bidirectionnelle lorsque vous avez une variable de mesure (c’est-à-dire une variable quantitative) et deux variables nominales. En d’autres termes, si votre expérience a un résultat quantitatif et que vous avez deux variables explicatives catégorielles, une ANOVA bidirectionnelle est appropriée.
par exemple, vous voudrez peut-être savoir s’il existe une interaction entre le revenu et le sexe pour le niveau d’anxiété lors des entretiens d’embauche. Le niveau d’anxiété est le résultat, ou la variable qui peut être mesuré. Le sexe et le revenu sont les deux variables catégorielles., Ces variables catégorielles sont également les variables indépendantes, appelées facteurs dans une ANOVA bidirectionnelle.
Les facteurs peuvent être divisés en niveaux. Dans l’exemple ci-dessus, le niveau de revenu pourrait être divisé en trois niveaux: faible, moyen et élevé. Le genre pourrait être divisé en trois niveaux: homme, femme et transgenre. Les groupes de traitement sont toutes les combinaisons possibles des facteurs. Dans cet exemple, il y aurait 3 x 3 = 9 groupes de traitement.
Effet Principal et l’Effet d’Interaction
Les résultats de Deux ANOVA calculera un effet principal et un effet d’interaction., L’effet principal est similaire à une ANOVA à Sens Unique: l’effet de chaque facteur est considéré séparément. Avec l’effet d’interaction, tous les facteurs sont considérés en même temps. Les effets d’Interaction entre les facteurs sont plus faciles à tester s’il y a plus d’une observation dans chaque cellule. Pour l’exemple ci-dessus, plusieurs scores de stress pourraient être entrés dans les cellules. Si vous entrez plusieurs observations dans les cellules, le nombre dans chaque cellule doit être égale.
Deux hypothèses nulles sont testés si vous placez une observation dans chaque cellule., Pour cet exemple, ces hypothèses seraient:
H01: tous les groupes de revenus ont un stress moyen égal.
H02: tous les groupes de genre ont un stress moyen égal.
pour des observations multiples dans des cellules, vous testeriez également une troisième hypothèse:
H03: les facteurs sont indépendants ou l’effet d’interaction n’existe pas.
une statistique F est calculée pour chaque hypothèse que vous testez.
hypothèses pour L’ANOVA bidirectionnelle
- la population doit être proche d’une distribution normale.
- les Échantillons doivent être indépendants.
- les variances de Population doivent être égales.,
- Les groupes doivent avoir des échantillons de taille égale.
haut de page
QU’est-ce que MANOVA?
MANOVA est juste une ANOVA avec plusieurs variables dépendantes. Il est similaire à de nombreux autres tests et expériences en ce sens que son but est de savoir si la variable de réponse (c’est-à-dire votre variable dépendante) est modifiée en manipulant la variable indépendante. Le test permet de répondre à de nombreuses questions de recherche, notamment:
- Les changements apportés aux variables indépendantes ont-ils des effets statistiquement significatifs sur les variables dépendantes?
- Quelles sont les interactions entre les variables dépendantes?,
- quelles sont les interactions entre variables indépendantes?
exemple de MANOVA
supposons que vous vouliez savoir si une différence dans les manuels affectait les scores des élèves en mathématiques et en sciences. Les améliorations en mathématiques et en sciences signifient qu’il y a deux variables dépendantes, donc une MANOVA est appropriée.
une ANOVA vous donnera une valeur f unique (univariée) tandis qu’une MANOVA vous donnera une valeur F multivariée. MANOVA teste les variables dépendantes multiples en créant de nouvelles variables dépendantes artificielles qui maximisent les différences de groupe., Ces nouvelles variables dépendantes sont des combinaisons linéaires des variables dépendantes mesurées.
interprétation des résultats de MANOVA
Si la valeur F multivariée indique que le test est statistiquement significatif, cela signifie que quelque chose est significatif. Dans l’exemple ci-dessus, vous ne sauriez pas si les scores en mathématiques se sont améliorés, les scores en sciences se sont améliorés (ou les deux)., Une fois que vous avez un résultat significatif, vous devrez alors regarder chaque composant individuel (les tests F univariés) pour voir quelle(S) variable (s) dépendante (s) a contribué au résultat statistiquement significatif.
avantages et inconvénients de MANOVA vs ANOVA
avantages
- MANOVA vous permet de tester plusieurs variables dépendantes.
- MANOVA peut protéger contre les erreurs de Type I.
inconvénients
- MANOVA est beaucoup plus compliqué que ANOVA, ce qui rend difficile de voir quelles variables indépendantes affectent les variables dépendantes.,
- Un degré de liberté est perdue avec l’ajout de chaque nouvelle variable.
- Les variables dépendantes doivent être non corrélées autant que possible. S’ils sont corrélés, la perte de degrés de liberté signifie qu’il n’y a pas beaucoup d’avantages à inclure plus d’une variable dépendante sur le test.
référence:
(SFSU)
retour en haut
Qu’est-ce que L’ANOVA factorielle?
une ANOVA factorielle est une analyse de test de Variance avec plus d’une variable indépendante, ou « facteur ». Il peut également faire référence à plus d’un niveau de Variable indépendante., Par exemple, une expérience avec un groupe de traitement et groupe de contrôle est un facteur (le traitement) mais à deux niveaux (le traitement et le contrôle). Les termes « deux” et « trois” se réfèrent au nombre de facteurs ou le nombre de niveaux dans votre test. Les ANOVA à quatre voies et au-dessus sont rarement utilisées car les résultats du test sont complexes et difficiles à interpréter.
- une ANOVA bidirectionnelle a deux facteurs (variables indépendantes) et une variable dépendante. Par exemple, le temps passé à étudier et les connaissances préalables sont des facteurs qui influent sur votre réussite à un test.,
- une ANOVA à trois voies a trois facteurs (variables indépendantes) et une variable dépendante. Par exemple, le temps passé à étudier, les connaissances préalables et les heures de sommeil sont des facteurs qui affectent votre efficacité lors d’un test
L’ANOVA factorielle est un moyen efficace de réaliser un test. Au lieu d’effectuer une série d’expériences où vous testez une variable indépendante contre une variable dépendante, vous pouvez tester toutes les variables indépendantes en même temps.
variabilité
dans une ANOVA à Sens Unique, la variabilité est due aux différences entre les groupes et les différences au sein des groupes., Dans l’ANOVA factorielle, chaque niveau et facteur sont appariés les uns avec les autres (« croisés”). Cela vous aide à voir quelles interactions se déroulent entre les niveaux et les facteurs. S’il y a une interaction, les différences dans un facteur dépendent des différences dans un autre.
supposons que vous utilisiez une ANOVA bidirectionnelle pour tester la performance masculine / féminine lors d’un examen final. Les sujets avaient eu 4, 6 ou 8 heures de sommeil.,
- IV1: sexe (Homme/Femme)
- IV2: sommeil (4/6/8)
- DV: Score final à L’examen
une ANOVA factorielle bidirectionnelle vous aiderait à répondre aux questions suivantes:
- Le sexe est-il un effet principal? En d’autres termes, les hommes et les femmes diffèrent-ils considérablement sur leurs performances à l’examen?
- Le sommeil est-il un effet principal? En d’autres termes, les personnes qui ont eu 4,6 ou 8 heures de sommeil diffèrent-elles considérablement dans leurs performances?
- Est-il une interaction significative entre les facteurs? En d’autres termes, comment les heures de sommeil et le sexe interagissent-ils en ce qui concerne les performances des examens?,
- peut-on trouver des différences de sexe et de performance aux examens dans les différents niveaux de sommeil?
hypothèses D’ANOVA factorielle
- normalité: la variable dépendante est normalement distribuée.
- indépendance: les Observations et les groupes sont indépendants les uns des autres.
- égalité de la Variance: les variances de la population sont égales entre les facteurs / niveaux.
comment exécuter une ANOVA
ces tests prennent beaucoup de temps à la main. Dans presque tous les cas, vous voudrez utiliser un logiciel., Par exemple, plusieurs options sont disponibles dans Excel:
- Anova bidirectionnelle dans Excel avec réplication et sans réplication.
- ANOVA à Sens Unique dans Excel 2013.
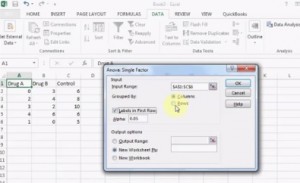
l’Exécution de l’essai dans Excel.
Les tests ANOVA dans les paquets de statistiques sont exécutés sur des données paramétriques. Si vous avez des données de rang ou ordonnées, vous voudrez exécuter une ANOVA non paramétrique (généralement trouvée sous une rubrique différente dans le Logiciel, comme « tests non paramétriques »).,
étapes
Il est peu probable que vous souhaitiez faire ce test à la main, mais si vous le devez, voici les étapes à suivre:
- trouvez la moyenne pour chacun des groupes.
- trouver la moyenne globale (la moyenne des groupes combinés).
- trouver la Variation dans le groupe; l’écart total du score de chaque membre par rapport à la moyenne du groupe.
- trouver la Variation entre groupes: l’écart de chaque moyenne de groupe par rapport à la moyenne globale.
- trouver la statistique F: le rapport entre la Variation du groupe et la Variation à l’intérieur du groupe.
ANOVA vs, T Test
Le T-test D’un étudiant vous indiquera s’il existe une variation significative entre les groupes. Un test t compare les moyennes, tandis que L’ANOVA compare les variances entre les populations.
Vous pouvez techniquement effectuer une série de T-tests sur vos données. Cependant, comme les groupes de croître en nombre, vous pouvez vous retrouver avec beaucoup de paires de comparaisons que vous devez exécuter. ANOVA vous donnera un seul nombre (la statistique f) et une valeur p pour vous aider à soutenir ou à rejeter l’hypothèse nulle.,
retour en haut
Repeated Measures ANOVA
A repeated measures ANOVA est presque la même que L’ANOVA unidirectionnelle, avec une différence principale: vous testez des groupes liés, pas des groupes indépendants. C’est ce qu’on appelle des mesures répétées parce que le même groupe de participants est mesuré encore et encore. Par exemple, vous pourriez étudier les niveaux de cholestérol du même groupe de patients à 1, 3 et 6 mois après avoir changé leur régime alimentaire. Pour cet exemple, la variable indépendante est » temps « et la variable dépendante est » cholestérol.,” La variable indépendante est généralement appelée le facteur intra-sujets.
mesures répétées ANOVA est similaire à une conception multivariée simple. Dans les deux tests, les mêmes participants sont mesurés encore et encore. Cependant, avec des mesures répétées, la même caractéristique est mesurée avec une condition différente. Par exemple, la pression artérielle est mesurée sur la condition « temps”. Pour une conception multivariée simple, c’est la caractéristique qui change. Par exemple, vous pouvez mesurer la pression artérielle, la fréquence cardiaque et la fréquence respiratoire au cours du temps.,
raisons d’utiliser des mesures répétées ANOVA
- lorsque vous collectez des données auprès des mêmes participants sur une période de temps, les différences individuelles (une source de différences entre les groupes) sont réduites ou éliminées.
- Les tests sont plus puissants car la taille de l’échantillon n’est pas divisée entre les groupes.
- Le test peut être économique, car vous utilisez les mêmes participants.,
hypothèses pour les mesures répétées ANOVA
les résultats de vos mesures répétées ANOVA ne seront valables que si les hypothèses suivantes n’ont pas été violées:
- Il doit y avoir une variable indépendante et une variable dépendante.
- La variable dépendante doit être une variable continue, sur une échelle d’intervalles ou d’un rapport d’échelle.
- la variable indépendante doit être catégorique, soit sur l’échelle nominale, soit sur l’échelle ordinale.
- idéalement, les niveaux de dépendance entre paires de groupes sont égaux (« sphéricité”)., Des Corrections sont possibles si cette hypothèse est violée.
mesures répétées ANOVA dans SPSS: étapes
Étape 1: Cliquez sur « Analyser”, puis survolez « modèle linéaire général. »Cliquez » Mesures Répétées. »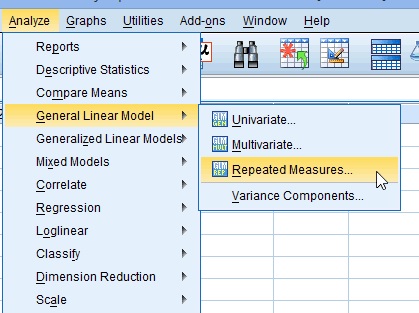
Étape 2: Remplacez le nom” factor1 » par quelque chose qui représente votre variable indépendante. Par exemple, vous pouvez mettre « âge” ou « temps.”
Étape 3: Entrez le Nombre de Niveaux.” C’est combien de fois la variable dépendante a été mesurée. Par exemple, si vous avez pris des mesures chaque semaine pendant un total de 4 semaines, ce nombre serait de 4.,
Étape 4: Cliquez sur le bouton” Ajouter », puis donnez un nom à votre variable dépendante.
Étape 5: Cliquez sur le bouton” Ajouter ». Une boîte de définition de mesures répétées apparaîtra. Cliquez sur le bouton « Définir” bouton.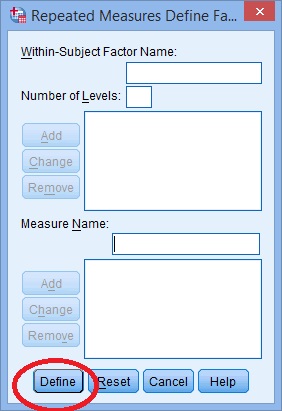
Étape 6: Utilisez les touches fléchées pour déplacer vos variables de gauche à droite afin que votre écran ressemble à l’image ci-dessous: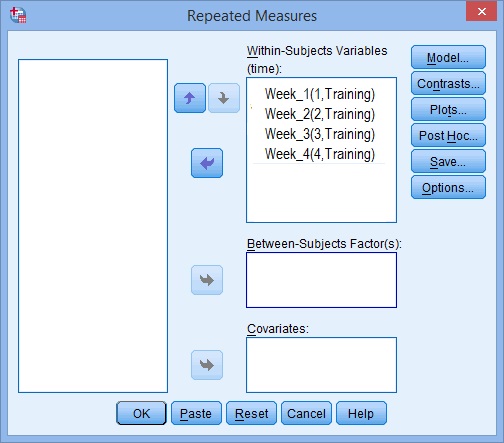
Étape 7: Cliquez sur « tracés” et utilisez les touches fléchées pour transférer le facteur de la boîte de gauche sur la boîte D’axe Horizontal.
Étape 8: Cliquez sur » Ajouter « puis sur” Continuer » en bas de la fenêtre.,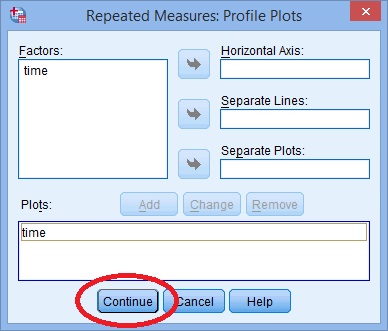
Étape 9: Cliquez sur « Options », puis transférez vos facteurs de la boîte de gauche vers les moyens D’affichage de la boîte de droite.
Étape 10: Cochez les cases suivantes:
- comparer les effets principaux.
- Statistiques Descriptives.
- estimations de la taille de l’effet.
étape 11: sélectionnez « Bonferroni” dans le menu déroulant sous Réglage de L’Intervalle de confiance.
Etape 12: Cliquez sur « Continuer” puis cliquez sur « OK” pour exécuter le test.,
haut de page
sphéricité
en statistique, la sphéricité (ε) fait référence au test de sphéricité de Mauchly, qui a été développé en 1940 par John W. Mauchly, qui a co-développé le premier ordinateur électronique à usage général.
définition
la sphéricité est utilisée comme hypothèse dans les mesures répétées ANOVA. L’hypothèse stipule que les variances des différences entre toutes les paires de groupes possibles sont égales. Si vos données violent cette hypothèse, cela peut entraîner une augmentation d’une erreur de Type I (le rejet incorrect de l’hypothèse nulle).,
Il est très fréquent que des mesures répétées ANOVA entraînent une violation de l’hypothèse. Si l’hypothèse a été violée, des corrections ont été élaborées pour éviter une augmentation du taux d’erreur de type I. La correction est appliquée aux degrés de liberté dans la distribution F.
Test de sphéricité de Mauchly
Le test de sphéricité de Mauchly peut être exécuté dans la majorité des logiciels statistiques, où il a tendance à être le test par défaut de sphéricité. Le test de Mauchly est idéal pour les échantillons de taille moyenne., Il peut ne pas détecter la sphéricité dans de petits échantillons et il peut sur-Détecter dans de grands échantillons.
Si le test renvoie une petite valeur p (p ≤.05), ceci est une indication que vos données ont violé l’hypothèse. L’image suivante de la sortie SPSS pour ANOVA montre que la signification « sig” attachée à celle de Mauchly est .274. Cela signifie que l’hypothèse n’a pas été violé pour cet ensemble de données.
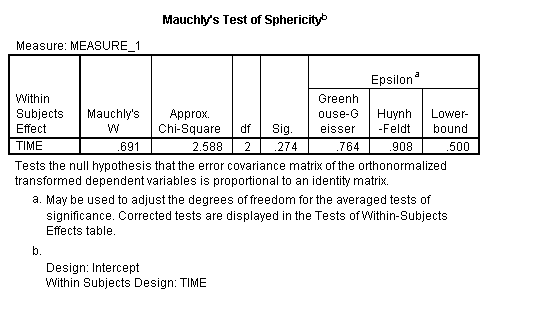
Image: UVM.,EDU
Vous rapporteriez le résultat ci-dessus comme « le Test de Mauchly a indiqué que l’hypothèse de sphéricité n’avait pas été violée, χ2(2) = 2.588, p = .274. »
Si votre test a renvoyé une petite valeur p, Vous devez appliquer une correction, généralement soit la correction:
- Greehouse-Geisser.
- Huynh-Feldt de correction.
lorsque ε ≤ 0,75 (ou si vous ne savez pas quelle est la valeur de la statistique), utilisez la correction de Greenhouse-Geisser.
quand ε >.75, utilisez la correction de Huynh-Feldt.,
Retour en Haut
moyenne
ANOVA vs Régression
——————————————————————————
Besoin d’aide avec les devoirs à faire ou une question du test? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions d’un expert dans le domaine. Vos 30 premières minutes avec un tuteur Chegg sont gratuites!